Difference between revisions of "Aufgaben:Exercise 3.11Z: Metric and Accumutated Metric"
m (Guenter verschob die Seite 3.11Z Maximum-Likelihood-Fehlergrößen nach 3.11Z Maximum-Likelihood-Fehlergrößen) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID1476__Dig_Z_3_11.png|right|frame|Berechnung der minimalen Gesamtfehlergrößen]] | [[File:P_ID1476__Dig_Z_3_11.png|right|frame|Berechnung der minimalen Gesamtfehlergrößen]] | ||
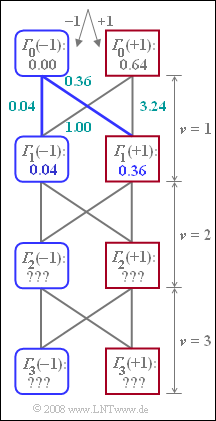
| − | Für die in der [[Aufgaben:3.11_Viterbi-Empf%C3%A4nger_und_Trellisdiagramm|Aufgabe | + | Für die in der [[Aufgaben:3.11_Viterbi-Empf%C3%A4nger_und_Trellisdiagramm|Aufgabe 3.11]] behandelte Maximum–Likelihood–Konstellation mit bipolaren Amplitudenkoeffizient $a_{\rm \nu} ∈ \{+1, –1\}$ sollen die Fehlergrößen $\varepsilon_{\rm \nu}(i)$ sowie die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(–1)$ und ${\it \Gamma}_{\rm \nu}(+1)$ ermittelt werden. |
| − | Der Grundimpuls ist durch die beiden Werte $g_0$ und $g_{\rm –1}$ gegeben. Diese können ebenso wie die Detektionsabtastwerte $d_0$ und $d_1$ aus den nachfolgenden Berechnungen für die Fehlergrößen $\ | + | Der Grundimpuls ist durch die beiden Werte $g_0$ und $g_{\rm –1}$ gegeben. Diese können ebenso wie die Detektionsabtastwerte $d_0$ und $d_1$ aus den nachfolgenden Berechnungen für die Fehlergrößen $\varepsilon_{\rm \nu}(i)$ zu den Zeitpunkten $\nu = 0$ und $\nu = 1$ entnommen werden. Anzumerken ist, dass vor der eigentlichen Nachricht ($a_1$, $a_2$, $a_3$) stets das Symbol $a_0 = 0$ gesendet wird. Für den Zeitpunkt $\nu = 0$ gilt: |
:$$\varepsilon_{0}(+1) \ = \ [-0.4- 0.4]^2=0.64 \hspace{0.05cm},$$ | :$$\varepsilon_{0}(+1) \ = \ [-0.4- 0.4]^2=0.64 \hspace{0.05cm},$$ | ||
:$$\varepsilon_{0}(-1) \ = \ [-0.4+ 0.4]^2=0.00 \hspace{0.05cm}.$$ | :$$\varepsilon_{0}(-1) \ = \ [-0.4+ 0.4]^2=0.00 \hspace{0.05cm}.$$ | ||
| − | Daraus könnte bereits zum Zeitpunkt $\nu = 0$ geschlossen werden, dass mit großer Wahrscheinlichkeit $a_1 = \ | + | Daraus könnte bereits zum Zeitpunkt $\nu = 0$ geschlossen werden, dass mit großer Wahrscheinlichkeit $a_1 = -\hspace{-0.05cm}1$ ist. Für den Zeitpunkt $\nu = 1$ ergeben sich folgende Fehlergrößen: |
:$$\varepsilon_{1}(+1, +1) \ = \ [-0.8- 0.6 -0.4]^2=3.24 | :$$\varepsilon_{1}(+1, +1) \ = \ [-0.8- 0.6 -0.4]^2=3.24 | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 19: | Line 19: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}( | + | Die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(-\hspace{-0.07cm}1)$ und ${\it \Gamma}_{\rm \nu}(+1)$, die mit diesen sechs Fehlergrößen berechnet werden können, sind bereits in der Grafik eingezeichnet. Die weiteren Detektionsabtastwerte sind |
:$$d_{2}=0.1 \hspace{0.05cm},\hspace{0.2cm} | :$$d_{2}=0.1 \hspace{0.05cm},\hspace{0.2cm} | ||
d_{3}=0.5 \hspace{0.05cm}.$$ | d_{3}=0.5 \hspace{0.05cm}.$$ | ||
| − | ''Hinweise:'' | + | |
| − | * Die Aufgabe gehört zum | + | ''Hinweise:'' |
| − | * Alle Größen sind hier normiert zu verstehen. | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Viterbi%E2%80%93Empf%C3%A4nger|Viterbi–Empfänger]]. |
| − | * Die | + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. |
| + | * Alle Größen sind hier normiert zu verstehen. Gehen Sie izudem von biipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus: ${\rm Pr} (a_\nu = -\hspace{-0.05cm}1) = {\rm Pr} (a_\nu = +1)= 0.5.$ | ||
| + | * Die Thematik wird auch im Interaktionsmodul [[Eigenschaften des Viterbi–Empfängers]] behandelt. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Von welchen Detektionsabtastwerten $d_0$ und $d_1$ wurde ausgegangen? | + | {Von welchen Detektionsabtastwerten $d_0$ und $d_1$ wurde hier ausgegangen? |
|type="{}"} | |type="{}"} | ||
| − | $d_0$ | + | $d_0 \ = \ $ { -0.412--0.388 } |
| − | $d_1$ | + | $d_1\ = \ $ { -0.824--0.776 } |
{Welche Grundimpulswerte wurden dabei vorausgesetzt? | {Welche Grundimpulswerte wurden dabei vorausgesetzt? | ||
|type="{}"} | |type="{}"} | ||
| − | $g_0$ | + | $g_0\ = \ $ { +0.6 3% } |
| − | $g_{ | + | $g_{-1} \ = \ $ { +0.4 3% } |
{Welche der aufgeführten Detektionsabtastwerte sind für $\nu ≥ 1$ möglich? | {Welche der aufgeführten Detektionsabtastwerte sind für $\nu ≥ 1$ möglich? | ||
| Line 48: | Line 51: | ||
+ $±1.0.$ | + $±1.0.$ | ||
| − | { | + | {Geben Sie die minimalen Gesamtfehlergrößen für die Zeit $\nu = 2$ an $(d_2 = 0.1)$. |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Gamma}_2(+1)$ | + | ${\it \Gamma}_2(+1)\ = \ $ { 0.13 3% } |
| − | ${\it \Gamma}_2( | + | ${\it \Gamma}_2(-\hspace{-0.05cm}1)\ = \ $ { 0.37 3% } |
| − | {Berechnen Sie die minimalen Gesamtfehlergrößen für die Zeit $\nu = 3$ ( | + | {Berechnen Sie die minimalen Gesamtfehlergrößen für die Zeit $\nu = 3$ $(d_3 = 0.5)$. |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_3(+1)$ = { 0.38 3% } | ${\it \Gamma}_3(+1)$ = { 0.38 3% } | ||
| − | ${\it \Gamma}_3( | + | ${\it \Gamma}_3(-\hspace{-0.05cm}1)$ = { 0.22 3% } |
</quiz> | </quiz> | ||
Revision as of 14:23, 3 November 2017
Für die in der Aufgabe 3.11 behandelte Maximum–Likelihood–Konstellation mit bipolaren Amplitudenkoeffizient $a_{\rm \nu} ∈ \{+1, –1\}$ sollen die Fehlergrößen $\varepsilon_{\rm \nu}(i)$ sowie die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(–1)$ und ${\it \Gamma}_{\rm \nu}(+1)$ ermittelt werden.
Der Grundimpuls ist durch die beiden Werte $g_0$ und $g_{\rm –1}$ gegeben. Diese können ebenso wie die Detektionsabtastwerte $d_0$ und $d_1$ aus den nachfolgenden Berechnungen für die Fehlergrößen $\varepsilon_{\rm \nu}(i)$ zu den Zeitpunkten $\nu = 0$ und $\nu = 1$ entnommen werden. Anzumerken ist, dass vor der eigentlichen Nachricht ($a_1$, $a_2$, $a_3$) stets das Symbol $a_0 = 0$ gesendet wird. Für den Zeitpunkt $\nu = 0$ gilt:
- $$\varepsilon_{0}(+1) \ = \ [-0.4- 0.4]^2=0.64 \hspace{0.05cm},$$
- $$\varepsilon_{0}(-1) \ = \ [-0.4+ 0.4]^2=0.00 \hspace{0.05cm}.$$
Daraus könnte bereits zum Zeitpunkt $\nu = 0$ geschlossen werden, dass mit großer Wahrscheinlichkeit $a_1 = -\hspace{-0.05cm}1$ ist. Für den Zeitpunkt $\nu = 1$ ergeben sich folgende Fehlergrößen:
- $$\varepsilon_{1}(+1, +1) \ = \ [-0.8- 0.6 -0.4]^2=3.24 \hspace{0.05cm},$$
- $$\varepsilon_{1}(+1, -1) \ = \ [-0.8- 0.6 +0.4]^2=1.00 \hspace{0.05cm},$$
- $$\varepsilon_{1}(-1, +1) \ = \ [-0.8+ 0.6 -0.4]^2=0.36 \hspace{0.05cm},$$
- $$ \varepsilon_{1}(-1, -1) \ = \ [-0.8+ 0.6 +0.4]^2=0.04 \hspace{0.05cm}.$$
Die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(-\hspace{-0.07cm}1)$ und ${\it \Gamma}_{\rm \nu}(+1)$, die mit diesen sechs Fehlergrößen berechnet werden können, sind bereits in der Grafik eingezeichnet. Die weiteren Detektionsabtastwerte sind
- $$d_{2}=0.1 \hspace{0.05cm},\hspace{0.2cm} d_{3}=0.5 \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Viterbi–Empfänger.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Alle Größen sind hier normiert zu verstehen. Gehen Sie izudem von biipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus: ${\rm Pr} (a_\nu = -\hspace{-0.05cm}1) = {\rm Pr} (a_\nu = +1)= 0.5.$
- Die Thematik wird auch im Interaktionsmodul Eigenschaften des Viterbi–Empfängers behandelt.
Fragebogen
Musterlösung
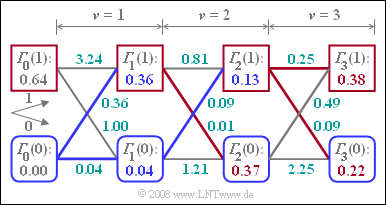
(2) Die Fehlergrößen $\epsilon_0(i)$ beinhalten den Grundimpulswert $g_{\rm –1}$, über den der Zusammenhang zwischen dem Amplitudenkoeffizienten $a_1$ und dem Detektionsabtastwert $d_0$ hergestellt wird ($g_0$ ist in diesen Gleichungen nicht enthalten). Man erkennt $g_{\rm –1} \underline {= 0.4}$. Aus den Gleichungen für $\nu = 1$ ist der Hauptwert $g_0 \underline {= 0.6}$ ablesbar.
(3) Die möglichen Nutzabtastwerte sind $±g_0 ±g_{\rm –1} = ±0.6 ±0.4$, also $\underline {±0.2}$ und $\underline {±1.0}$. Bei unipolarer Signalisierung würden sich die Werte $0, \ 0.4, \ 0.6$ und $1$ ergeben. Der Zusammenhang zwischen bipolaren Werten $b_i$ und den unipolaren Äquivalenten $u_i$ lautet allgemein:
- $$b_i = 2 \cdot u_i - 1 \hspace{0.05cm}.$$
(4) Die Fehlergrößen ergeben sich für $\nu = 2$ unter Berücksichtigung des Ergebnisses aus (3) wie folgt:
- $$\varepsilon_{2}(+1, +1) \ = \ [0.1 - 1.0]^2=0.81,\hspace{0.2cm} \varepsilon_{2}(-1, +1) = [0.1 +0.2]^2=0.09 \hspace{0.05cm},$$
- $$\varepsilon_{2}(+1, -1) \ = \ [0.1 -0.2]^2=0.01,\hspace{0.2cm} \varepsilon_{2}(-1, -1) = [0.1 +1.0]^2=1.21 \hspace{0.05cm}.$$
Damit lauten die minimalen Gesamtfehlergrößen:
- $${\it \Gamma}_{2}(+1) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(+1) + \varepsilon_{2}(+1, +1), \hspace{0.2cm}{\it \Gamma}_{1}(-1) + \varepsilon_{2}(-1, +1)\right] = $$
- $$\ = \ {\rm Min}\left[0.36 + 0.81, 0.04 + 0.09\right]\hspace{0.15cm}\underline {= 0.13} \hspace{0.05cm},$$
- $${\it \Gamma}_{2}(-1) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(+1) + \varepsilon_{2}(+1, -1), \hspace{0.2cm}{\it \Gamma}_{1}(-1) + \varepsilon_{2}(-1, -1)\right] =$$
- $$\ = \ {\rm Min}\left[0.36 + 0.01, 0.04 + 1.21\right]\hspace{0.15cm}\underline {= 0.37} \hspace{0.05cm}.$$
${\it \Gamma}_2(+1) = 0.13$ ist die minimale Gesamtfehlergröße unter der Hypothese, dass das nachfolgende Symbol $a_3 = +1$ sein wird. Unter dieser Annahme ist $a_2 = \ –1$ wahrscheinlicher als $a_2 = +1$, wie aus dem nachfolgenden Trellisdiagramm hervorgeht (der ankommende Pfad ist blau).
Hinweis: In obenstehender Grafik ist der Zustand „$1$” als „$+1$” und „$0$” als „$–1$” zu interpretieren.
Eine durchaus realistische Alternative zu der Kombination „$a_2 = \ –1, a_3 = +1$” ist „$a_2 = +1, a_3 = \ –1$”, die zur minimalen Gesamtfehlergröße ${\it \Gamma}_2(–1) = 0.37$ führen. Hier ist der ankommende Pfad rot.
(5) Nun gelten folgende Gleichungen:
- $$\varepsilon_{3}(+1, +1) \ = \ [0.5 - 1.0]^2=0.25,\hspace{0.2cm} \varepsilon_{3}(-1, +1) = [0.5 +0.2]^2=0.49 \hspace{0.05cm},$$
- $$\varepsilon_{3}(+1, -1) \ = \ [0.5 -0.2]^2=0.09,\hspace{0.2cm} \varepsilon_{3}(-1, -1) = [0.5 +1.0]^2=2.25 \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}{\it \Gamma}_{3}(+1) \ = \ {\rm Min}\left[0.13 + 0.25, 0.37 + 0.49\right]\hspace{0.15cm}\underline {= 0.38} \hspace{0.05cm},$$
- $${\it \Gamma}_{3}(-1) \ = \ {\rm Min}\left[0.13 + 0.09, 0.37 + 2.25\right]\hspace{0.15cm}\underline {= 0.22} \hspace{0.05cm}.$$
Bei beiden Gleichungen ist der jeweils erste Term der kleinere, wobei jeweils ${\it \Gamma}_2(+1) = 0.13$ enthalten ist. Deshalb wird der Viterbi–Empfänger mit Sicherheit $a_3 = +1$ ausgeben, ganz egal, welche Informationen er zu späteren Zeitpunkten ($\nu > 3$) noch bekommen wird.
Verfolgt man den durchgehenden Pfad im Trellisdiagramm, so sind durch diese Festlegung bei $\nu = 3$ auch die früheren Amplitudenkoeffizienten fix: $a_1 = a_2 = \ –1$.