Difference between revisions of "Aufgaben:Exercise 4.1Z: Other Basis Functions"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Signale, Basisfunktionen und Vektorräume}} Datei:P_ID1996__Dig_Z_4_1.png|right|frame|Energiebegrenzte Si…“) |
|||
| Line 4: | Line 4: | ||
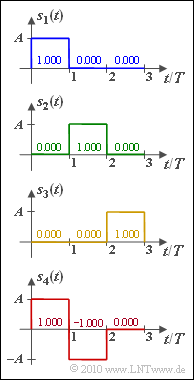
[[File:P_ID1996__Dig_Z_4_1.png|right|frame|Energiebegrenzte Signale]] | [[File:P_ID1996__Dig_Z_4_1.png|right|frame|Energiebegrenzte Signale]] | ||
Diese Aufgabe verfolgt das genau gleiche Ziel wie die [[Aufgaben:4.1_Gram-Schmidt-Verfahren| Aufgabe A4.1]]. Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ ... \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen. | Diese Aufgabe verfolgt das genau gleiche Ziel wie die [[Aufgaben:4.1_Gram-Schmidt-Verfahren| Aufgabe A4.1]]. Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ ... \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen. | ||
| − | :$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} | + | :$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t =\\ |
| − | \hspace{-0.1cm} | + | \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm \delta}_{jk} = |
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
Revision as of 09:24, 4 November 2017
Diese Aufgabe verfolgt das genau gleiche Ziel wie die Aufgabe A4.1. Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ ... \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen.
- $$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t =\\ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} j = k \\ j \ne k \\ \end{array} \hspace{0.05cm}.$$