Aufgaben:Exercise 4.1Z: Other Basis Functions

• Return to book

Energiebegrenzte Signale

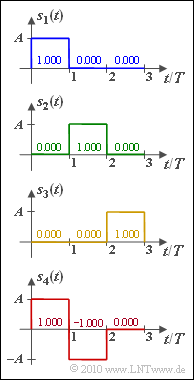
Diese Aufgabe verfolgt das genau gleiche Ziel wie die Aufgabe A4.1. Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ ... \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen.

$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t =\\ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} j = k \\ j \ne k \\ \end{array} \hspace{0.05cm}.$$

Mit $M$ Sendesignale $s_i(t)$ können bereits weniger Basisfunktionen $\varphi_{\it j}(t)$ ausreichen, nämlich $N$. Allgemein gilt also $N ≤ M$.

Es handelt sich hier um die genau gleichen energiebegrenzten Signale $s_i(t)$ wie in der Aufgabe A4.1. Der Unterschied ist die unterschiedliche Reihenfolge der Signale $s_i(t)$. Diese sind in dieser Aufgabe so sortiert, dass die Basisfunktionen auch ohne Anwendung des umständlicheren Gram–Schmidt–Verfahrens gefunden werden können.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Signale, Basisfunktionen und Vektorräume.
• Verwenden Sie für numerische Berechnungen:

$$A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm \mu s} \hspace{0.05cm}. $$

Fragebogen

1

In Aufgabe A4.1 hat das Gram–Schmidt–Verfahren zu $N = 3$ Basisfunktionen geführt. Wieviele Basisfunktionen benötigt man hier?

$N$ =

2

Geben Sie die 2–Norm aller Signale an:

$||s_1(t)||$ = $\ 10^{\rm –3} \ \rm (Ws)^{\rm 0.5} $

3

Multiple-Choice

	correct
	false

4

Input-Box Frage

$xyz$ = $ab$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)