Difference between revisions of "Aufgaben:Exercise 1.5: Cosine-Square Spectrum"
| Line 60: | Line 60: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
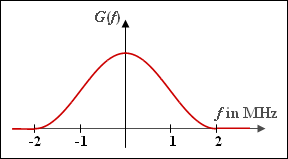
| − | '''(1)''' | + | '''(1)''' Die obere Eckfrequenz kann aus der Grafik abgelesen werden: $f_{2} \underline{= 2 \ \rm MHz}$. Da das Spektrum in keinem Bereich konstant ist, gilt: $f_{1} \underline {= 0}$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' Aus den angegebenen Gleichungen erhält man: | ||
| + | :$$f_{\rm Nyq} = \ \frac{f_1 +f_2 } | ||
| + | {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},$$ | ||
| + | :$$r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(3)''' Der Abstand äquidistanter Nulldurchgänge hängt direkt mit der Nyquistfrequenz zusammen: | ||
| + | :$$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm \mu s}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(4)''' Die erste Aussage ist richtig: Die Funktion $si(π · t/T)$ führt zu Nulldurchgängen bei $\nu T (\nu \neq 0)$. Auch die letzte Aussage trifft zu: Wegen $g(t) = 0$ für $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ wird auch das zweite Nyquistkriterium erfüllt. Falsch ist dagegen die mittlere Aussage, da $g(t = T/2) \neq 0$ ist. Richtig sind also nur die <u>Aussagen 1 und 3</u>. | ||
| + | |||
| + | Die Bedingung für das zweite Nyquistkriterium lautet im Frequenzbereich: | ||
| + | :$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - | ||
| + | \frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= | ||
| + | {\rm const.}$$ | ||
| + | Die Bedingung ist beim cos$^{2}$–Spektrum tatsächlich erfüllt, wie man nach längerer Rechnung zeigen kann. Wir beschränken uns hier auf den Frequenzbereich $| f · T | \leq 1$ und setzen vereinfachend $g_{0} \cdot T = 1$: | ||
| + | :$$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} | ||
| + | - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) | ||
| + | \cdot T \right ]}+\frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} | ||
| + | + f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) | ||
| + | \cdot T \right ]}\hspace{0.05cm}.$$ | ||
| + | Weiter gilt: | ||
| + | :$$\frac {\cos^2 (x)}{\cos(2x)} = {1}/{2} \cdot \frac | ||
| + | {1+\cos(2x)}{\cos(2x)}= {1}/{2} \cdot \left [1+ \frac | ||
| + | {1}{\cos(2x)}\right ]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = {1}/{2} | ||
| + | \cdot \left [1+ \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} | ||
| + | - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} | ||
| + | + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$ | ||
| + | :$$\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos | ||
| + | \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm | ||
| + | \pi f T \right)$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = 2 - \frac {1}{\sin | ||
| + | (\pi f T)} + \frac {1}{\sin (\pi f T)} = 2 = {\rm const}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(5)''' Für $t = T/2$ liefert die angegebene Gleichung einen unbestimmten Wert (0 geteilt durch 0), der allerdings mit der Regel von l'Hospital ermittelt werden kann. Dazu bildet man die Ableitungen von Zähler und Nenner und setzt in das Ergebnis den gewünschten Zeitpunkt $t = T/2$ ein: | ||
| + | :$$\frac{g( t = T/2)}{g_0} = \ {{\rm si}(\pi \cdot \frac{t}{T}) | ||
| + | \cdot \frac{{\rm d}/{\rm d}t \left [ \cos(\pi \cdot | ||
| + | t/T)\right]}{{\rm d}/{\rm d}t\left [ 1 - (2 \cdot t/T)^2\right]}} | ||
| + | \bigg |_{t = T/2} = | ||
| + | = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{- \pi/T \cdot | ||
| + | \sin(\pi \cdot t/T)}{-2 \cdot (2 | ||
| + | \cdot t/T) \cdot (2/T)}} \bigg |_{t = T/2} = \frac {2}{\pi}\cdot | ||
| + | \frac {\pi}{4}\hspace{0.1cm}\underline { = 0.5}\hspace{0.05cm}.$$ | ||
| + | Ein zweiter Lösungsweg führt zu der Darstellung: | ||
| + | :$$\frac{g( t )}{g_0} = {\rm si}(\pi \cdot \frac{t}{T}) \cdot | ||
| + | \frac {\pi}{4} \cdot \big [ {\rm si}(\pi \cdot (t/T + 1/2)) + | ||
| + | {\rm si}(\pi \cdot (t/T - 1/2))\big] \hspace{0.05cm}.$$ | ||
| + | Der zweite Klammerausdruck kann wie folgt umgeformt werden: | ||
| + | :$$\frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} | ||
| + | \bigg ] = \ \frac {\pi}{4} \cdot \left [ \frac {{\rm sin}(\pi | ||
| + | \cdot t/T + \pi/2)}{\pi \cdot t/T + \pi/2} + \frac {{\rm sin}(\pi | ||
| + | \cdot t/T - \pi/2)}{\pi \cdot t/T - \pi/2}\right] = | ||
| + | \\ = \ \frac {1}{2} \cdot {\rm cos}(\pi | ||
| + | \cdot t/T )\cdot \left [ \frac {1}{2 \cdot t/T + 1} - \frac {1}{ 2 | ||
| + | \cdot t/T - 1}\right] = \\ | ||
| + | \\ = \ \frac {1}{2} \cdot {\rm cos}(\pi | ||
| + | \cdot t/T )\cdot \frac{1- 2 \cdot t/T + 1+ 2 \cdot t/T}{(1+ 2 | ||
| + | \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 | ||
| + | \cdot t/T)^2}\hspace{0.05cm}.$$ | ||
| + | Daraus folgt, dass beide Ausdrücke tatsächlich gleich sind. Für den Zeitpunkt $t = T/2$ gilt somit weiterhin: | ||
| + | :$$\frac{g( t = T/2)}{g_0} = {\rm si}( \frac{\pi}{2}) \cdot \frac | ||
| + | {\pi}{4} \cdot \left [ {\rm si}(\pi ) + {\rm si}(0)\right]= \frac | ||
| + | {2}{\pi}\cdot \frac {\pi}{4} = 0.5 \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 13:21, 5 November 2017
Betrachtet wird das Spektrum $G(f)$ mit cos$^{2}$–förmigem Verlauf entsprechend der Skizze. Dieses erfüllt das erste Nyquistkriterium:
- $$\sum_{k = -\infty}^{+\infty} G(f - \frac{k}{T} ) = {\rm const.}$$
Dementsprechend hat der zugehörige Impuls $g(t)$ Nulldurchgänge bei Vielfachen von $T$, wobei $T$ noch zu bestimmen ist. Durch Fourierrücktransformation von $G(f)$ erhält man die Gleichung für den Zeitverlauf:
- $$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\cdot {\rm si}(\pi \cdot {t}/{T})\hspace{0.05cm}.$$
In den Fragen zu dieser Aufgabe werden auf folgende Eigenschaften Bezug genommen:
- Die hier betrachtete Spektralfunktion $G(f)$ ist ein Sonderfall des Cosinus–Rolloff–Spektrums, das punktsymmetrisch um die Nyquistfrequenz $f_{\rm Nyq}$ ist.
- Das Cosinus–Rolloff–Spektrum ist durch die Eckfrequenzen $f_{1}$ und $f_{2}$ vollständig gekennzeichnet. Für $| f | < f_{1}$ ist $G(f) = g_{0} \cdot T = const.$, während das Spektrum für $| f | > f_{2}$ keine Anteile besitzt.
- Der Zusammenhang zwischen der Nyquistfrequenz und den Eckfrequenzen lautet:
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- Die Flankensteilheit wird durch den so genannten Rolloff–Faktor charakterisiert:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$
Hinweis:
Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Eigenschaften von Nyquistsystemen.
Fragebogen
Musterlösung
(2) Aus den angegebenen Gleichungen erhält man:
- $$f_{\rm Nyq} = \ \frac{f_1 +f_2 } {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},$$
- $$r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$
(3) Der Abstand äquidistanter Nulldurchgänge hängt direkt mit der Nyquistfrequenz zusammen:
- $$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm \mu s}}\hspace{0.05cm}.$$
(4) Die erste Aussage ist richtig: Die Funktion $si(π · t/T)$ führt zu Nulldurchgängen bei $\nu T (\nu \neq 0)$. Auch die letzte Aussage trifft zu: Wegen $g(t) = 0$ für $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ wird auch das zweite Nyquistkriterium erfüllt. Falsch ist dagegen die mittlere Aussage, da $g(t = T/2) \neq 0$ ist. Richtig sind also nur die Aussagen 1 und 3.
Die Bedingung für das zweite Nyquistkriterium lautet im Frequenzbereich:
- $$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - \frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$
Die Bedingung ist beim cos$^{2}$–Spektrum tatsächlich erfüllt, wie man nach längerer Rechnung zeigen kann. Wir beschränken uns hier auf den Frequenzbereich $| f · T | \leq 1$ und setzen vereinfachend $g_{0} \cdot T = 1$:
- $$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}+\frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\hspace{0.05cm}.$$
Weiter gilt:
- $$\frac {\cos^2 (x)}{\cos(2x)} = {1}/{2} \cdot \frac {1+\cos(2x)}{\cos(2x)}= {1}/{2} \cdot \left [1+ \frac {1}{\cos(2x)}\right ]$$
- $$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = {1}/{2} \cdot \left [1+ \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$
- $$\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm \pi f T \right)$$
- $$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = 2 - \frac {1}{\sin (\pi f T)} + \frac {1}{\sin (\pi f T)} = 2 = {\rm const}\hspace{0.05cm}.$$
(5) Für $t = T/2$ liefert die angegebene Gleichung einen unbestimmten Wert (0 geteilt durch 0), der allerdings mit der Regel von l'Hospital ermittelt werden kann. Dazu bildet man die Ableitungen von Zähler und Nenner und setzt in das Ergebnis den gewünschten Zeitpunkt $t = T/2$ ein:
- $$\frac{g( t = T/2)}{g_0} = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{{\rm d}/{\rm d}t \left [ \cos(\pi \cdot t/T)\right]}{{\rm d}/{\rm d}t\left [ 1 - (2 \cdot t/T)^2\right]}} \bigg |_{t = T/2} = = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{- \pi/T \cdot \sin(\pi \cdot t/T)}{-2 \cdot (2 \cdot t/T) \cdot (2/T)}} \bigg |_{t = T/2} = \frac {2}{\pi}\cdot \frac {\pi}{4}\hspace{0.1cm}\underline { = 0.5}\hspace{0.05cm}.$$
Ein zweiter Lösungsweg führt zu der Darstellung:
- $$\frac{g( t )}{g_0} = {\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac {\pi}{4} \cdot \big [ {\rm si}(\pi \cdot (t/T + 1/2)) + {\rm si}(\pi \cdot (t/T - 1/2))\big] \hspace{0.05cm}.$$
Der zweite Klammerausdruck kann wie folgt umgeformt werden:
- $$\frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {\pi}{4} \cdot \left [ \frac {{\rm sin}(\pi \cdot t/T + \pi/2)}{\pi \cdot t/T + \pi/2} + \frac {{\rm sin}(\pi \cdot t/T - \pi/2)}{\pi \cdot t/T - \pi/2}\right] = \\ = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \left [ \frac {1}{2 \cdot t/T + 1} - \frac {1}{ 2 \cdot t/T - 1}\right] = \\ \\ = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \frac{1- 2 \cdot t/T + 1+ 2 \cdot t/T}{(1+ 2 \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$
Daraus folgt, dass beide Ausdrücke tatsächlich gleich sind. Für den Zeitpunkt $t = T/2$ gilt somit weiterhin:
- $$\frac{g( t = T/2)}{g_0} = {\rm si}( \frac{\pi}{2}) \cdot \frac {\pi}{4} \cdot \left [ {\rm si}(\pi ) + {\rm si}(0)\right]= \frac {2}{\pi}\cdot \frac {\pi}{4} = 0.5 \hspace{0.05cm}.$$