Difference between revisions of "Aufgaben:Exercise 1.10Z: Gaussian Band-Pass"
| Line 4: | Line 4: | ||
[[File:P_ID1697__Dig_Z_4_3.png|right|frame|Gaußförmiger Bandpasskanal]] | [[File:P_ID1697__Dig_Z_4_3.png|right|frame|Gaußförmiger Bandpasskanal]] | ||
| − | + | Für diese Aufgabe setzen wir voraus: | |
| − | |||
| − | |||
| − | |||
*Zur Modulation wird binäre Phasenmodulation (BPSK) verwendet. | *Zur Modulation wird binäre Phasenmodulation (BPSK) verwendet. | ||
* Die Demodulation erfolgt frequenz– und phasensynchron. | * Die Demodulation erfolgt frequenz– und phasensynchron. | ||
| − | Zur Beschreibung benutzt man oft den äquivalenten TP–Frequenzgang $H_{\rm K,TP}(f)$. Dieser ergibt sich aus $H_{\rm K}(f)$ durch | + | Bei trägerfrequenzmodulierter Übertragung muss der Kanalfrequenzgang $H_{\rm K}(f)$ stets als Bandpass angesetzt werden. Die Kanalparameter sind zum Beispiel die Mittenfrequenz $f_{\rm M}$ und die Bandbreite $\Delta f_{\rm K}$, wobei die Mittenfrequenz $f_{\rm M}$ oft mit der Trägerfrequenz $f_{\rm T}$ übereinstimmt. |
| + | |||
| + | In dieser Aufgabe soll insbesondere von einem Gaußbandpass entsprechend der Grafik ausgegangen werden. Für dessen Frequenzgang gilt: | ||
| + | :$$H_{\rm K}(f) = {\rm exp} \left [ - \pi \cdot \left ( \frac {f - f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ] | ||
| + | +{\rm exp} \left [ - \pi \cdot \left ( \frac {f + f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ]$$ | ||
| + | |||
| + | Zur einfacheren Beschreibung benutzt man oft den äquivalenten TP–Frequenzgang $H_{\rm K,TP}(f)$. Dieser ergibt sich aus $H_{\rm K}(f)$ durch | ||
*Abschneiden der Anteile bei negativen Frequenzen, | *Abschneiden der Anteile bei negativen Frequenzen, | ||
*Verschieben des Spektrums um $f_{\rm T}$ nach links. | *Verschieben des Spektrums um $f_{\rm T}$ nach links. | ||
| − | |||
Im betrachteten Beispiel ergibt sich mit $f_{\rm T} = f_{\rm M}$ für den äquivalenten TP–Frequenzgang: | Im betrachteten Beispiel ergibt sich mit $f_{\rm T} = f_{\rm M}$ für den äquivalenten TP–Frequenzgang: | ||
| − | :$$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm | + | :$$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {f }/{\Delta f_{\rm K}}\right )^2 }.$$ |
Die entsprechende Zeitfunktion (Fouruerrücktransformierte) lautet: | Die entsprechende Zeitfunktion (Fouruerrücktransformierte) lautet: | ||
| − | :$$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm | + | :$$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {\Delta f_{\rm K}} \cdot t \right )^2 }.$$ |
Zur Beschreibung eines phasensynchronen BPSK–Systems im Tiefpassbereich eignet sich aber auch der Frequenzgang | Zur Beschreibung eines phasensynchronen BPSK–Systems im Tiefpassbereich eignet sich aber auch der Frequenzgang | ||
:$$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$ | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$ | ||
wobei „MKD” für Modulator – Kanal – Demodulator steht. Häufig – aber nicht immer – sind $H_{\rm MKD}(f)$ und $H_{\rm K,TP}(f)$ identisch. | wobei „MKD” für Modulator – Kanal – Demodulator steht. Häufig – aber nicht immer – sind $H_{\rm MKD}(f)$ und $H_{\rm K,TP}(f)$ identisch. | ||
| − | |||
| − | Die Aufgabe | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Lineare_digitale_Modulation_–_Kohärente_Demodulation|Lineare digitale Modulation – Kohärente Demodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Digitalsignalübertragung/Lineare_digitale_Modulation_–_Kohärente_Demodulation#Basisbandmodell_f.C3.BCr_ASK_und_BPSK|Basisbandmodell für ASK und BPSK]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Line 52: | Line 57: | ||
+Die Zeitfunktion $h_{\rm MKD}(t)$ ist reell. | +Die Zeitfunktion $h_{\rm MKD}(t)$ ist reell. | ||
| − | { | + | {Was sollte im Hinblick auf eine kleinere Bitfehlerwahrscheinlichkeit gelten? |
|type="[]"} | |type="[]"} | ||
| − | +$f_{\rm M} = f_{\rm T}$ | + | +$f_{\rm M} = f_{\rm T}$, |
- $f_{\rm M} \neq f_{\rm T}$. | - $f_{\rm M} \neq f_{\rm T}$. | ||
Revision as of 12:06, 8 November 2017
Für diese Aufgabe setzen wir voraus:
- Zur Modulation wird binäre Phasenmodulation (BPSK) verwendet.
- Die Demodulation erfolgt frequenz– und phasensynchron.
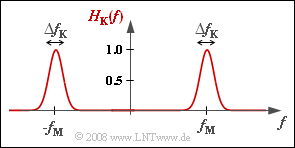
Bei trägerfrequenzmodulierter Übertragung muss der Kanalfrequenzgang $H_{\rm K}(f)$ stets als Bandpass angesetzt werden. Die Kanalparameter sind zum Beispiel die Mittenfrequenz $f_{\rm M}$ und die Bandbreite $\Delta f_{\rm K}$, wobei die Mittenfrequenz $f_{\rm M}$ oft mit der Trägerfrequenz $f_{\rm T}$ übereinstimmt.
In dieser Aufgabe soll insbesondere von einem Gaußbandpass entsprechend der Grafik ausgegangen werden. Für dessen Frequenzgang gilt:
- $$H_{\rm K}(f) = {\rm exp} \left [ - \pi \cdot \left ( \frac {f - f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ] +{\rm exp} \left [ - \pi \cdot \left ( \frac {f + f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ]$$
Zur einfacheren Beschreibung benutzt man oft den äquivalenten TP–Frequenzgang $H_{\rm K,TP}(f)$. Dieser ergibt sich aus $H_{\rm K}(f)$ durch
- Abschneiden der Anteile bei negativen Frequenzen,
- Verschieben des Spektrums um $f_{\rm T}$ nach links.
Im betrachteten Beispiel ergibt sich mit $f_{\rm T} = f_{\rm M}$ für den äquivalenten TP–Frequenzgang:
- $$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {f }/{\Delta f_{\rm K}}\right )^2 }.$$
Die entsprechende Zeitfunktion (Fouruerrücktransformierte) lautet:
- $$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {\Delta f_{\rm K}} \cdot t \right )^2 }.$$
Zur Beschreibung eines phasensynchronen BPSK–Systems im Tiefpassbereich eignet sich aber auch der Frequenzgang
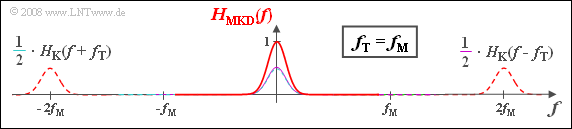
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$
wobei „MKD” für Modulator – Kanal – Demodulator steht. Häufig – aber nicht immer – sind $H_{\rm MKD}(f)$ und $H_{\rm K,TP}(f)$ identisch.
Hinweise:
- Die Aufgabe gehört zum Kapitel Lineare digitale Modulation – Kohärente Demodulation.
- Bezug genommen wird insbesondere auf die Seite Basisbandmodell für ASK und BPSK.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$H_{\rm K}(f) = H_{\rm K,\hspace{0.04cm} TP}(f) \star \left [ \delta (f - f_{\rm M}) + \delta (f + f_{\rm M}) \right ] .$$
Die Fourierrücktransformierte des Klammerausdrucks liefert eine Cosinusfunktion der Frequenz $f_{\rm M}$ mit der Amplitude 2. Nach dem Faltungssatz gilt somit:
- $$h_{\rm K}(t) = 2 \cdot \Delta f_{\rm K} \cdot {\rm exp} \left [ - \pi \cdot \left ( {\Delta f_{\rm K}} \cdot t \right )^2 \right ] \cdot \cos(2 \pi f_{\rm M} t ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm K}(t = 0)/\Delta f_{\rm K} \hspace{0.1cm}\underline {= 2}.$$
Das heißt: Die TP–Impulsantwort $h_{\rm K,TP}(t)$ ist formgleich mit der Hüllkurve der BP–Impulsantwort $h_{\rm K}(t)$, aber doppelt so groß.
(2) Die erste Aussage ist falsch, da $H_{\rm MKD}(f)$ auch Anteile um $\pm 2f_{\rm T}$ besitzt. Die Zeitfunktion $h_{\rm K,TP}(t)$ ist entsprechend der angegebenen Gleichung reell. Gleiches gilt für $h_{\rm MKD}(t)$ auch unter Berücksichtigung der $\pm 2f_{\rm T}$–Anteile, da $H_{\rm MKD}(f)$ eine bezüglich $f = 0$ gerade Funktion ist. Richtig sind also die Aussagen 2, 3 und 4. Die Grafik zeigt den Frequenzgang $H_{\rm MKD}(f)$, der auch Anteile um $\pm 2f_{\rm T}$ besitzt. Bei tiefen Frequenzen ist $H_{\rm K,TP}(f)$ identisch mit $H_{\rm MKD}(f)$.
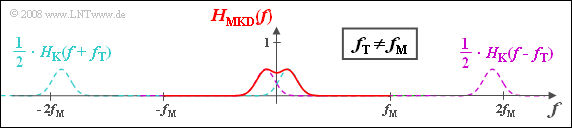
(3) Hier unterscheiden sich $H_{\rm K,TP}(f)$ und $H_{\rm MKD}(f)$ auch bei den tiefen Frequenzen. $H_{\rm K,TP}(f)$ ist eine Gaußfunktion mit dem Maximum bei $f_{ε} = f_{\rm M} – f_{\rm T}$. Aufgrund dieser Unsymmetrie ist $h_{\rm K,TP}(t)$ komplex. Dagegen ist $H_{\rm MKD}(f)$ weiterhin eine bezüglich $f = 0$ gerade Funktion mit reeller Impulsantwort $h_{\rm MKD}(t)$. $H_{\rm MKD}(f)$ setzt sich aus zwei Gaußfunktionen bei $± f_ε$ zusammen. Richtig ist nur der Lösungsvorschlag 4.
(4) Richtig ist natürlich die erste Antwort.