Aufgaben:Exercise 2.1: ACF and PSD with Coding

• Return to book

Leistungsdichtespektrum bei Codierung

Wir betrachten das Digitalsignal $s(t)$, wobei wir folgende Beschreibungsgrößen verwenden:

• $a_{\nu}$ sind die Amplitudenkoeffizienten,
• $g_{s}(t)$ gibt den Sendegrundimpuls an,
• $T$ ist die Symboldauer (Abstand der Impulse).

Dann gilt:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$

Zur Charakterisierung der spektralen Eigenschaften, die sich aufgrund der Codierung und der Impulsformung ergeben, verwendet man unter anderem

• die Autokorrelationsfunktion (AKF)

$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm},$$

• das Leistungsdichtespektrum (LDS)

$${\it \Phi}_s(f) = {1}/{T} \cdot {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \hspace{0.05cm}.$$

Hierbei bezeichnet $\varphi_{a}(\lambda)$ die diskrete Autokorrelationsfunktion der Amplitudenkoeffizienten, die mit der spektralen Leistungsdichte ${\it \Phi}_{a}(f)$ über die Fouriertransformation zusammenhängt. Für diese gilt somit:

$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$

Weiterhin sind in obigen Gleichungen die Energie–AKF und das Energiespektrum verwendet:

$$\varphi^{^{\bullet}}_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm}.$$

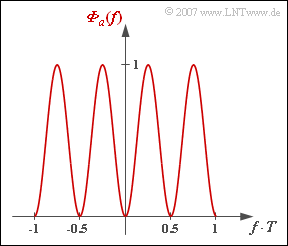
In der vorliegenden Aufgabe soll für die spektrale Leistungsdichte der Amplitudenkoeffizienten folgender Funktionsverlauf angenommen werden (siehe Grafik):

$${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$

Für den Sendegrundimpuls werden folgende Annahmen getroffen:

• In der Teilfrage (2) sei $g_{s}(t)$ ein NRZ–Rechteckimpuls, so dass eine dreieckförmige Energie–AKF vorliegt, die auf den Bereich $|\tau| ≤ T$ beschränkt ist. Das Maximum ist dabei

$$\varphi^{^{\bullet}}_{gs}(\tau = 0) = s_0^2 \cdot T \hspace{0.05cm}.$$

• Für die Teilaufgabe (3) soll von einer Wurzel–Nyquist–Charakteristik mit Rolloff–Faktor $r = 0$ ausgegangen werden. In diesem Fall gilt:

$$|G_s(f)|^2 = \left\{ \begin{array}{c} s_0^2 \cdot T^2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} |f| < {1}/({2T}) \hspace{0.05cm}, \\ |f| > {1}/({2T}) \hspace{0.05cm}.\\ \end{array}$$

• Für numerische Berechnungen ist stets $s_{0}^{2} = 10 \ \rm mW$ zu verwenden.

Hinweise:

• Die Aufgabe gehört zum Kapitel Grundlagen der codierten Übertragung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Berücksichtigen Sie, dass die Sendeleistung $P_{\rm S}$ gleich der AKF $\varphi_{s}(\tau)$ an der Stelle $\tau = 0$ ist, aber auch als Integral über das LDS $\Phi_{s}(f)$ berechnet werden kann.

Fragebogen

1

Welche diskreten AKF–Werte $\varphi_{a}(\lambda)$ der Amplitudenkoeffizienten ergeben sich? Geben Sie die Zahlenwerte für $\lambda = 0$, $\lambda = 1$ und $\lambda = 2$ ein.

$\varphi_{a}(\lambda = 0) \ = \ $

$\varphi_{a}(\lambda = 1) \ = \ $

$\varphi_{a}(\lambda = 2) \ = \ $

2

Welche Sendeleistung ergibt sich mit dem NRZ–Sendegrundimpuls?

$P_{\rm S} \ = \ $ $ \ \rm mW$

3

Wie groß ist die Sendeleistung bei Wurzel–Nyquist–Charakteristik $(r = 0)$?

$P_{\rm S} \ = \ $ $ \ \rm mW$

Musterlösung

Solution

(1)  Da $\Phi_{a}(f)$ als eine spektrale Leistungsdichte stets reell ist (dazu gerade und positiv, aber das spielt hier keine Rolle) und die AKF–Werte $\varphi_{a}(\lambda)$ symmetrisch um $\lambda = 0$ sind, kann die angegebene Gleichung wie folgt umgewandelt werden:

$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(0) + \sum_{\lambda = 1}^{\infty}2 \cdot \varphi_a(\lambda)\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) \hspace{0.05cm}.$$

Durch Vergleich mit der skizzierten Funktion

$${\it \Phi}_a(f) = {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\hspace{0.05cm}.$$

erhält man:

$${\it \varphi}_a(\lambda = 0)\hspace{0.15cm}\underline { = 0.5}, \hspace{0.2cm} {\it \varphi}_a(\lambda = 2) = {\it \varphi}_a(\lambda = -2) \hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm}.$$

Alle anderen AKF–Werte – also auch $\varphi_{a}(\lambda = ±1)$ – ergeben sich zu $0$.

(2)  Für den rechteckförmigen NRZ–Grundimpuls ergibt sich aufgrund der Begrenzung der Energie–AKF auf den Bereich $|\tau| ≤ T$:

$$P_{\rm S} = \varphi_s(\tau = 0) = \frac{1}{T} \cdot \varphi_a(\lambda = 0)\cdot \varphi^{^{\bullet}}_{gs}(\tau = 0)= \frac{1}{T} \cdot \frac{1}{2} \cdot s_0^2 \cdot T = \frac{s_0^2}{2} \hspace{0.15cm}\underline {= 5\,\,{\rm mW}}\hspace{0.05cm}.$$

(3)  Im hier zu betrachtenden Fall (rechteckförmige Spektralfunktion) ist es günstiger, die Sendeleistung durch Integration über das Leistungsdichtespektrum zu berechnen:

$$P_{\rm S} = \ \int_{-1/(2T)}^{+1/(2T)} {\it \Phi}_s(f) \,{\rm d} f = \frac{1}{T} \cdot \int_{-1/(2T)}^{+1/(2T)} {\it \Phi}_a(f) \cdot {\it \Phi}^{^{\bullet}}_{gs}(f) \,{\rm d} f =$$

$$\hspace{0.6cm}= \ \frac{1}{T} \cdot \left [ s_0^2 \cdot T^2 \right ] \cdot \int_{-1/(2T)}^{+1/(2T)} \left( {1}/{2} - {1}/{2} \cdot \cos (4 \pi f \hspace{0.02cm} T)\right ) \,{\rm d} f\hspace{0.05cm} = {s_0^2}/{2}\hspace{0.15cm}\underline { = 5\,\,{\rm mW}} .$$

Hierbei ist berücksichtigt, dass für diese Aufgabe das Energie–LDS $|G_{s}(f)|^{2}$ als konstant vorgegeben ist (innerhalb des Integrationsintervalls) und somit vor das Integral gezogen werden kann. Trotz völlig anderer Signalform $s(t)$ ergibt sich hier die gleiche Sendeleistung, da das Integral den Wert $1/(2T)$ liefert. Anzumerken ist, dass diese einfache Rechnung nur für den Rolloff-Faktor $r = 0$ möglich ist.