Aufgaben:Exercise 2.3: Binary Signal and Quaternary Signal

• Return to book

AKF und LDS von Binärsignal und Quaternärsignal

Es sollen zwei redundanzfreie Übertragungssysteme B und Q jeweils mit bipolaren Amplitudenkoeffizienten $a_{\nu}$ vergleichend gegenübergestellt werden. Beide Systeme erfüllen die erste Nyquistbedingung. Gemäß der Wurzel–Wurzel–Aufteilung ist das Spektrum $G_{d}(f)$ des Detektionsgrundimpulses formgleich mit der spektralen Leistungsdichte $\Phi_{s}(f)$ des Sendesignals. Bekannt sind folgende Eigenschaften der beiden Systeme:

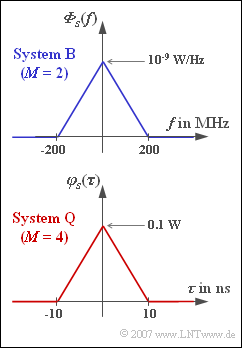
• Vom binären System B ist die spektrale Leistungsdichte $\Phi_{s}(f)$ am Sender bekannt und in der Grafik zusammen mit den Beschreibungsparametern dargestellt.
• Das System Q benutzt ein NRZ–Rechtecksignal mit den vier möglichen Amplitudenwerten $±s_{0}$ und $±s_{0}/3$, die alle mit gleicher Wahrscheinlichkeit auftreten.
• ${s_{0}}^{2}$ hat die Einheit einer Leistung und gibt die maximale Momentanleistung an, die nur dann auftritt, wenn eines der beiden „äußeren Symbole” gesendet wird.
• Die Beschreibungsparameter von System Q können der dreieckförmigen AKF in nebenstehender Grafik entnommen werden.

Hinweis:

Die Aufgabe bezieht sich auf Grundlagen der codierten Übertragung und Redundanzfreie Codierung dieses Buches. Berücksichtigen Sie bei der Lösung, dass bei einem stochastischen Signal die Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) stets über die Fouriertransformation zusammenhängen.

Fragebogen

1

Welche Symboldauer $T$ hat das Binärsystem mit Nyquisteigenschaft?

System ${\rm B}: T \ = \ $ $\ \rm ns$

2

Wie groß ist die (äquivalente) Bitrate des Binärsystems?

System ${\rm B}: R_{\rm B} \ = \ $ $\ \rm Mbit/s$

3

Welche Leistung besitzt das binäre Sendesignal?

System ${\rm B}: P_{\rm S} \ = \ $ $\ \rm mW$

4

Welche Aussagen sind bezüglich des Binärsystems zutreffend?

	Die AKF $\varphi_{s}(\tau)$ des Sendesignals ist $\rm si^{2}$–förmig.
	Die Energie–AKF $\varphi^{^{\bullet}}_{gs}(\tau)$ des Grundimpulses ist $\rm si^{2}$–förmig.
	Der Sendegrundimpuls $g_{s}(t)$ selbst ist $\rm si^{2}$–förmig.

5

Welche Symboldauer weist das Quaternärsystem auf?

System ${\rm Q}: T \ = \ $ $\ \rm ns$

6

Wie groß ist die äquivalente Bitrate des Quaternärsignals?

System ${\rm Q}: R_{\rm B} \ = \ $ $\ \rm Mbit/s$

7

Welche Leistung besitzt das quaternäre Sendesignal?

System ${\rm Q}: P_{\rm S} \ = \ $ $\ \rm mW$

8

Welche maximale momentane Sendeleistung besitzt das Quaternärsignal?

System ${\rm Q}: {s_{0}}^{2} \ = \ $ $\ \rm mW$

Musterlösung

Solution

(1)  Die Nyquistfrequenz $f_{\rm Nyq} = 100 \ \rm MHz$ kann aus der Grafik abgelesen werden. Daraus folgt mit den Aussagen von Eigenschaften von Nyquistsystemen :

$$f_{\rm Nyq} = \frac{1 } {2 \cdot T} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T = \frac{1 } {2 \cdot f_{\rm Nyq}} \hspace{0.15cm}\underline{ =5\,{\rm ns}}\hspace{0.05cm}.$$

(2)  Beim Binärsystem ist die Bitrate gleichzeitig der Informationsfluss und es gilt:

$$R_{\rm B} = {1 }/ { T} \hspace{0.15cm}\underline {= 200\,{\rm Mbit/s}}= 2 \cdot f_{\rm Nyq} \cdot{\rm bit}/{\rm Hz}\hspace{0.05cm}.$$

(3)  Die Sendeleistung ist gleich dem Integral über $\it \Phi_{s}(f)$ und kann als Dreiecksfläche berechnet werden:

$$P_{\rm S} = \ \int_{-\infty}^{+\infty} {\it \Phi}_s(f) \,{\rm d} f = 10^{-9} \frac{\rm W}{\rm Hz} \cdot 200\,\,{\rm MHz} \hspace{0.15cm}\underline { = 200\,\,{\rm mW}}.$$

(4)  Richtig sind die beiden ersten Aussagen. Die Fourierrücktransformierte des Leistungsdichtespektrums $\it \Phi_{s}(f)$ ergibt die $\rm si^{2}$–förmige AKF $\varphi_{s}(\tau)$. Allgemein gilt zudem folgender Zusammenhang:

$$ \varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$

Bei einem redundanzfreien Binärsystem gilt jedoch $\varphi_{a}(\lambda = 0) = 1$, während alle anderen diskreten AKF–Werte $\varphi_{a}(\lambda \neq 0)$ gleich $0$ sind. Somit hat auch die Energie–AKF einen $\rm si^{2}$–förmigen Verlauf:

$$\varphi^{^{\bullet}}_{gs}(\tau ) = T \cdot \varphi_s(\tau) \hspace{0.05cm}.$$

Hinweis: Energie–AKF und Energie–LDS werden in diesem Tutorial jeweils mit Punkt versehen.

Dagegen trifft die letzte Aussage nicht zu. Für die folgende Begründung nehmen wir vereinfachend an, dass $g_{s}(t)$ symmetrisch sei und somit $G_{s}(f)$ reell ist. Dann gilt:

$${\it \Phi}_{s}(f) = {1 }/ { T} \cdot |G_s(f)|^2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_s(f) = \sqrt{{ T} \cdot {\it \Phi}_{s}(f)}\hspace{0.4cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm}g_s(t) \hspace{0.05cm}.$$

Aufgrund der Quadratwurzel in der obigen Gleichung ist der Sendegrundimpuls $g_{s}(t)$ nicht $\rm si^{2}$–förmig im Gegensatz zum Detektionsgrundimpuls $g_{d}(t)$, der formgleich mit der Energie–AKF $\varphi^{^{\bullet}}_{gs}(\tau)$ und damit $\rm si^{2}$–förmig ist. Gleichzeitig gilt $\varphi^{^{\bullet}}_{gs}(\tau) = g_{s}(\tau) ∗ g_{s}(–\tau)$.

(5)  Die AKF $\varphi_{s}(\tau)$ ist auf den Bereich $|\tau| ≤ T$ begrenzt, wenn der Sendegrundimpuls ein NRZ–Rechteck ist. Somit ergibt sich aus der Grafik die Symboldauer $T \underline{= 10 \ \rm ns}$.

(6)  Beim Quaternärsignal ergibt sich wegen der doppelten Symboldauer der gleiche Informationsfluss wie beim obigen Binärsignal:

$$R_{\rm B} = {{\rm log_2(4)} }/ { T} \hspace{0.15cm}\underline {= 200\,\,{\rm Mbit/s}}\hspace{0.05cm}.$$

(7)  Die Sendeleistung ist gleich dem AKF–Wert bei $\tau = 0$ und kann aus der Grafik abgelesen werden:

$$P_{\rm S} = \hspace{0.15cm}\underline {100\,\,{\rm mW}}.$$

(8)  Beim redundanzfreien Quaternärsignal mit NRZ–Rechteckimpulsen gilt für die mittlere Sendeleistung:

$$P_{\rm S} = {1}/ { 4} \cdot \left [ (-s_0)^2 + (-s_0/3)^2 + (+s_0/3)^2 +(+s_0)^2 \right ] = {5}/ { 9} \cdot s_0^2$$

$$\Rightarrow \hspace{0.3cm}s_0^2 = {9}/ {5} \cdot P_{\rm S} = {9}/ {5} \cdot 100\,\,{\rm mW}\hspace{0.15cm}\underline { = 180\,\,{\rm mW}}\hspace{0.05cm}.$$