Aufgaben:Exercise 4.19: Orthogonal Multilevel FSK

• Return to book

Vorgegebene Signalraumkonstellationen

Wir betrachten in dieser letzten Übungsaufgabe zu diesem Kapitel Frequency Shift Keying (FSK) mit $M$ Signalformen und setzen voraus, dass diese paarweise zueinander orthogonal sind. In diesem Fall können die äquivalenten Tiefpass–Signale $s_i(t)$ mit $i = 1, \ ... \ , M$ in folgender Form dargestellt werden:

$$s_i(t) = \sqrt{E_{\rm S}} \cdot \xi_i(t) \hspace{0.05cm}.$$

$\xi_i(t)$ sind komplexe Basisfunktionen, für die allgemein $i = 1, \ ... \ , N$ gilt. Bei orthogonaler Signalisierung ist allerdings stets $M = N$.

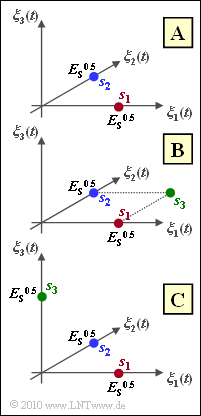
Die Grafik zeigt drei verschiedene Signalraumkonstellationen. Jedoch beschreiben nicht alle drei eine orthogonale FSK. Hierauf wird in der Teilaufgabe (1) Bezug genommen.

Im Theorieteil ist die exakte Formel für die Wahrscheinlichkeit einer korrekten Entscheidung bei AWGN–Störung angegeben:

$${\rm Pr}({\cal{C}}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot $$

$$\hspace{-0.1cm} \ \cdot \ \hspace{-0.1cm} {\rm exp } \left [ - \frac{i } {(i+1) }\cdot \frac{ E_{\rm S} } { N_0}\right ] \hspace{0.05cm}.$$

Daraus lässt sich sehr einfach die Symbolfehlerwahrscheinlichkeit berechnen:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = 1 - {\rm Pr}({\cal{C}}) = \sum_{i = 1}^{M-1} (-1)^{i+1} \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm exp } \left [ - \frac{i } {(i+1) }\cdot \frac{ E_{\rm S} } { N_0}\right ] \hspace{0.05cm}.$$

Eine obere Schranke ($p_{\rm S, \ max} ≥ p_{\rm S}$) ergibt sich aufgrund der alternierenden Vorzeichen, wenn man von dieser Summe nur den ersten Term berücksichtigt:

$$p_{\rm S, \hspace{-0.05cm}max} = \frac {M-1}{ 2} \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})} \hspace{0.05cm}.$$

In der Teilaufgabe (4) soll diese Schranke bei gegebenem Verhältnis $E_{\rm B}/N_0$ ausgewertet werden, wobei $E_{\rm B}$ die mittlere Signalenergie pro Bit angibt:

$$E_{\rm B} = \frac{ E_{\rm S} } { {\rm log_2}\hspace{0.1cm}(M)} \hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe bezieht sich auf die letzte Theorieseite des Kapitels Trägerfrequenzsysteme mit nichtkohärenter Demodulation.

Fragebogen

1

Welche der obigen Signalraumkonstellationen gelten für orthogonale FSK?

	Konstellation A,
	Konstellation B,
	Konstellation C.

2

Berechnen Sie für $E_{\rm S}/N_0 = 6$ die Fehlerwahrscheinlichkeit der binären, ternären und quaternären FSK. $E_{\rm S}$ bezeichnet die Symbolenergie.

$M = 2 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $

$M = 3 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $

$M = 4 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $

3

Berechnen Sie für $E_{\rm S}/N_0 = 6$ die Fehlerwahrscheinlichkeit der binären, ternären und quaternären FSK. $E_{\rm S}$ bezeichnet die Symbolenergie.

$E_{\rm S}/N_0 = 6, M = 2 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $

$\hspace{2.3cm} M = 3 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $

$\hspace{2.3cm} M = 4 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)