Aufgaben:Exercise 5.1: Error Distance Distribution

• Return to book

Gegebene Fehlerabstandsverteilung

Ein jedes digitales Kanalmodell kann in gleicher Weise beschrieben werden durch

• die Fehlerfolge $〈e_{\rm \nu}〉$,
• durch die Fehlerabstandsfolge $〈a_{\rm \nu '}〉$.

Beispielhaft betrachten wir die Folgen:

$$<\hspace{-0.1cm}e_{\nu} \hspace{-0.1cm}> \ = \ < \hspace{-0.1cm}0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, ... \hspace{-0.1cm}> \hspace{0.05cm},$$

$$< \hspace{-0.1cm}a_{\nu\hspace{0.05cm} '} \hspace{-0.15cm}> \ = \ <\hspace{-0.1cm}2, 3, 1, 4, 2, 5, 1, 1, 3, 4, 1, 2, ... \hspace{-0.1cm}> \hspace{0.05cm}.$$

Man erkennt daraus beispielsweise:

• Der Fehlerabstand $a_2 = 3$ bedeutet, dass zwischen dem ersten und dem zweiten Fehler zwei fehlerfreie Symbole liegen.
• $a_3 = 1$ deutet dagegen darauf hin, dass nach dem zweiten direkt ein dritter Fehler folgt.

Die unterschiedlichen Laufindizes ($\nu$ und $\nu '$, jeweils beginnend mit $1$) sind erforderlich, da keine Synchronität zwischen der Fehlerabstandsfolge und der Fehlerfolge besteht.

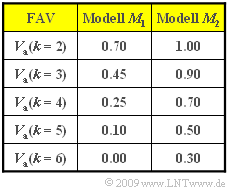
In der Grafik ist für zwei verschiedene Modelle $M_1$ und $M_2$ die Fehlerabstandsverteilung (FAV)

$$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}$$

angegeben. Diese Tabelle soll in dieser Aufgabe ausgewertet werden.

Hinweis: Die Aufgabe gehört zum Themengebiet des Kapitels Beschreibungsgrößen digitaler Kanalmodelle.

Fragebogen

1

Wie lauten die folgenden Fehlerwerte (0 oder 1)?

$e_{\rm 16} \ = \ $

$e_{\rm 17} \ = \ $

$e_{\rm 18} \ = \ $

2

Wie groß ist bei beiden Modellen $V_a(k = 1)$?

$V_a(k = 1) \ = \ $

3

Bestimmen Sie für das Modell $M_1$ die Wahrscheinlichkeiten der Fehlerabstände.

$M_1 \text {:} \hspace{0.2cm} {\rm Pr}(a = 1) \ = \ $

$M_1 \text {:} \hspace{0.2cm} {\rm Pr}(a = 2) \ = \ $

$M_1 \text {:} \hspace{0.2cm} {\rm Pr}(a = 3) \ = \ $

$M_1 \text {:} \hspace{0.2cm} {\rm Pr}(a = 4) \ = \ $

$M_1 \text {:} \hspace{0.2cm} {\rm Pr}(a = 5) \ = \ $

4

Multiple-Choice

	correct
	false

5

Input-Box Frage

$xyz$ = $ab$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)