Aufgaben:Exercise 2.7: AMI Code

• Return to book

Blockschaltbild eines Pseudoternärcoders

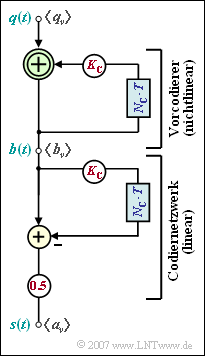
Die Grafik zeigt das Blockschaltbild zur AMI–Codierung, wobei von den binären bipolaren Amplitudenkoeffizienten $q_{\nu} ∈ \{–1, +1\}$ am Eingang ausgegangen wird. Diese Umcodierung erfolgt zweistufig:

• Im ersten Teil des Blockschaltbildes wird bei jedem Taktschritt ein binär–vorcodiertes Symbol $b_{\nu}$ aus der Modulo–2–Addition von $q_{\nu}$ und $b_{\nu -1}$ erzeugt. Es gilt $b_{\nu} ∈ \{–1, +1\}.$
• Danach wird durch eine herkömmliche Subtraktion der aktuelle Amplitudenkoeffizient des ternären Sendesignals $s(t)$ bestimmt. Dabei gilt:

$$a_\nu = {1}/{2} \cdot \left [ b_\nu - b_{\nu-1} \right ] \hspace{0.05cm}.$$

Aufgrund der AMI–Codierung wird sichergestellt, dass keine langen „$+1$”– bzw. „$–1$”–Sequenzen entstehen. Um auch lange Nullfolgen zu vermeiden, wurden auch modifizierte AMI–Codes entwickelt:

• Beim HDB3–Code werden je vier aufeinanderfolgende Nullen durch eine gezielte Verletzung der AMI–Codierregel markiert.
• Beim B6ZS–Code werden sechs aufeinanderfolgende Nullen durch eine gezielte Verletzung der AMI–Codierregel markiert.

Das Leistungsdichtespektrum ${\it \Phi}_{a}(f)$ der Amplitudenkoeffizienten soll aus den diskreten AKF–Werten $\varphi_{a}(\lambda) = {\E}[a_{\nu} \cdot a_{\nu + \lambda}]$ ermittelt werden. Die Fouriertransformation lautet in dieser diskreten Darstellung:

$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$

Hinweis:

Die Aufgabe bezieht sich auf Symbolweise Codierung mit Pseudoternärcodes. Sie können Ihre Ergebnisse mit folgendem Interaktionsmodul überprüfen: Signale, AKF und LDS der Pseutoternärcodes

Fragebogen

1

Am Eingang liegt $\langle q_{\nu} \rangle = \langle +1, –1, +1, +1, –1, +1, +1, –1, –1, –1, –1, +1 \rangle$ an. Ermitteln Sie die binär–vorcodierte Folge $\langle b_{\nu} \rangle$ mit der Vorbelegung $b_{0} = –1$. Geben Sie zur Kontrolle folgende Werte ein:

$b_{1} \ = \ $

$b_{11} \ = \ $

$b_{12} \ = \ $

2

Ermitteln Sie die Folge $\langle a_{\nu} \rangle$ der Amplitudenkoeffizienten des AMI–codierten Sendesignals $s(t)$. Geben Sie zur Ergebnisüberprüfung folgende Werte ein:

$a_{1} \ = \ $

$a_{11} \ = \ $

$a_{12} \ = \ $

3

Würde sich ein HDB3– bzw. ein B6ZS–Signal im betrachteten Bereich $(12T)$ vom AMI–Code unterscheiden?

	Der HDB3–Code unterscheidet sich vom AMI–Code.
	Der B6ZS–Code unterscheidet sich vom AMI–Code.

4

Wie groß sind die drei Auftrittswahrscheinlichkeiten beim AMI–Code?

${\Pr}(a_{\nu} = + 1) \ = \ $

${\Pr}(a_{\nu} = 0) \ = \ $

${\Pr}(a_{\nu} = - 1) \ = \ $

5

Berechnen Sie die beiden ersten Mittelwerte der Amplitudenkoeffizienten.

$\E[a_{\nu}] \ = \ $

$\E[a_{\nu}^{2}] \ = \ $

6

Berechnen Sie die diskrete AKF $\varphi_{a}(\lambda)$, insbesondere die AKF–Werte

$\varphi_{a}(\lambda = 0) \ = \ $

$\varphi_{a}(\lambda = 1) \ = \ $

$\varphi_{a}(\lambda = 0) \ = \ $

7

Wie lautet das LDS ${\it \Phi}_{a}(f)$?. Welche Werte ergeben für $f = 0$ und $f = 1/(2T)$?

${\it \Phi}_{a}(f = 0) \ = \ $

${\it \Phi}_{a}(f = 1/(2T)) \ = \ $

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)