Aufgaben:Exercise 5.6Z: Gilbert-Elliott Model

• Return to book

GE–Modell

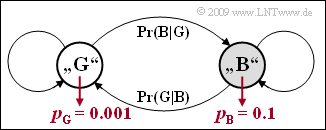
Wir betrachten das Bündelfehler–Kanalmodell nach E.N. Gilbert und E.O. Elliott (siehe Skizze). Für die Übergangswahrscheinlichkeiten soll dabei gelten:

$${\rm Pr}(\rm

G\hspace{0.05cm}|\hspace{0.05cm} B)= 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$

Die Fehlerwahrscheinlichkeit im Zustand „GOOD” betrage $p_{\rm G} = 0.1\%$ und für die im Zustand „BAD” gelte $p_{\rm B} = 10\%$. Im Verlaufe dieser Aufgabe sollen weitere Kenngrößen ermittelt werden:

• die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$,
• die Zustandswahrscheinlichkeiten $w_{\rm G} = \rm Pr(Z = G)$ und $w_{\rm B} = \rm Pr(Z = B)$,
• die Werte der Korrelationsfunktion, die für $k > 0$ analytisch wie folgt gegeben ist:

$$\varphi_{e}(k) = p_{\rm M}^2 + (p_{\rm B} -

p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot

[1 - {\rm Pr}(\rm

B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} \hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe bezieht sich auf das Kapitel Bündelfehlerkanal des vorliegenden Buches sowie auf das Kapitel Markovketten im Buch „Stochastische Signaltheorie”.

Fragebogen

1 Wie lauten die folgenden Übergangswahrscheinlichkeiten?

$\rm Pr(G|G) \ = \ $

$\rm Pr(B|B) \ = \ $

2 Mit welchen Wahrscheinlichkeiten befindet sich das GE–Modell im Zustand „GOOD” ($w_{\rm G}$) bzw. im Zustand „BAD” ($w_{\rm B}$)?

$\rm Pr(G|G) \ = \ $

3 Berechnen Sie die folgenden FKF–Werte:

$\varphi_e(k = 1) \ = \ $ $\ \cdot 10^{–4}$

$\varphi_e(k = 2) \ = \ $ $\ \cdot 10^{–4}$

$\varphi_e(k = 5) \ = \ $ $\ \cdot 10^{–4}$

$\varphi_e(k = 50) \ = \ $ $\ \cdot 10^{–4}$

4 Wie groß ist der FKF–Wert $\varphi_e(k = 0)$?

$\varphi_e(k = 0) \ = \ $ $\ \cdot 10^{–2}$

5 Lässt sich die mittlere Fehlerwahrscheinlichkeit $p_{\rm M} = 0.005$ erreichen durch

	alleinige Änderung von $p_{\rm G}$,
	alleinige Änderung von $p_{\rm B}$,
	alleinige Änderung von $\rm Pr(G|B)$,
	alleinige Änderung von $\rm Pr(B|G)$?

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)