Difference between revisions of "Aufgaben:Exercise 4.1: Log Likelihood Ratio"
From LNTwww
(Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Fr…“) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder | + | {{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder}} |
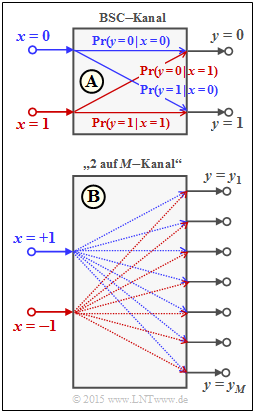
| + | [[File:P_ID2979__KC_A_4_1_v2.png|right|frame|Betrachtete Kanalmodelle]] | ||
| + | Zur Interpretation von <i>Log–Likelihood–Verhältnissen</i> (kurz $L$–Werten) gehen wir wie im [[Theorieteil]] vom <i>Binary Symmetric Channel</i> (BSC) aus. Die englische Bezeichung ist <i>Log Likelihood Ratio</i> (LLR). | ||
| + | Für die binären Zufallsgrößen am Eingang und Ausgang gelte | ||
| + | :$$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} | ||
| + | \hspace{0.05cm}. $$ | ||
| + | Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als [[Modell A]] bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt: | ||
| + | ::<math>{\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} & = & \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},\\ | ||
| + | {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} & = & \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $xyz \ = \ ${ 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
| − | '''2 | + | '''(2)''' |
| − | '''3 | + | '''(3)''' |
| − | '''4 | + | '''(4)''' |
| − | '''5 | + | '''(5)''' |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | + | [[Category:Aufgaben zu Kanalcodierung|^4.1 Soft–in Soft–out Decoder^]] | |
| − | [[Category:Aufgaben zu Kanalcodierung|^4.1 Soft–in Soft–out Decoder | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ^]] | ||
Revision as of 09:12, 6 December 2017
Zur Interpretation von Log–Likelihood–Verhältnissen (kurz $L$–Werten) gehen wir wie im Theorieteil vom Binary Symmetric Channel (BSC) aus. Die englische Bezeichung ist Log Likelihood Ratio (LLR).
Für die binären Zufallsgrößen am Eingang und Ausgang gelte
- $$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}. $$
Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als Modell A bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt:
- \[{\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} & = & \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},\\ {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} & = & \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.\]
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)