Difference between revisions of "Aufgaben:Exercise 2.6: Modified MS43 Code"
| Line 5: | Line 5: | ||
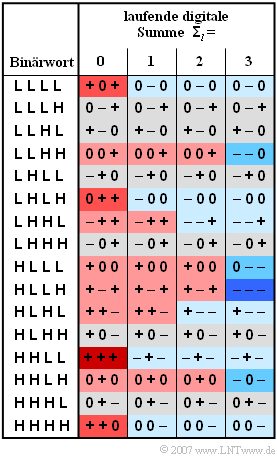
[[File:P_ID1340__Dig_A_2_6.png|right|frame|Codetabelle des MMS43-Codes]] | [[File:P_ID1340__Dig_A_2_6.png|right|frame|Codetabelle des MMS43-Codes]] | ||
| − | Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $\rm {U_{ | + | Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $\rm {U_{K0}}$–Schnittstelle, die den Übertragungsweg zwischen Vermittlungsstelle und Wohnung beschreibt, der MMS43–Code ''(Modified Monitored Sum 4B3T)'' eingesetzt. Hierbei handelt es sich um einen 4B3T–Code mit vier Codetabellen, die gemäß der laufenden digitalen Summe (nach $l$–Blöcken) |
:$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$ | :$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$ | ||
| − | zur Codierung herangezogen werden. Zur Initialisierung wird $\ | + | zur Codierung herangezogen werden. Zur Initialisierung wird ${\it \Sigma}_{0} = 0$ verwendet. |
| − | *Ändert sich die laufende digitale Summe nicht $(\ | + | |
| − | *Eine Zunahme $(\ | + | Die Farbgebungen in der Tabelle bedeuten: |
| + | *Ändert sich die laufende digitale Summe nicht $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, so ist ein Feld grau hinterlegt. | ||
| + | *Eine Zunahme $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ ist rot hinterlegt, eine Abnahme $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ blau. | ||
*Je intensiver die Farbgebung, um so größer ist die Änderung. | *Je intensiver die Farbgebung, um so größer ist die Änderung. | ||
| − | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/ | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Blockweise_Codierung_mit_4B3T-Codes|Blockweise Codierung mit 4B3T-Codes]]. |
| − | |||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Die Binärsymbole werden in diesem Lerntutorial mit '''L''' („Low”) und '''H''' („High”) bezeichnet. Häufig findet man in der Literatur auch die Binärsymbole '''L''' und '''0''' (statt '''H'''). Manchmal entspricht aber auch '''L''' unserem '''H''' und '''0''' dem '''L'''. | ||
| + | *Damit eine solche Verwirrung vermieden wird und die „0” nicht in beiden Alphabeten (binär und ternär) – dazu noch mit unterschiedlicher Bedeutung – auftritt, haben wir die zugegebenerweise etwas gewöhnungsbedürftige Nomenklatur verwendet. Wir sind uns durchaus bewusst, dass auch unsere Nomenklatur manche Leser verwirren wird. | ||
| + | *Sie können die Ergebnisse mit dem Interaktionsmodul [[Prinzip der 4B3T–Codierung]] überprüfen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Line 33: | Line 31: | ||
|type="[]"} | |type="[]"} | ||
- 4B3T ist immer besser als der redundanzfreie Binärcode. | - 4B3T ist immer besser als der redundanzfreie Binärcode. | ||
| − | + Das Sendesignal sollte wegen $H_{\rm K}(0) = 0$ gleichsignalfrei sein. | + | + Das Sendesignal sollte wegen $H_{\rm K}(f=0) = 0$ gleichsignalfrei sein. |
| − | + | + | +Eine kleinere Schrittgeschwindigkeit erlaubt größere Kabellänge. |
| − | {Codieren Sie die binäre Folge | + | {Codieren Sie die binäre Folge $\rm HHLL\hspace{0.08cm} LHLL\hspace{0.08cm} LHHL\hspace{0.08cm} HLHL$ (mit ${\it \Sigma}_{0} = 0$). <br>Wie lautet der Amplitudenkoeffizient des dritten Ternärsymbols des vierten Blocks? |
|type="{}"} | |type="{}"} | ||
$a_{12} \ = \ $ { -1.03--0.97 } | $a_{12} \ = \ $ { -1.03--0.97 } | ||
| − | {Ermitteln Sie das Markovdiagramm für den Übergang von $\ | + | {Ermitteln Sie das Markovdiagramm für den Übergang von ${\it \Sigma}_{l}$ auf ${\it \Sigma}_{l+1}$. Welche Übergangswahrscheinlichkeiten ergeben sich? |
|type="{}"} | |type="{}"} | ||
| − | $ {\Pr}(\ | + | $ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $ { 0.375 3% } |
| − | $ {\Pr}(\ | + | $ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $ { 0.1875 3% } |
| − | $ {\Pr}(\ | + | $ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ = \ $ { 0 3% } |
{Welche Eigenschaften folgen aus dem Markovdiagramm? | {Welche Eigenschaften folgen aus dem Markovdiagramm? | ||
|type="[]"} | |type="[]"} | ||
| − | - Gleiche Wahrscheinlichkeiten: Pr( | + | - Gleiche Wahrscheinlichkeiten: ${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}($\Sigma_{l} = 3)$. |
| − | + Es gilt Pr( | + | + Es gilt ${\rm Pr}({\it \Sigma}_{l} = 0) = {\rm Pr}({\it \Sigma}_{l} = 3)$ und ${\rm Pr}({\it \Sigma}_{l} = 1) = {\rm Pr}({\it \Sigma}_{l} = 2)$. |
| − | + Die Extremwerte ( | + | + Die Extremwerte $({\it \Sigma}_{l} = 0$ und ${\it \Sigma}_{l} = 3)$ treten seltener auf als die inneren Werte $({\it \Sigma}_{l} = 1$ und ${\it \Sigma}_{l} = 2)$. |
</quiz> | </quiz> | ||
Revision as of 12:20, 17 November 2017
Bei der ISDN–Datenübertragung wird in Deutschland und Belgien auf der so genannten $\rm {U_{K0}}$–Schnittstelle, die den Übertragungsweg zwischen Vermittlungsstelle und Wohnung beschreibt, der MMS43–Code (Modified Monitored Sum 4B3T) eingesetzt. Hierbei handelt es sich um einen 4B3T–Code mit vier Codetabellen, die gemäß der laufenden digitalen Summe (nach $l$–Blöcken)
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$
zur Codierung herangezogen werden. Zur Initialisierung wird ${\it \Sigma}_{0} = 0$ verwendet.
Die Farbgebungen in der Tabelle bedeuten:
- Ändert sich die laufende digitale Summe nicht $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, so ist ein Feld grau hinterlegt.
- Eine Zunahme $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ ist rot hinterlegt, eine Abnahme $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ blau.
- Je intensiver die Farbgebung, um so größer ist die Änderung.
Hinweise:
- Die Aufgabe gehört zum Kapitel Blockweise Codierung mit 4B3T-Codes.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Binärsymbole werden in diesem Lerntutorial mit L („Low”) und H („High”) bezeichnet. Häufig findet man in der Literatur auch die Binärsymbole L und 0 (statt H). Manchmal entspricht aber auch L unserem H und 0 dem L.
- Damit eine solche Verwirrung vermieden wird und die „0” nicht in beiden Alphabeten (binär und ternär) – dazu noch mit unterschiedlicher Bedeutung – auftritt, haben wir die zugegebenerweise etwas gewöhnungsbedürftige Nomenklatur verwendet. Wir sind uns durchaus bewusst, dass auch unsere Nomenklatur manche Leser verwirren wird.
- Sie können die Ergebnisse mit dem Interaktionsmodul Prinzip der 4B3T–Codierung überprüfen.
Fragebogen
Musterlösung
Die um $25 \%$ kleinere Schrittgeschwindigkeit $(1/T)$ des 4B3T–Codes gegenüber dem redundanzfreien Binärcode kommt ebenfalls den Übertragungseigenschaften von symmetrischen Kupferleitungen (starker Dämpfungsanstieg mit der Frequenz) entgegen. Bei gegebener Leitungsdämpfung lässt sich mit dem 4B3T–Code eine größere Länge überbrücken als mit einem redundanzfreien Binärsignal. Richtig sind also die Aussagen 2 und 3.
(2) Die 4B3T–Codierung ergibt mit dem Initialwert $\Sigma_{0} = 0$:
HHLL $\Rightarrow + + + (\Sigma_{1} = 3)$,\\
LHLL $\Rightarrow – + 0 (\Sigma_{2} = 3)$,
LHHL $\Rightarrow – – + (\Sigma_{3} = 2)$,
HLHL $\Rightarrow + – – (\Sigma_{4} = 1)$.
Der gesuchte Amplitudenkoeffizient ist somit $a_{12} = \underline{–1}$.
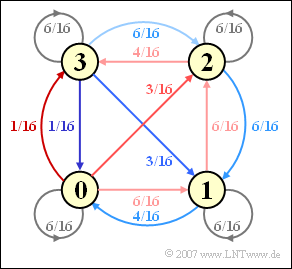
(3) Aus der Farbgebung der vorgegebenen Codetabelle kann das folgende Markovdiagramm ermittelt werden. Daraus kann man die gesuchten Übergangswahrscheinlichkeiten ablesen:
${\Pr}(\Sigma_{l+1} = 0 | \Sigma_{l} = 0) = 6/16 = 0.375,$ $ {\Pr}(\Sigma_{l+1} = 2 | \Sigma_{l} = 0)= 3/16 = 0.1875,$ $ {\Pr}(\Sigma_{l+1} = 0 | \Sigma_{l} = 2) = 0.$
(4) Die erste Aussage ist falsch, was man an den Asymmetrien im Markovdiagramm erkennt. Dagegen gibt es Symmetrien bezüglich der Zustände „$0$” und „$3$” sowie zwischen „$1$” und „$2$”. In der folgenden Berechnung schreiben wir anstelle von ${\Pr}(\Sigma_{l} = 0$ vereinfachend ${\Pr}(0)$. Unter Ausnutzung der Eigenschaft ${\Pr}(3) = {\Pr}(0)$ und ${\Pr}(2) = {\Pr}(1)$ ergeben sich aus dem Markovdiagramm folgende Gleichungen:
- $${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$
Aus der weiteren Bedingung ${\Pr}(0) + {\Pr}(1) = 1/2$ folgt weiter:
- $${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$
Diese Berechnung basiert auf der „Summe der ankommenden Pfeile im Zustand $0$”. Man könnte auch Gleichungen für die drei anderen Zustände angeben, die aber alle zum gleichen Ergebnis führen:
- $${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$
Richtig sind also die Aussagen 2 und 3.