Aufgaben:Exercise 1.2: ISDN and PCM

• Return to book

Komponenten eines PCM-Senders

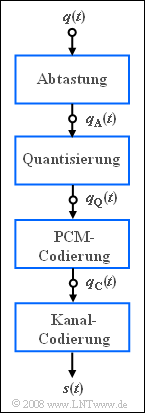
Die Umwandlung des analogen Sprachsignals $q(t)$ in das Binärsignal $q_{\rm C}(t)$ geschieht bei ISDN (Integrated Services Digital Network) entsprechend den Richtlinien der Pulscodemodulation (PCM) durch

• Abtastung im Abstand $T_{\rm A} = 1/f_{\rm A}$,
• Quantisierung auf $M = 256$ diskrete Werte,
• binäre PCM–Codierung mit $N \ \rm Bit$ pro Quantisierungswert.

Die Netto–Datenrate eines so genannten B–Kanals (Bearer Channel) ist $64 \ \rm kbit/s$ und entspricht der Bitrate des redundanzfreien Binärsignals $q_{\rm C}(t)$. Wegen der anschließenden redundanten Kanalcodierung und der eingefügten Signalisierungsbits ist allerdings die Brutto–Datenrate – also die Übertragungsrate des Sendesignals $s(t)$ – größer.

Ein Maß für die Qualität des gesamten (ISDN–)Übertragungssystems ist das Sinken–SNR

$$\rho_{\upsilon} = \frac{P_q}{P_{\epsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) -q(t)]^2}}$$

als das Verhältnis der Leistungen des auf den Bereich $300 \ {\rm Hz} ... 3400 \ {\rm Hz}$ bandbegrenzten Analogsignals $q(t)$ und des Fehlersignals $\varepsilon (t) = \upsilon (t) – q(t)$. Für das Sinkensignal $\upsilon (t)$ wird hierbei eine ideale Signalrekonstruktion mit einem idealen rechteckförmigen Tiefpass vorausgesetzt.

Hinweis:

Die Aufgabe bezieht sich auf Allgemeine Beschreibung von ISDN dieses Buches sowie auf Pulscodemodulation des Buches „Modulationsverfahren”.

Fragebogen

1

Mit wievielen Bit wird jeder (quantisierte) Abtastwert repräsentiert?

$N \ = \ $

2

Wie groß ist die Abtastrate?

$f_{\rm A} \ = \ $ $\ \rm kHz$

3

Ist damit das Abtasttheorem erfüllt?

	ja,
	nein.

4

Ist das Sinken–SNR ρυ bei ISDN durch folgende Effekte begrenzt?

	Abtastung (falls Abtasttheorem erfüllt),
	AWGN–Rauschen (Übertragungsfehler).

Musterlösung

Solution

(1)  Die Quantisierungsstufenzahl $M$ wird meist als Zweierpotenz gewählt und für die Bitanzahl $N = {\rm ld}(M)$. Aus $M = 2^{8} = 256$ folgt $\underline{N = 8}$.

(2)  Für die Bitrate gilt $R_{\rm B} = N \cdot f_{\rm A}$. Aus $R_{\rm B} = 64 \ \rm kbit/s$ und $N = 8$ erhält man somit $f_{\rm A} = 8 \ \rm kHz$.

(3)  Durch die Bandbegrenzung ist die höchste im Signal $q(t)$ enthaltene Frequenz gleich $3.4 \ \rm kHz$. Nach dem Abtasttheorem müsste deshalb $f_{\rm A} ≥ 6.8 \ \rm kHz$ gelten. Mit $f_{\rm A} = 8 \ \rm kHz$ ist die Bedingung erfüllt $\Rightarrow \underline {\rm JA}$.

(4)  Auch wenn der Einfluss des AWGN–Rauschens gering ist (kleine Rauschleistungsdichte $N_{0}$), kann das Sinken–SNR $\rho_{\upsilon}$ einen durch das Quantisierungsrauschen gegebenen Grenzwert nicht unterschreiten:

$$\rho_{\upsilon} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{\upsilon} \approx 48\, {\rm dB}\hspace{0.05cm}.$$

Bei größerer Rauschstörung wird $\rho_{\upsilon}$ durch die dann vorhandenen Übertragungsfehler weiter (signifikant) verringert. Dagegen führt die Abtastung zu keinem Qualitätsverlust, wenn das Abtasttheorem eingehalten wird. Die Abtastung kann dann vollständig rückgängig gemacht werden, wenn das Quellensignal $q(t)$ bandbegrenzt ist und die Signalrekonstruktion (ein idealer Tiefpass) richtig dimensioniert ist. Richtig sind somit die beiden letzten Aussagen.