Aufgaben:Exercise 1.3: Frame Structure of ISDN

• Return to book

Rahmenstruktur der S0-Schnittstelle

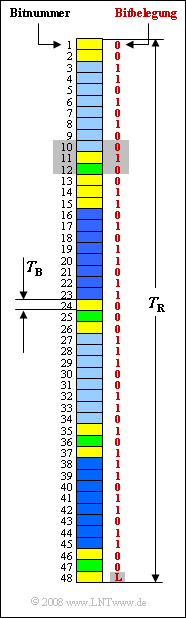
Die Grafik zeigt die Rahmenstruktur der $S_{0}$–Schnittstelle. Jeder Rahmen der Dauer $T_{\rm R}$ beinhaltet $48 \ \rm Bit$, darunter:

• $16 \ \rm Bit$ für den Bearer Channel B1 (hellblau),
• $16 \ \rm Bit$ für den Bearer Channel B2 (dunkelblau),
• $4 \ \rm Bit$ für den Data Channel D (grün).

Gelb eingezeichnet sind die erforderlichen Steuerbits.

Vorgegeben wird für diese Aufgabe, dass jeder der beiden Basiskanäle B1 und B2 eine Nettodatenrate von $R_{\rm B} = 64 \ \rm kbit/s$ bereitstellen soll.

Anzumerken ist noch, dass die Bitdauer $T_{\rm B}$ des uncodierten Binärsignals gleichzeitig die Symboldauer des (modifizierten) AMI–Codes angibt, der jede binäre „$1$” dem Spannungspegel $0 \ \rm V$ zuordnet und jede binäre „$0$” alternierend mit $+0.75 \ \rm V$ bzw. $–0.75 \ \rm V$ darstellt.

Die Zahlenwerte in der Grafik (rot markiert) geben eine Beispielfolge an, die in der Teilaufgabe (5) entsprechend dem modifizierten AMI–Code in Spannungspegel umgesetzt werden soll. Bitnummer $48$ beinhaltet das so genannte L–Bit. Dieses ist in der Teilaufgabe (6) so zu setzen, dass das Signal $s(t)$ gleichsignalfrei wird.

Hinweis:

Die Aufgabe bezieht sich auf ISDN-Basisanschluss dieses Buches. Der (modifizierte) AMI–Code wird ausführlich in Fourierreihe im Buch „Digitalsignalübertragung” beschrieben. Anzumerken ist ferner, dass die ersten $47 \ \rm Bit$ genau $22$ „Nullen” enthalten.

Fragebogen

1

Wie groß ist die Rahmendauer $T_{\rm R}$?

$T_{\rm R} \ = \ $ $\ \rm \mu s$

2

Wie groß ist die Bitdauer $T_{\rm B}$ (= Symboldauer nach der AMI–Codierung)?

$T_{\rm B} \ = \ $ $\ \rm \mu s $

3

Wie groß ist die Gesamt–Bruttodatenrate $R_{\rm ges}$?

$R_{\rm ges} \ = \ $ $\ \rm kbit/s$

4

Wieviele Steuerbits ($N_{\rm St}$) werden pro Rahmen übertragen?

$N_{\rm St} \ = \ $

5

Mit welchen Spannungswerten $(0 \ {\rm V}, +0.75 \ {\rm V}, –0.75 \ {\rm V})$ werden Bit $10, 11$ und $12$ (grau hinterlegter Block) dargestellt?

$U_{10} \ = \ $ $\ \rm V $

$U_{11} \ = \ $ $\ \rm V $

$U_{12} \ = \ $ $\ \rm V $

6

Welchen Spannungswert $(0 \ {\rm V}, ±0.75 \ {\rm V}) besitzt das L–Bit am Ende?

$U_{48} \ = \ $ $\ \rm V $

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)  (7)