Aufgaben:Exercise 3.6: State Transition Diagram

• Return to book

Einfacher Rate–1/2–Faltungscodierer

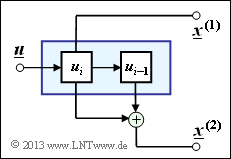
Eine Beschreibungsmöglichkeit für Faltungscodierer bietet das so genannte Zustandsübergangsdiagramm- Beinhaltet der Coder $m$ Speicherregister ⇒ Einflusslänge $\nu = m + 1$, so gibt es nach der aktuellen Speicherbelegung verschiedene Zustände $S_{\mu}$ mit $0 ≤ \mu ≤ 2^m \, –1$, wobei für den Index gilt:

$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$

Diese Art der Coderbeschreibung soll auf den oben skizzierten Faltungscodierer der Rate $R = 1/2$ angewendet werden.

Hinweis:

• Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm.

Fragebogen

1

Wieviele Zustände weist dieser Faltungscodierer auf?

${\rm Anzahl \ der \ Zustände} \ = \ $

2

Kommt man von jedem Zustand zu allen anderen Zuständen?

	Ja.
	Nein.

3

Welche Aussagen gelten für den Übergang von $s_i = S_1$ zu $s_{i+1} = S_0$?

	Das aktuelle Informationsbit muss $u_i = 0$ sein.
	Das aktuelle Informationsbit muss $u_i = 1$ sein.
	Die zugehörige Codesequenz lautet $\underline{x}_i = (01)$.
	Die zugehörige Codesequenz lautet $\underline{x}_i = (10)$.

4

Welche Aussagen gelten für den Übergang von $s_i = S_1$ zu $s_{i+1} = S_1$?

	Das aktuelle Informationsbit muss $u_i = 0$ sein.
	Das aktuelle Informationsbit muss $u_i = 1$ sein.
	Die zugehörige Codesequenz lautet $\underline{x}_i = (01)$.
	Die zugehörige Codesequenz lautet $\underline{x}_i = (10)$.

5

Welche Informationssequenzen sind möglich?

	$\underline{u} = (1, \, 1, \, 0, \, 0, \, 1 \, 1, \, ...)$,
	$\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \, ...)$.

6

Welche Codesequenzen sind möglich?

	$\underline{x} = (11, \, 10, \, 01, \, 00, \, 11, \, 10, \, ...)$,
	$\underline{x} = (11, \, 00, \, 10, \, 01, \, 11, \, 00, \, ...)$.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)