Aufgaben:Exercise 3.7: Comparison of Two Convolutional Encoders

• Return to book

Zwei $(n = 2, \ k = 1, \ m = 2)$–Faltungscodierer

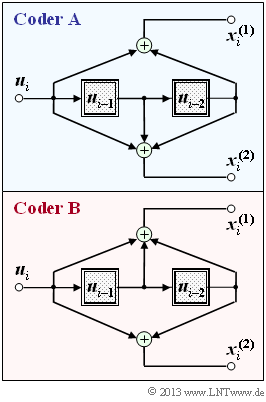
Die Grafik zeigt zwei Rate–1/2–Faltungscodierer, jeweils mit dem Gedächtnis $m = 2$:

• Der Coder A weist die Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$ auf.
• Beim Coder B sind die beiden Filter vertauscht, und es gilt : $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$.

Der untere Coder wurde im Theorieteil schon ausführlich behandelt. In der vorliegenden Aufgabe sollen Sie zunächst das Zustandsübergangsdiagramm für Coder A ermitteln und anschließend die Unterschiede und die Gemeinsamkeiten zwischen den beiden Diagrammen herausarbeiten.

Hinweis:

• Die Aufgabe bezieht sich auf die ersten Seiten des Kapitels Codebeschreibung mit Zustands– und Trellisdiagramm.

Fragebogen

1

Es gelte $\underline{u} = (0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, ...)$. Welche Sequenzen erzeugt Coder A?

	$\underline{x}^{(1)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, ...)$,
	$\underline{x}^{(1)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, ...)$,
	$\underline{x}^{(2)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, ...)$,
	$\underline{x}^{(2)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, ...)$.

2

Welche der genannten Zustandsübergänge gibt es bei Coder A?

	$s_i = S_0, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_0, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$.
	$s_i = S_1, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_1, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$.
	$s_i = S_2, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_2, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$.
	$s_i = S_3, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_3, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$.

3

Wie unterscheiden sich die beiden Zustandsübergangsdiagramme?

	Es sind andere Zustandsübergänge möglich.
	Bei allen acht Übergängen stehen andere Codesequenzen.
	Unterschiede gibt es nur für die Codesequenzen $(01)$ und $(10)$.

Musterlösung

Solution

(1) 

Berechnung der Codesequenz

Die Berechnung basiert auf den Gleichungen

• $x_i^{(1)} = u_i + u_{i–2}$,
• $x_i^{(2)} = u_i + u_{i–1} + u_{i–2}$.

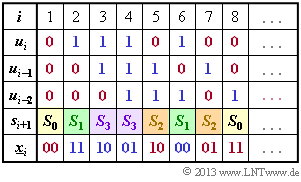
Zu Beginn sind die beiden Speicher ($u_{i–1} und $u_{i–2}$) mit Nullen vorbelegt  ⇒  $s_1 ) S_0$. Mit $u_1 = 0$ ergibt sich $\underline{x}_1 = (00)$ und $s_2 = S_0$. Mit $u_2 = 1$ erhält man die Ausgabe $\underline{x}_2 = (11)$ und den neuen Zustand $s_3 = S_3$. Aus nebenstehendem Berechnungsschema erkennt man die Richtigkeit der <u>Lösungsvorschläge 1 und 4</u>. '''(2)'''  Durch Auswertung der Tabelle von Teilaufgabe (1) erkennt man, dass <u>alle Aussagen</u> richtig sind. Die Ergebnisse sind in der folgenden Grafik dargestellt. [[File:P_ID2674__KC_A_3_7b.png|center|frame|Zustandsübergangsdiagramm für Coder A]] '''(3)'''  Nachfolgend sehen Sie das Zustandsübergangsdiagramm von Coder B, das bereits im Theorieteil auf [[Seite 2]] hergeleitet und interpretiert wurde. [[File:P_ID2675__KC_A_3_7c.png|Zustandsübergangsdiagramm für Coder B]] Richtig ist nur die <u>Aussage 3</u>. Vertauscht man die beiden Ausgabebits $x_i^{(1)}$ und $x_i^{(2)}$, so kommt man vom Faltungscodierer A zum Faltungscodierer B (und umgekehrt).