Aufgaben:Exercise 4.09: Recursive Systematic Convolutional Codes

• Return to book

Zustandsübergangsdiagramm eines RSC–Codes

In der Aufgabe A4.8 wurden bereits wichtige Eigenschaften von Faltungscodes aus dem Zustandsübergangsdiagramm abgeleitet, wobei von einer nichtrekursiven Filterstruktur ausgegangen wurde.

Nun wird ein Rate–1/2–RSC–Code in ähnlicher Weise behandelt. Hierbei steht „RSC” für „Recursive Systematic Convolutional”.

Die Übertragungsfunktionsmatrix eines RSC–Faltungscodes kann wie folgt angegeben werden:

$${\boldsymbol{\rm G}}(D) = \left [ 1\hspace{0.05cm},\hspace{0.3cm} G^{(2)}(D)/G^{(1)}(D) \right ] \hspace{0.05cm}.$$

Ansonsten gelten hier die genau gleichen Voraussetzungen wie bei Aufgabe A4.8. Wir verweisen wieder auf folgende Theorieseiten:

Systematische Faltungscodes (1)

Darstellung im Zustandsübergangsdiagramm (1)

Definition der freien Distanz (1)

GF(2)–Beschreibungsformen eines Digitalen Filters (2)

Anwendung der $D$–Transformation auf Rate–1/n–Faltungscodes (2)

Filterstruktur bei gebrochen–rationaler Übertragungsfunktion

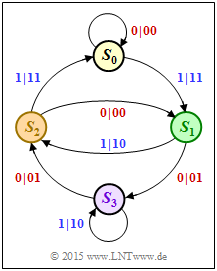
Im Zustandsübergangsdiagramm wird grundsätzlich vom Zustand $S_0$ ausgegangen. Von jedem Zustand gehen zwei Pfeile ab. Die Beschriftung lautet „$u_i | x_i^{(1)}x_i^{(2)}$”. Bei einem systematischen Code gilt dabei:

• Das erste Codebit ist identisch mit dem Informationsbit: $\hspace{0.2cm} x_i^{(1)} = u_i ∈ \{0, \, 1\}$.
• Das zweite Codebit ist das Prüfbit (Paritybit): $\hspace{0.2cm} x_i^{(2)} = p_i ∈ \{0, \, 1\}$.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Grundlegendes zu den Turbocodes.
• Ähnliche Aufgaben finden Sie in den Kapiteln 3.1 bis 3.3.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• In den Fragen zu dieser Aufgabe werden folgende vektoriellen Größen verwendet:
  • Informationssequenz: $\hspace{0.2cm} \underline{u} = (u_1, \, u_2, \, ...)$,
  • Paritysequenz: $\hspace{0.2cm} \underline{p} = (p_1, \, p_2, \, ...)$,
  • Impulsantwort: $\hspace{0.2cm} \underline{g} = (g_1, \, g_2, \, ...); \hspace{0.2cm}$ diese ist gleich der Paritysequenz $\underline{p}$ für $\underline{u} = (1, \, 0, \, 0, \, ...)$.

Fragebogen

1

Wie lautet die Impulsantwort $\underline{g}$?

	Es gilt $\underline{g} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \, ...)$.
	Es gilt $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, ...)$.

2

Es gelte $\underline{u} = (1, \, 1, \, 0, \, 1)$. Welche Aussagen gelten für die Paritysequenz $\underline{p}$?

	Es gilt $\underline{p} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, ...)$.
	Es gilt $\underline{p} = (1, \, 0, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, ...)$.
	Bei begrenzter Informationssequenz $\underline{u}$ ist stets auch $\underline{p}$ begrenzt.

3

Wie lautet die $D$–Übertragungsfunktion $G(D)$?

	Es gilt $G(D) = 1 + D + D^2 + D^4 + D^5 + D^7 + D^8 + \ ...$
	Es gilt $G(D) = (1 + D^2)/(1 + D + D^2)$.
	Es gilt $G(D) = (1 + D + D^2)/(1 + D^2)$.

4

Es gelte $\underline{u} = (1, \, 1, \, 1)$. Welche Aussagen gelten für die Paritysequenz $\underline{p}$?

	Es gilt $\underline{p} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, ...)$.
	Es gilt $\underline{p} = (1, \, 0, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, ...)$.
	Bei unbegrenzter Impulsantwort $\underline{g}$ ist stets auch $\underline{p}$ unbegrenzt.

5

Wie groß ist die freie Distanz dieses RSC–Coders?

$d_{\rm F} \ = \ $

Musterlösung

Solution

(1)  Verfolgt man die Übergänge im Zustandsdiagramm für die Sequenz $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0)$ am Eingang, so erhält man den Weg

$$S_0 → S_1 → S_3 → S_2 → S_1 → S_3 → S_2 → S_1 → S_3 \ ...$$

Bei jedem Übergang ist das erste Codesymbol $x_i^{(1)}$ gleich dem Informationsbit $u_i$ und das Codesymbol $x_i^{(2)}$ gibt das Paritybit $p_i$ an. Damit erhält man das Ergebnis entsprechend dem Lösungsvorschlag 1:

$$\underline{p}= (\hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) = \underline{g}\hspace{0.05cm}.$$

Bei einem jeden RSC–Code ist die Impulsantwort $\underline{g}$ unendlich lang und wird irgendwann periodisch, hier mit der Periode $P = 3$ und „$0, \, 1, \, 1$”.

(2)  Die Grafik zeigt die Lösung dieser Aufgabe entsprechend der Gleichung $\underline{p} = \underline{u}^{\rm T} \cdot \mathbf{G}$. Hierbei ist die Generatormatrix $\mathbf{G}$ nach unten und rechts unendlich weit ausgedehnt. Richtig ist der Lösungsvorschlag 2.

Verdeutlichung von $\underline{p} = (1, \, 1, \, 0, \, 1)^{\rm T} \cdot \mathbf{G}$

(3)  Zwischen der Impulsantwort $\underline{g}$ und der $D$–Übertragungsfunktion $\mathbf{G}(D)$ besteht der Zusammenhang

$$\underline{g}= (\hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}0\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}0\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, ... ) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1\hspace{-0.05cm}+\hspace{-0.05cm} D\hspace{-0.05cm} +\hspace{-0.05cm} D^2\hspace{-0.05cm} +\hspace{-0.05cm} D^4 \hspace{-0.05cm}+\hspace{-0.05cm} D^5 \hspace{-0.05cm}+\hspace{-0.05cm} D^7 \hspace{-0.05cm}+\hspace{-0.05cm} D^8 + ... \hspace{0.05cm}.$$

entsprechend dem ersten Lösungsvorschlag. Überprüfen wir nun den zweiten Vorschlag:

$$G(D) = \frac{1+ D^2}{1+ D + D^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G(D) \cdot [1+ D + D^2] = 1+ D^2 \hspace{0.05cm}.$$

Die folgende Rechnung zeigt, dass diese Gleichung tatsächlich stimmt:

$$(1+ D+ D^2+ D^4 +D^5 + D^7 + D^8 + ... ) \cdot (1+ D+ D^2 ) =$$

$$=1+ D+ D^2\hspace{1.05cm} +D^4 + D^5 \hspace{1.05cm} +D^7 + D^8 \hspace{1.05cm} + D^{10}+ ...$$

$$+ \hspace{0.8cm}D+ D^2+D^3 \hspace{1.05cm}+ D^5 + D^6 \hspace{1.05cm} +D^8 + D^9 \hspace{1.25cm} + ...$$

$$+ \hspace{1.63cm} D^2+D^3+ D^4 \hspace{1.05cm}+ D^6 +D^7 \hspace{1.05cm}+ D^9 + D^{10} \hspace{0.12cm}+ ...$$

$$=\underline{1\hspace{0.72 cm}+ D^2} \hspace{0.05cm}.$$

Richtig sind die Vorschläge 1 und 2. Da Gleichung (2) stimmt, muss die letzte Gleichung falsch sein.

(4)  Aus $\underline{u} = (1, \, 1, \, 1)$ folgt $U(D) = 1 + D + D^2$. Damit gilt auch:

$$P(D) = U(D) \cdot G(D) = (1+D+D^2) \cdot \frac{1+D^2}{1+D+D^2}= 1+D^2$$

$$\Rightarrow\hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm})\hspace{0.05cm}.$$

Richtig ist somit nur der Lösungsvorschlag 1. Insbesondere ist anzumerken:

• Wären die Größen $u_i$ und $g_i$ reellwertig, so würde die (diskrete) Faltung $\underline{p} = \underline{u} * \underline{g}$ stets zu einer Verbreiterung führen  ⇒  $\underline{p}$ wäre in diesem Fall breiter als $\underline{u}$ und auch breiter als $\underline{g}$.
• Bei $u_i ∈ {\rm GF}(2)$ und $g_i ∈ {\rm GF}(2)$ kann es (muss es aber nicht) dagegen vorkommen, dass auch bei unbegrenztem $\underline{u}$ oder bei unbegrenztem $\underline{g}$ das Faltungsprodukt $\underline{p} = \underline{u} * \underline{g}$ begrenzt ist.

Das Ergebnis wird nun noch entsprechend der Gleichung $\underline{p} = \underline{u}^{\rm T} \cdot \mathbf{G}$ überprüft.

Verdeutlichung von $\underline{p} = (1, \, 1, \, 1, \, 0, \, ...)^{\rm T} \cdot \mathbf{G}$

(5)  In ähnlicher Vorgehensweise wie in der Aufgabe A4.8, (4) wird auch hier die freie Distanz zum Beispiel durch den Pfad $S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \ ... \ $ bestimmt. Die zugehörige Codesequenz $\underline{x}$ ist nun aber „ $00 \ 11 \ 10 \ 11 \ 00 \ ...$”. Damit ergibt sich die freie Distanz zu $d_{\rm F} \ \underline{= 5}$. Beim nichtrekursiven Code von Aufgabe A4.8 wurde dagegen nur die freie Distanz $d_{\rm F} = 3$ ermittelt.