Difference between revisions of "Aufgaben:Exercise 4.11: Analysis of Parity-check Matrices"
From LNTwww
| Line 2: | Line 2: | ||
[[File:P_ID3067__KC_A_4_11_v2.png|right|frame|Produktcode und dessen Beschreibung durch die Prüfmatrix]] | [[File:P_ID3067__KC_A_4_11_v2.png|right|frame|Produktcode und dessen Beschreibung durch die Prüfmatrix]] | ||
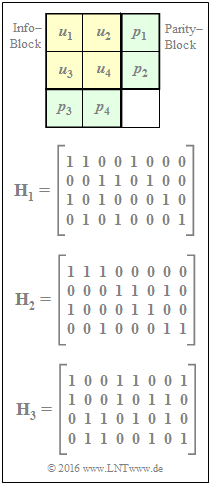
| + | In nebenstehender Grafik ist oben ein Produktcode angegeben, der durch folgende Prüfgleichungen gekennzeichnet ist: | ||
| + | :$$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},\hspace{0.3cm} | ||
| + | p_2 = u_3 \oplus u_4\hspace{0.05cm},$$ | ||
| + | :$$p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_3\hspace{0.05cm},\hspace{0.3cm} | ||
| + | p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$ | ||
| + | Darunter sind die Prüfmatrizen $\mathbf{H}_1, \ \mathbf{H}_2$ und $\mathbf{H}_3$ angegeben. Zu prüfen ist, welche der Matrizen den gegebenen Produktcode entsprechend der Gleichung $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ richtig beschreiben, wenn von folgenden Definitionen ausgegangen wird: | ||
| + | * dem Codewort $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$, | ||
| + | * dem Codewort $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$. | ||
| + | |||
| + | |||
| + | Alle $\mathbf{H}$–Matrizen beinhalten weniger Einsen als Nullen. Dies ist ein Kennzeichen der so genannten <i>Low–density Parity–check Codes</i> (kurz: LDPC–Codes). Bei den praxisrelevanten LDPC–Codes ist der Einsen–Anteil allerdings noch geringer als bei diesen Beispielen. | ||
| + | |||
| + | Weiterhin ist für die Aufgabe anzumerken: | ||
| + | * Ein $(n, \ k)$–Blockcode ist systematisch, wenn die ersten $k \ \rm Bit$ des Codewortes das Informationswort $\underline{u}$ beinhaltet. Mit der Codewortdefinition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ muss dann die Prüfmatrix $\mathbf{H}$ mit einer $k × k$–Diagonalmatrix enden. | ||
| + | * Ein <i>regulärer Code</i> (hinsichtlich LDPC–Anwendung) liegt vor, wenn das Hamming–Gewicht aller Zeilen ⇒ $w_{\rm Z}$ und das Hamming–Gewicht aller Spalten ⇒ $w_{\rm S}$ jeweils gleich ist. Andernfalls spricht man von einem <i>irregulären LDPC–Code</i>. | ||
Revision as of 13:38, 12 December 2017
In nebenstehender Grafik ist oben ein Produktcode angegeben, der durch folgende Prüfgleichungen gekennzeichnet ist:
- $$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},\hspace{0.3cm} p_2 = u_3 \oplus u_4\hspace{0.05cm},$$
- $$p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_3\hspace{0.05cm},\hspace{0.3cm} p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$
Darunter sind die Prüfmatrizen $\mathbf{H}_1, \ \mathbf{H}_2$ und $\mathbf{H}_3$ angegeben. Zu prüfen ist, welche der Matrizen den gegebenen Produktcode entsprechend der Gleichung $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ richtig beschreiben, wenn von folgenden Definitionen ausgegangen wird:
- dem Codewort $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$,
- dem Codewort $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
Alle $\mathbf{H}$–Matrizen beinhalten weniger Einsen als Nullen. Dies ist ein Kennzeichen der so genannten Low–density Parity–check Codes (kurz: LDPC–Codes). Bei den praxisrelevanten LDPC–Codes ist der Einsen–Anteil allerdings noch geringer als bei diesen Beispielen.
Weiterhin ist für die Aufgabe anzumerken:
- Ein $(n, \ k)$–Blockcode ist systematisch, wenn die ersten $k \ \rm Bit$ des Codewortes das Informationswort $\underline{u}$ beinhaltet. Mit der Codewortdefinition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ muss dann die Prüfmatrix $\mathbf{H}$ mit einer $k × k$–Diagonalmatrix enden.
- Ein regulärer Code (hinsichtlich LDPC–Anwendung) liegt vor, wenn das Hamming–Gewicht aller Zeilen ⇒ $w_{\rm Z}$ und das Hamming–Gewicht aller Spalten ⇒ $w_{\rm S}$ jeweils gleich ist. Andernfalls spricht man von einem irregulären LDPC–Code.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)