Difference between revisions of "Aufgaben:Exercise 1.16: Block Error Probability Bounds for AWGN"
| Line 11: | Line 11: | ||
*ein linearer Blockcode mit der Coderate $R = k/n$ und dem Distanzspektrum { $W_{i}$ }, $i = 1, ... , n,$ | *ein linearer Blockcode mit der Coderate $R = k/n$ und dem Distanzspektrum { $W_{i}$ }, $i = 1, ... , n,$ | ||
| − | *ein AWGN–Kanal, gekennzeichnet durch „$E_{\rm B}/N_{0}$” ⇒ umrechenbar in die Rauschleistung $\ | + | *ein AWGN–Kanal, gekennzeichnet durch „$E_{\rm B}/N_{0}$” ⇒ umrechenbar in die Rauschleistung $\sigma^2$, |
*ein Empfänger, basierend auf ''Soft Decision'' sowie dem ''Maximum–Likelihood–Kriterium''. | *ein Empfänger, basierend auf ''Soft Decision'' sowie dem ''Maximum–Likelihood–Kriterium''. | ||
| Line 21: | Line 21: | ||
Die Herleitung dieser Beziehung finden Sie in [Liv10]. In dieser Gleichung wurden verwendet: | Die Herleitung dieser Beziehung finden Sie in [Liv10]. In dieser Gleichung wurden verwendet: | ||
| − | *die komplementäre Gaußsche Fehlerfunktion Q( | + | *die komplementäre Gaußsche Fehlerfunktion ${\rm Q}(x)$, |
*das [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung|Hamming–Gewicht]] $w_{\rm H}(\underline{x}_{l})$ des Codewortes $\underline{x}_{l}$, | *das [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung|Hamming–Gewicht]] $w_{\rm H}(\underline{x}_{l})$ des Codewortes $\underline{x}_{l}$, | ||
| Line 33: | Line 33: | ||
:$$p_1 = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm},$$ | :$$p_1 = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm},$$ | ||
| − | *die so genannte Truncated Union Bound (TUB): | + | *die so genannte [http://www.eit.lth.se/fileadmin/eit/courses/ett051/Laborationer/Lab2ManualHt12009.pdf Truncated Union Bound] (TUB): |
:$$p_2 = W_{d_{\rm min}} \cdot {\rm Q}\left ( \sqrt{d_{\rm min}/\sigma^2} \right ) \hspace{0.05cm},$$ | :$$p_2 = W_{d_{\rm min}} \cdot {\rm Q}\left ( \sqrt{d_{\rm min}/\sigma^2} \right ) \hspace{0.05cm},$$ | ||
| − | *die Bhattacharyya–Schranke: | + | *die [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya|Bhattacharyya–Schranke:]] |
:$$p_3 = W(\beta) - 1\hspace{0.05cm},\hspace{0.2cm} {\rm mit}\hspace{0.15cm} \beta = {\rm exp}\left [ - 1/(2\sigma^2) \right ] \hspace{0.05cm}.$$ | :$$p_3 = W(\beta) - 1\hspace{0.05cm},\hspace{0.2cm} {\rm mit}\hspace{0.15cm} \beta = {\rm exp}\left [ - 1/(2\sigma^2) \right ] \hspace{0.05cm}.$$ | ||
| Line 45: | Line 45: | ||
:$$\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.$$ | :$$\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.$$ | ||
| − | Beim Übergang von der ''Union Bound'' $p_{1}$ zur Schranke $p_{3}$ wird unter Anderem die Funktion Q( | + | Beim Übergang von der ''Union Bound'' $p_{1}$ zur Schranke $p_{3}$ wird unter Anderem die Funktion ${\rm Q}(x)$ durch die ''Chernoff–Rubin–Schranke'' ${\rm Q}_{\rm CR}(x)$ ersetzt. Beide Funktionen sind in obigerer Grafik dargestellt (rote bzw. grüne Kurve). |
| − | In der Aufgabe | + | In der [[Aufgaben:1.16Z_Schranken_für_Q(x)|Aufgabe 1.16Z]] wird der Zusammenhang zwischen diesen Funktionen numerisch ausgewertet und Bezug genommen zu den Schranken ${\rm Q}_{o}(x)$ und ${\rm Q}_{u}(x)$, die in obiger Grafik ebenfalls eingezeichnet sind. |
| − | Hinweis: Die Aufgabe gehört zum Kapitel | + | |
| + | ''Hinweis:'' | ||
| + | |||
| + | Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit|Schranken für die Blockfehlerwahrscheinlichkeit]] Weiter verweisen wir auf folgendes Flash–Modul: | ||
Komplimentäre Gaußsche Fehlerfunktion (Dateigröße: 235 kB) | Komplimentäre Gaußsche Fehlerfunktion (Dateigröße: 235 kB) | ||
Revision as of 12:48, 14 December 2017
Wir gehen von der folgenden Konstellation aus:
- ein linearer Blockcode mit der Coderate $R = k/n$ und dem Distanzspektrum { $W_{i}$ }, $i = 1, ... , n,$
- ein AWGN–Kanal, gekennzeichnet durch „$E_{\rm B}/N_{0}$” ⇒ umrechenbar in die Rauschleistung $\sigma^2$,
- ein Empfänger, basierend auf Soft Decision sowie dem Maximum–Likelihood–Kriterium.
Unter der für die gesamte Aufgabe gültigen Annahme, dass stets das Nullwort $\underline{x}_{1} = (0, 0, ... , 0)$ gesendet wird, gilt für die „paarweise Fehlerwahrscheinlichkeit” mit einem anderen Codewort $\underline{x}_{l} (l = 2, ... , 2^k):$
- $$ {\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = {\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm}.$$
Die Herleitung dieser Beziehung finden Sie in [Liv10]. In dieser Gleichung wurden verwendet:
- die komplementäre Gaußsche Fehlerfunktion ${\rm Q}(x)$,
- das Hamming–Gewicht $w_{\rm H}(\underline{x}_{l})$ des Codewortes $\underline{x}_{l}$,
- die AWGN–Rauschleistung $\sigma^2 = (2 · R · E_{\rm B}/N_{0})^{–1}.$
Damit lassen sich verschiedene Schranken für die Blockfehlerwahrscheinlichkeit angeben:
- die sogenannte Union Bound:
- $$p_1 = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm},$$
- die so genannte Truncated Union Bound (TUB):
- $$p_2 = W_{d_{\rm min}} \cdot {\rm Q}\left ( \sqrt{d_{\rm min}/\sigma^2} \right ) \hspace{0.05cm},$$
- $$p_3 = W(\beta) - 1\hspace{0.05cm},\hspace{0.2cm} {\rm mit}\hspace{0.15cm} \beta = {\rm exp}\left [ - 1/(2\sigma^2) \right ] \hspace{0.05cm}.$$
In diesem Fall ist das Distanzspektrum { $W_{i}$ } durch die Gewichtsfunktion zu ersetzen:
- $$\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.$$
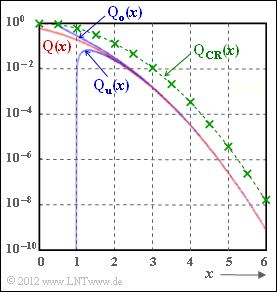
Beim Übergang von der Union Bound $p_{1}$ zur Schranke $p_{3}$ wird unter Anderem die Funktion ${\rm Q}(x)$ durch die Chernoff–Rubin–Schranke ${\rm Q}_{\rm CR}(x)$ ersetzt. Beide Funktionen sind in obigerer Grafik dargestellt (rote bzw. grüne Kurve).
In der Aufgabe 1.16Z wird der Zusammenhang zwischen diesen Funktionen numerisch ausgewertet und Bezug genommen zu den Schranken ${\rm Q}_{o}(x)$ und ${\rm Q}_{u}(x)$, die in obiger Grafik ebenfalls eingezeichnet sind.
Hinweis:
Die Aufgabe gehört zum Kapitel Schranken für die Blockfehlerwahrscheinlichkeit Weiter verweisen wir auf folgendes Flash–Modul:
Komplimentäre Gaußsche Fehlerfunktion (Dateigröße: 235 kB)
Fragebogen
Musterlösung