Difference between revisions of "Aufgaben:Exercise 4.7: About the Rake Receiver"

Revision as of 13:19, 18 December 2017

Zweiwegekanal und RAKE–Empfänger

Die Grafik zeigt einen Zweiwegekanal (gelbe Hinterlegung). Die entsprechende Beschreibungsgleichung lautet:

$$r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$

Die Verzögerung auf dem Nebenpfad sei $\tau = 1 \ \rm \mu s$. Darunter gezeichnet ist die Struktur eines RAKE–Empfängers (grüne Hinterlegung) mit den allgemeinen Koeffizienten $K, h_{0}, h_{1}, \tau_{0}$ und $\tau_{1}$.

Der RAKE–Empfänger hat die Aufgabe, die Energie der beiden Signalpfade zu bündeln und dadurch die Entscheidung sicherer zu machen. Die gemeinsame Impulsantwort von Kanal und RAKE–Empfänger kann in der Form

$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$

angegeben werden, allerdings nur dann, wenn die RAKE–Koeffizienten $h_{0}, h_{1}, \tau_{0}$ und $\tau_{1}$ geeignet gewählt werden. Der Hauptanteil von $h_{\rm KR}(t)$ soll bei $t = \tau$ liegen.

Die Konstante $K$ ist aus Normierungsgründen notwendig. Um den Einfluss von AWGN–Rauschen nicht zu verfälschen, muss folgende Bedingung erfüllt sein:

$$K= \frac{1}{h_0^2 + h_1^2}.$$

Gesucht sind außer den geeigneten RAKE–Parametern auch die Signale $r(t)$ und $b(t)$, wenn $s(t)$ ein Rechteck der Höhe $1$ und der Breite $T = 5 \ \rm \mu s$ ist.

Hinweis:

Die Aufgabe bezieht sich auf Nachrichtentechnische Aspekte von UMTS dieses Buches sowie auf Untersuchungen zum RAKE–Empfänger von Fehlerwahrscheinlichkeit der PN–Modulation im Buch „Modulationsverfahren”.

Fragebogen

Musterlösung

Solution

(1) (2) (3) (4) (5) (6) (7)

@@ Line 1: / Line 1: @@
-{{quiz-Header|Buchseite=Beispiele von Nachrichtensystemen/Nachrichtentechnische Aspekte von UMTS
+{{quiz-Header|Buchseite=Beispiele von Nachrichtensystemen/Nachrichtentechnische Aspekte von UMTS}}
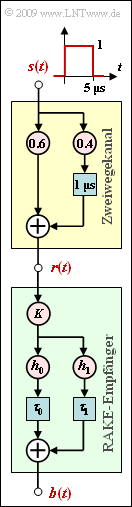
+[[File:P_ID1976__Mod_Z_5_5.png|right|frame|Zweiwegekanal und RAKE–Empfänger]]
-}}
+Die Grafik zeigt einen Zweiwegekanal (gelbe Hinterlegung). Die entsprechende Beschreibungsgleichung lautet:
-[[File:|right|frame|]]
+:$$r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$
+Die Verzögerung auf dem Nebenpfad sei $\tau = 1 \ \rm \mu s$. Darunter gezeichnet ist die Struktur eines RAKE–Empfängers (grüne Hinterlegung) mit den allgemeinen Koeffizienten $K, h_{0}, h_{1}, \tau_{0}$ und $\tau_{1}$.
+Der RAKE–Empfänger hat die Aufgabe, die Energie der beiden Signalpfade zu bündeln und dadurch die Entscheidung sicherer zu machen. Die gemeinsame Impulsantwort von Kanal und RAKE–Empfänger kann in der Form
+:$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$
+angegeben werden, allerdings nur dann, wenn die RAKE–Koeffizienten $h_{0}, h_{1}, \tau_{0}$ und $\tau_{1}$ geeignet gewählt werden. Der Hauptanteil von $h_{\rm KR}(t)$ soll bei $t = \tau$ liegen.
+Die Konstante $K$ ist aus Normierungsgründen notwendig. Um den Einfluss von AWGN–Rauschen nicht zu verfälschen, muss folgende Bedingung erfüllt sein:
+:$$K= \frac{1}{h_0^2 + h_1^2}.$$
+Gesucht sind außer den geeigneten RAKE–Parametern auch die Signale $r(t)$ und $b(t)$, wenn $s(t)$ ein Rechteck der Höhe $1$ und der Breite $T = 5 \ \rm \mu s$ ist.
+''Hinweis:''
+Die Aufgabe bezieht sich auf [[Beispiele_von_Nachrichtensystemen/Nachrichtentechnische_Aspekte_von_UMTS|Nachrichtentechnische Aspekte von UMTS]] dieses Buches sowie auf [[Modulationsverfahren/Fehlerwahrscheinlichkeit_der_PN–Modulation#Untersuchungen_zum_RAKE.E2.80.93Empf.C3.A4nger|Untersuchungen zum RAKE–Empfänger]] von [[Modulationsverfahren/Fehlerwahrscheinlichkeit_der_PN–Modulation|Fehlerwahrscheinlichkeit der PN–Modulation]] im Buch „Modulationsverfahren”.
 ===Fragebogen===

	Falsch
	Richtig