Difference between revisions of "Aufgaben:Exercise 2.11Z: Erasure Channel for Symbols"
| Line 2: | Line 2: | ||
[[File:P_ID2543__KC_Z_2_11.png|right|frame|Auslöschungskanal für Symbole: $m$–BEC]] | [[File:P_ID2543__KC_Z_2_11.png|right|frame|Auslöschungskanal für Symbole: $m$–BEC]] | ||
| − | Das Kanalmodell [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Erasure Channel]] (BEC) beschreibt einen Auslöschungskanal auf Bitebene. Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (<i>Erasure</i>) markiert. Im Gegensatz zum [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen. | + | Das Kanalmodell [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Erasure Channel]] (BEC) beschreibt einen Auslöschungskanal auf Bitebene. Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (<i>Erasure</i>) markiert. Im Gegensatz zum [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| BSC]] kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen. |
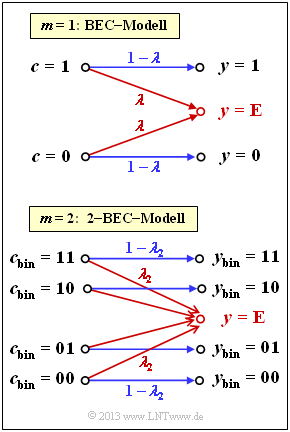
Ein Reed–Solomon–Code basiert auf einem Galoisfeld ${\rm GF}(2^m)$ mit ganzzahligem $m$. Jedes Codesymbol $c$ lässt sich somit durch $m \ \rm Bit$ darstellen. Will man hier das BEC–Modell anwenden, so muss man dieses zum <b><span style="color: rgb(204, 0, 0);"><i>m</i>–BEC–Modell</span></b> modifizieren, wie es in der unteren Grafik für $m = 2$ gezeigt ist: | Ein Reed–Solomon–Code basiert auf einem Galoisfeld ${\rm GF}(2^m)$ mit ganzzahligem $m$. Jedes Codesymbol $c$ lässt sich somit durch $m \ \rm Bit$ darstellen. Will man hier das BEC–Modell anwenden, so muss man dieses zum <b><span style="color: rgb(204, 0, 0);"><i>m</i>–BEC–Modell</span></b> modifizieren, wie es in der unteren Grafik für $m = 2$ gezeigt ist: | ||
Revision as of 10:45, 17 December 2017
Das Kanalmodell Binary Erasure Channel (BEC) beschreibt einen Auslöschungskanal auf Bitebene. Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (Erasure) markiert. Im Gegensatz zum BSC kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen.
Ein Reed–Solomon–Code basiert auf einem Galoisfeld ${\rm GF}(2^m)$ mit ganzzahligem $m$. Jedes Codesymbol $c$ lässt sich somit durch $m \ \rm Bit$ darstellen. Will man hier das BEC–Modell anwenden, so muss man dieses zum m–BEC–Modell modifizieren, wie es in der unteren Grafik für $m = 2$ gezeigt ist:
Alle Codesymbole – in binärer Darstellung $00, \ 01, \ 10$ und $11$ – werden mit der Wahrscheinlichkeit $1 - \lambda_2$ richtig übertragen. Damit beträgt die Wahrscheinlichkeit für ein ausgelöschtes Symbol $\lambda_2$. Zu beachten ist, dass bereits ein einziges ausgelöschtes Bit zum ausgelöschten Empfangssymbol $y = \rm E$ führt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Reed–Solomon–Decodierung beim Auslöschungskanal.
- Bei einem auf ${\rm GF}(2^m)$ basierenden Code ist das skizzierte 2–BEC–Modell zum $m$–BEC zu erweitern. Die Auslöschungswahrscheinlichkeit dieses Modell wird dann mit $\lambda_m$ bezeichnet.
- Für die Teilaufgaben (1), (2) und (3) gelte für die Auslöschungswahrscheinlichkeit des Grundmodells gemäß der oberen Grafik stets $\lambda = 0.2$.
Fragebogen
Musterlösung