Difference between revisions of "Aufgaben:Exercise 2.15Z: Block Error Probability once more"
From LNTwww
| Line 11: | Line 11: | ||
\sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$ | \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$ | ||
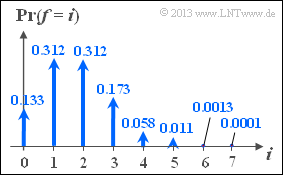
| − | In dieser Aufgabe soll die Blockfehlerwahrscheinlichkeit für den $\rm RSC \, (7, \, 3, \, 5)_8$ und verschiedene $\epsilon_{\rm S}$–Werte berechnet und | + | In dieser Aufgabe soll die Blockfehlerwahrscheinlichkeit für den $\rm RSC \, (7, \, 3, \, 5)_8$ und verschiedene $\epsilon_{\rm S}$–Werte berechnet und angenähert werden. Obige Gleichung erinnert an die [[Stochastische_Signaltheorie/Binomialverteilung|Biomialverteilung]]. Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung für die Parameter $n = 7$ (Codewortlänge) und $\epsilon_{\rm S} = 0.25$ (Symbolverfälschungswahrscheinlichkeit). |
''Hinweise:'' | ''Hinweise:'' | ||
Revision as of 13:11, 19 December 2017
Bei Verwendung eines Reed–Solomon–Codes mit der Korrekturfähigkeit $t$ und Bounded Distance Decoding (BDD) erhält man mit
- der Codewortlänge $n$ und
- der Symbolverfälschungswahrscheinlichkeit $\epsilon_{\rm S}$
für die Blockfehlerwahrscheinlichkeit:
- $${\rm Pr(Blockfehler)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$
In dieser Aufgabe soll die Blockfehlerwahrscheinlichkeit für den $\rm RSC \, (7, \, 3, \, 5)_8$ und verschiedene $\epsilon_{\rm S}$–Werte berechnet und angenähert werden. Obige Gleichung erinnert an die Biomialverteilung. Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung für die Parameter $n = 7$ (Codewortlänge) und $\epsilon_{\rm S} = 0.25$ (Symbolverfälschungswahrscheinlichkeit).
Hinweise:
- Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit und Anwendungsgebiete.
- Zur Kontrolle können Sie das folgende interaktive Flash–Modul nutzen:
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)