Difference between revisions of "Aufgaben:Exercise 3.4Z: Continuous Phase Frequency Shift Keying"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Beispiele von Nachrichtensystemen/Funkschnittstelle }} [[File:|right|frame|]] ===Fragebogen=== <quiz display=simple> {Multiple-C…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|frame|]] | + | [[File:P_ID1231__Bei_Z_3_4.png|right|frame|Continuous Phase FSK]] |
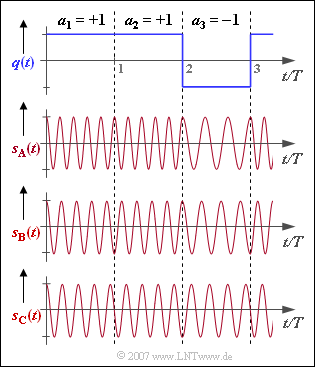
| + | Die Grafik zeigt drei FSK–Sendesignale, die sich hinsichtlich Frequenzhub $\Delta f_{\rm A}$ und somit auch durch ihren Modulationsindex | ||
| + | :$$h = 2 \cdot \Delta f_{\rm A} \cdot T$$ | ||
| + | unterscheiden. Das digitale Quellensignal $q(t)$, das den Signalen $s_{\rm A}(t), s_{\rm B}(t)$ und $s_{\rm C}(t)$ zugrundeliegt, ist oben dargestellt. Alle betrachteten Signale sind auf die Amplitude $1$ und die Zeitdauer $T$ normiert und basieren auf einem Cosinusträger mit der Frequenz $f_{\rm T}$. | ||
| + | Bei binärer FSK (''Binary Frequency Shift Keying'') treten bitweise nur zwei verschiedene Frequenzen | ||
| + | *$f_{1}$ (falls $a_{\nu} = +1$) und | ||
| + | *$f_{2}$ (falls $a_{\nu} = –1$) | ||
| + | auf. Ist der Modulationsindex kein Vielfaches von $2$, so ist eine kontinuierliche Phasenanpassung erforderlich, um Phasensprünge zu vermeiden. | ||
| + | Ein wichtiger Sonderfall stellt die binäre FSK mit dem Modulationsindex $h = 0.5$ dar, die auch als $\color{red}{\rm Minimum \ Shift \ Keying}$ (MSK) bezeichnet wird. Diese wird in dieser Aufgabe eingehend behandelt. | ||
| + | |||
| + | |||
| + | ''Hinweis:'' | ||
| + | |||
| + | Diese Aufgabe gehört zum [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle|Funkschnittstelle]]. Die hier behandelte Thematik findet sich in dem nachfolgend aufgeführten Interaktionsmodul: | ||
| + | [[Frequency Shift Keying und CPM]] | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 17:03, 19 December 2017
Die Grafik zeigt drei FSK–Sendesignale, die sich hinsichtlich Frequenzhub $\Delta f_{\rm A}$ und somit auch durch ihren Modulationsindex
- $$h = 2 \cdot \Delta f_{\rm A} \cdot T$$
unterscheiden. Das digitale Quellensignal $q(t)$, das den Signalen $s_{\rm A}(t), s_{\rm B}(t)$ und $s_{\rm C}(t)$ zugrundeliegt, ist oben dargestellt. Alle betrachteten Signale sind auf die Amplitude $1$ und die Zeitdauer $T$ normiert und basieren auf einem Cosinusträger mit der Frequenz $f_{\rm T}$.
Bei binärer FSK (Binary Frequency Shift Keying) treten bitweise nur zwei verschiedene Frequenzen
- $f_{1}$ (falls $a_{\nu} = +1$) und
- $f_{2}$ (falls $a_{\nu} = –1$)
auf. Ist der Modulationsindex kein Vielfaches von $2$, so ist eine kontinuierliche Phasenanpassung erforderlich, um Phasensprünge zu vermeiden.
Ein wichtiger Sonderfall stellt die binäre FSK mit dem Modulationsindex $h = 0.5$ dar, die auch als $\color{red}{\rm Minimum \ Shift \ Keying}$ (MSK) bezeichnet wird. Diese wird in dieser Aufgabe eingehend behandelt.
Hinweis:
Diese Aufgabe gehört zum Funkschnittstelle. Die hier behandelte Thematik findet sich in dem nachfolgend aufgeführten Interaktionsmodul: Frequency Shift Keying und CPM
Fragebogen
Musterlösung