Aufgaben:Exercise 2.16: Bounded Distance Decoding: Decision Regions

• Return to book

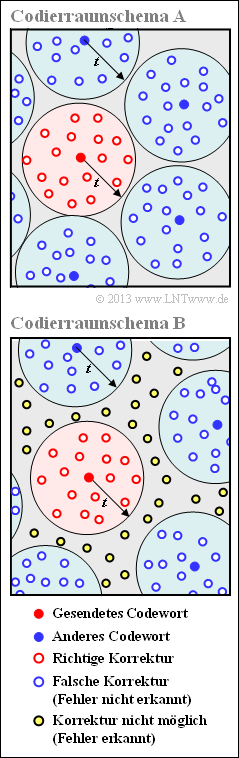
Wir gehen von einem Blockcode der Länge $n$ mit Symbolen $c_i ∈ {\rm GF}(2^m)$ aus, der bis zu $t$ Symbole korrigieren kann. Jedes mögliche Empfangswort $\underline{y}_i$ kann dann als ein Punkt in einem hochdimensionalen Raum angesehen werden. Geht man von der Basis ${\rm GF}(2) = \{0, \, 1\}$ aus, so beträgt die Dimension $n \cdot m$.

Die Grafik zeigt einen solchen Raum in stark vereinfachender 2D–Darstellung. Die Abbildung ist wie folgt zu interpretieren:

• Gesendet wurde der rote Punkt $\underline{c}_j$. Alle rot umrandeten Punkte $\underline{y}_i$ in einer Hyperkugel um diesen Punkt $\underline{c}_j$ mit dem Parameter $t$ als Radius können korrigiert werden. Mit der Nomenklatur gemäß der Grafik im Theorieteil gilt dann $\underline{z}_i = \underline{c}_j$  ⇒  „Die Fehlerkorrektur ist erfolgreich”.

• Bei sehr vielen Symbolfehlern kann $\underline{c}_j$ in einen blauen (oder weißblauen) Punkt $\underline{y}_j$ verfälscht werden, der zur Hyperkugel eines anderen Codewortes $\underline{c}_{k ≠ j}$ gehört. In diesem Fall trifft der Decoder eine falsche Entscheidung  ⇒  „Das Empfangswort $\underline{y}_j$ wird falsch decodiert”.

• Schließlich kann es wie in der unteren Skizze auch noch gelbe Punkte geben, die zu keiner Hyperkugel gehören  ⇒  „Das Empfangswort $\underline{y}_j$ ist nicht decodierbar”.

In dieser Aufgabe sollen Sie entscheiden, welches der beiden Coderaumschemata geeignet ist zur Beschreibung der

• BDD–Decodierung von Hamming–Codes bzw.
• BDD–Decodierung von Reed–Solomon–Codes.

Hinweis:

• Die Aufgabe ergänzt die Thematik des Kapitels Fehlerwahrscheinlichkeit und Anwendungsgebiete und soll signifikante Unterschiede bei der Decodierung von Reed–Solomon–Codes und Hamming–Codes verdeutlichen.

Fragebogen

1

Welches Codierraumschema trifft für die Hamming–Codes zu?

	Codierraumschema $\mathbf{A}$,
	Codierraumschema $\mathbf{B}$.

2

Welche Aussage gilt für die Wahrscheinlichkeit, dass bei Hamming–Codierung ein Empfangswort $\underline{y}$ nicht decodiert werden kann?

	Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist exakt $0$.
	${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist ungleich $0$, aber vernachlässigbar.
	Es gilt ${\rm Pr}(\underline{y} {\rm \ ist \ nicht \ decodierbar}) > {\rm Pr}(\underline{y} \rm \ wird \ falsch \ decodiert)$.

3

Welches Codierraumschema trifft für die Reed–Solomon–Codes zu?

	Codierraumschema $\mathbf{A}$,
	Codierraumschema $\mathbf{B}$.

4

Welche Aussage gilt für die Wahrscheinlichkeit, dass ein Empfangswort $\underline{y}$ nach Reed–Solomon–Codierung nicht decodiert werden kann?

	Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist exakt $0$.
	${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist ungleich $0$, aber vernachlässigbar.
	Es gilt ${\rm Pr}(\underline{y} {\rm \ ist \ nicht \ decodierbar}) > {\rm Pr}(\underline{y} \rm \ wird \ falsch \ decodiert)$.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)