Aufgaben:Exercise 3.4Z: Trapezoid, Rectangle and Triangle

• Return to book

Trapezimpuls und die Grenzfälle „Rechteck” und „Dreieck”

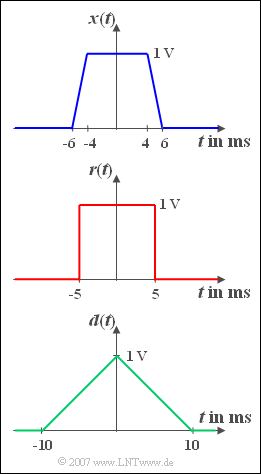
Betrachtet werden drei unterschiedliche Impulsformen. Der Impuls ${x(t)}$ ist trapezförmig. Für $| t | < t_1 = 4 \,\text{ms}$ ist der Zeitverlauf konstant ${A} = 1\, \text{V}$. Danach fällt ${x(t)}$ bis zum Zeitpunkt $t_2 = 6\, \text{ms}$ linear bis auf den Wert $0$ ab.

Mit den beiden abgeleiteten Systemgrößen, nämlich

• der äquivalenten Impulsdauer

$$\Delta t = t_1 + t_2$$

• und dem so genannten Rolloff-Faktor (im Zeitbereich)

$$r_t = \frac{t_2 - t_1 }{t_2 + t_1 }$$

lautet die Spektralfunktion des Trapezimpulses:

$$X( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits}( {{\rm \pi} \cdot \Delta t \cdot f} ) \cdot \hspace{0.1cm}{\mathop{\rm si}\nolimits}( {{\rm \pi}\cdot \Delta t \cdot r_t \cdot f} ).$$

Weiter sind in der Grafik noch der Rechteckimpuls ${r(t)}$ und der Dreieckimpuls ${d(t)}$ dargestellt, die beide als Grenzfälle des Trapezimpulses ${x(t)}$ interpretiert werden können.

Hinweise:

• Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Sie können Ihre Ergebnisse anhand der beiden interaktiven Applets Impulse und Spektren sowie Frequenzgang und Impulsantwort überprüfen.

Fragebogen

1

Wie groß sind die äquivalente Impulsdauer und der Rolloff-Faktor von ${x(t)}$?

$\Delta t \ = \ $  $\text{ms}$

$r_t\hspace{0.3cm} = \ $

2

Welche Aussagen sind hinsichtlich der Spektralfunktion ${X(f)}$ zutreffend?

	Der Spektralwert bei der Frequenz $f = 0$ ist gleich $20 \,\text{mV/Hz}$.
	Für die Phasenfunktion sind die Werte $0$ oder $\pi$ ($180^{\circ}$) möglich.
	${X(f)}$ weist nur Nullstellen bei allen Vielfachen von $100 \,\text{Hz}$ auf.

3

Welche Aussagen sind hinsichtlich der Spektralfunktion ${R(f)}$ zutreffend?

	Der Spektralwert bei der Frequenz $f = 0$ ist gleich ${X(f = 0)}$.
	Für die Phasenfunktion sind die Werte $0$ oder $\pi$ ($180^{\circ}$) möglich.
	${R(f)}$ weist nur Nullstellen bei allen Vielfachen von $100 \,\text{Hz}$ auf.

4

Welche Aussagen sind hinsichtlich der Spektralfunktion ${D(f)}$ zutreffend?

	Der Spektralwert bei der Frequenz $f = 0$ ist gleich ${X(f = 0)}$.
	Für die Phasenfunktion sind die Werte $0$ oder $\pi$ ($180^{\circ}$) möglich.
	${D(f)}$ weist nur Nullstellen bei allen Vielfachen von $100 \,\text{Hz}$ auf.

Musterlösung

Solution

1. Die äquivalente Impulsdauer ist $\Delta t = t_1 + t_2 \;\underline{= 10 \,\text{ms}}$ und der Rolloff-Faktor $r_t = 2/10 \;\underline{= 0.2}$.

2. Richtig sind die Lösungsvorschläge 2 und 3:

• Der Spektralwert bei $f = 0$ beträgt $A \cdot \Delta t = 10 \,\text{mV/Hz}$.
• Da ${X(f)}$ reell ist und sowohl positive als auch negative Werte annehmen kann, sind nur die zwei Phasenwerte $0$ und $\pi$ möglich.
• Nullstellen gibt es aufgrund der ersten si-Funktion bei allen Vielfachen von $1/\Delta t = 100\, \text{Hz}$.
• Die zweite si-Funktion führt zu Nulldurchgängen im Abstand $1/(r_t \cdot \Delta t) = 500 \,\text{Hz}$. Diese fallen exakt mit den Nullstellen der ersten si-Funktion zusammen.

3. Alle Lösungsvorschläge sind zutreffend:

• Mit der äquivalenten Impulsdauer $\Delta t = 10 \,\text{ms}$ und dem Rolloff-Faktor $r_t = 0$ erhält man:   $R( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }} \cdot \Delta t \cdot f} ).$

4. Hier sind die Lösungsvorschläge 1 und 3 zutreffend:

• Beim Dreieckimpuls ist der Rolloff-Faktor $r_t = 1$.
• Die äquivalente Impulsdauer ist ebenfalls $\Delta t = 10 \,\text{ms}$. Daraus folgt   $D( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }} \cdot \Delta t \cdot f} ).$
• Da ${D(f)}$ nicht negativ werden kann, ist die Phase $[{\rm arc} \; {D(f)}]$ stets $0$. Der Phasenwert $\pi$ ($180°$) ist also bei der Dreieckform nicht möglich.