Difference between revisions of "Aufgaben:Exercise 3.2: Laplace Transform"
m (Guenter verschob die Seite 3.2 Laplace-Transformation nach Aufgabe 3.2: Laplace-Transformation) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
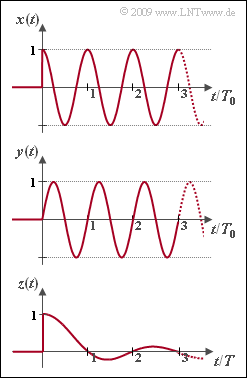
| − | [[File:P_ID1763__LZI_A_3_2.png|right| | + | [[File:P_ID1763__LZI_A_3_2.png|right|frame|Drei kausale Zeitfunktionen]] |
Kausale Signale und Systeme beschreibt man meist mittels der Laplace–Transformation. Ist $x(t)$ für alle Zeiten $t < 0$ identisch $0$, so lautet die Laplace–Transformierte: | Kausale Signale und Systeme beschreibt man meist mittels der Laplace–Transformation. Ist $x(t)$ für alle Zeiten $t < 0$ identisch $0$, so lautet die Laplace–Transformierte: | ||
| − | $$X_{\rm L}(p) = \int_{0}^{ | + | :$$X_{\rm L}(p) = \int_{0}^{ |
\infty} | \infty} | ||
{ x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm | { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm | ||
d}t\hspace{0.05cm}\hspace{0.05cm} .$$ | d}t\hspace{0.05cm}\hspace{0.05cm} .$$ | ||
| − | In dieser Aufgabe sollen die Laplace–Transformierten der in der Grafik dargestellten kausalen Signale ermittelt werden. Die folgenden Gleichungen gelten jeweils nur für $t \ge 0$. Für negative Zeiten sind alle Signale identisch | + | In dieser Aufgabe sollen die Laplace–Transformierten der in der Grafik dargestellten kausalen Signale ermittelt werden. Die folgenden Gleichungen gelten jeweils nur für $t \ge 0$. Für negative Zeiten sind alle Signale identisch Null. |
*Cosinussignal mit der Periodendauer $T_0$: | *Cosinussignal mit der Periodendauer $T_0$: | ||
| Line 18: | Line 18: | ||
:$$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$ | :$$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$ | ||
| − | *$\sin(t | + | *$\sin(t)/t$–Signal mit äquivalenten Nulldurchgängen im Abstand $T$: |
:$$z(t) = {\rm si} (\pi \cdot {t}/{T})\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x | :$$z(t) = {\rm si} (\pi \cdot {t}/{T})\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Da $z(t)$ ebenso wie die anderen hier betrachteten Signale $x(t)$ und $y(t)$ nicht energiebegrenzt ist, kann zur Berechnung der Spektralfunktion nicht die folgende Gleichung herangezogen werden: | + | Da $z(t)$ ebenso wie die anderen hier betrachteten Signale $x(t)$ und $y(t)$ nicht energiebegrenzt ist, kann zur Berechnung der Spektralfunktion <u>nicht</u> die folgende Gleichung herangezogen werden: |
:$$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it | :$$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it | ||
f}} .$$ | f}} .$$ | ||
| − | Vielmehr ist zu berücksichtigen, dass $z(t) = s(t) \cdot \gamma(t)$ gilt, wobei $s(t)$ hier die herkömmliche symmetrische si–Funktion bezeichnet: | + | Vielmehr ist zu berücksichtigen, dass $z(t) = s(t) \cdot \gamma(t)$ gilt, wobei $s(t)$ hier die herkömmliche symmetrische $\rm si$–Funktion bezeichnet: |
:$$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad | :$$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad | ||
\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f)$$ | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f)$$ | ||
| Line 36: | Line 36: | ||
$S(f)$ ist eine um $f = 0$ symmetrische Rechteckfunktion mit der Höhe $T$ und der Breite $1/T$. | $S(f)$ ist eine um $f = 0$ symmetrische Rechteckfunktion mit der Höhe $T$ und der Breite $1/T$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion|Laplace–Transformation und p–Übertragungsfunktion]]. | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion|Laplace–Transformation und p–Übertragungsfunktion]]. | ||
| − | |||
*Gegeben sind folgende bestimmte Integrale: | *Gegeben sind folgende bestimmte Integrale: | ||
:$$\int_{0}^{ | :$$\int_{0}^{ | ||
| Line 56: | Line 61: | ||
{ \frac{1}{x}}\hspace{0.1cm}{\rm | { \frac{1}{x}}\hspace{0.1cm}{\rm | ||
d}x = {\rm ln}\hspace{0.15cm}\frac{B}{A}\hspace{0.05cm} .$$ | d}x = {\rm ln}\hspace{0.15cm}\frac{B}{A}\hspace{0.05cm} .$$ | ||
| + | |||
| + | |||
| Line 74: | Line 81: | ||
| − | {Berechnen Sie die Laplace–Transformierte $Z_{\rm L}(p)$ der kausalen si–Funktion $z(t)$. Wie lautet die richtige Lösung? | + | {Berechnen Sie die Laplace–Transformierte $Z_{\rm L}(p)$ der kausalen $\rm si$–Funktion $z(t)$. Wie lautet die richtige Lösung? |
|type="[]"} | |type="[]"} | ||
- $Z_{\rm L}(p)$ hat einen rechteckförmigen Verlauf. | - $Z_{\rm L}(p)$ hat einen rechteckförmigen Verlauf. | ||
| − | - | + | - $Z_{\rm L}(p) = \arctan (1/p)$. |
| − | + | + | + $Z_{\rm L}(p) = T/\pi \cdot \arctan (\pi/(pT))$. |
{Berechnen Sie den Realteil des Spektrums $Z(f)$. Welche Aussagen treffen zu? | {Berechnen Sie den Realteil des Spektrums $Z(f)$. Welche Aussagen treffen zu? | ||
| − | |type=" | + | |type="()"} |
+ ${\rm Re}[Z(f)]$ hat einen rechteckförmigen Verlauf. | + ${\rm Re}[Z(f)]$ hat einen rechteckförmigen Verlauf. | ||
- ${\rm Re}[Z(f)]$ ist proportional zu $\ln\; |(f \cdot T -0.5)/(f \cdot T +0.5)|.$ | - ${\rm Re}[Z(f)]$ ist proportional zu $\ln\; |(f \cdot T -0.5)/(f \cdot T +0.5)|.$ | ||
| Line 88: | Line 95: | ||
{Berechnen Sie den Imaginärteil von $Z(f)$. Welche Aussagen treffen zu? | {Berechnen Sie den Imaginärteil von $Z(f)$. Welche Aussagen treffen zu? | ||
| − | |type=" | + | |type="()"} |
- ${\rm Im}[Z(f)]$ hat einen rechteckförmigen Verlauf. | - ${\rm Im}[Z(f)]$ hat einen rechteckförmigen Verlauf. | ||
+ ${\rm Im}[Z(f)]$ ist proportional zu $\ln\; |(f \cdot T -0.5)/(f \cdot T +0.5)|.$ | + ${\rm Im}[Z(f)]$ ist proportional zu $\ln\; |(f \cdot T -0.5)/(f \cdot T +0.5)|.$ | ||
Revision as of 16:33, 15 March 2018
Kausale Signale und Systeme beschreibt man meist mittels der Laplace–Transformation. Ist $x(t)$ für alle Zeiten $t < 0$ identisch $0$, so lautet die Laplace–Transformierte:
- $$X_{\rm L}(p) = \int_{0}^{ \infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}\hspace{0.05cm} .$$
In dieser Aufgabe sollen die Laplace–Transformierten der in der Grafik dargestellten kausalen Signale ermittelt werden. Die folgenden Gleichungen gelten jeweils nur für $t \ge 0$. Für negative Zeiten sind alle Signale identisch Null.
- Cosinussignal mit der Periodendauer $T_0$:
- $$x(t) = {\rm cos} (2\pi \cdot {t}/{T_0})= {\rm cos} (\omega_0 \cdot t) \hspace{0.05cm},$$
- Sinussignal mit Periodendauer $T_0$:
- $$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$
- $\sin(t)/t$–Signal mit äquivalenten Nulldurchgängen im Abstand $T$:
- $$z(t) = {\rm si} (\pi \cdot {t}/{T})\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x \hspace{0.05cm}.$$
Da $z(t)$ ebenso wie die anderen hier betrachteten Signale $x(t)$ und $y(t)$ nicht energiebegrenzt ist, kann zur Berechnung der Spektralfunktion nicht die folgende Gleichung herangezogen werden:
- $$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} .$$
Vielmehr ist zu berücksichtigen, dass $z(t) = s(t) \cdot \gamma(t)$ gilt, wobei $s(t)$ hier die herkömmliche symmetrische $\rm si$–Funktion bezeichnet:
- $$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f)$$
Die Fouriertansformierte der Sprungfunktion $\gamma(t)$ lautet:
- $$\gamma(t) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad \Gamma(f) = {1}/{2} \cdot \delta (f) + \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$
$S(f)$ ist eine um $f = 0$ symmetrische Rechteckfunktion mit der Höhe $T$ und der Breite $1/T$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.
- Gegeben sind folgende bestimmte Integrale:
- $$\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \cos(qx)}\hspace{0.1cm}{\rm d}x = \frac{p}{p^2 + q^2}\hspace{0.05cm} , \hspace{1.0cm}\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \sin(qx)}\hspace{0.1cm}{\rm d}x = \frac{q}{p^2 + q^2}\hspace{0.05cm} , $$
- $$\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \frac{\sin(qx)}{x}}\hspace{0.1cm}{\rm d}x = {\rm arctan}\hspace{0.15cm}\frac{q}{p}\hspace{0.05cm} , \hspace{0.6cm} \int_{A}^{ B} { \frac{1}{x}}\hspace{0.1cm}{\rm d}x = {\rm ln}\hspace{0.15cm}\frac{B}{A}\hspace{0.05cm} .$$
Fragebogen
Musterlösung
Richtig ist somit der Vorschlag 2.
- Der Vorschlag 3 scheitert von vorneherein aus, da $X_{\rm L}(p)$ die Einheit „Sekunde” aufweisen muss (Integral über die Zeit), während $p$ und $\omega_0$ jeweils die Einheit „1/s” besitzen.
(2) Hier gilt bei gleicher Vorgehensweise wie in der Teilaufgabe (1):
$$Y_{\rm L}(p) = \int_{0}^{
\infty}
{ {\rm sin} (\omega_0 \cdot T) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm
d}t = \frac{\omega_0}{p^2 + \omega_0^2}
\hspace{0.05cm} .$$
Richtig ist somit der Lösungsvorschlag 1.
(3) Die $p$–Übertragungsfunktion der kausalen si–Funktion lautet mit dem vorne angegebenen Integral:
$$Z_{\rm L}(p) = \int_{0}^{
\infty}
{ \frac{\sin(\pi \cdot t/T)}{\pi \cdot t/T} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm
d}t = \frac{T}{\pi} \cdot {\rm arctan} \; \frac{\pi}{p\cdot T}
\hspace{0.05cm} .$$
Richtig ist somit der Lösungsvorschlag 3
- Der Vorschlag 1 gilt nur für die Fouriertransformierte der akausalen si–Funktion.
- Der Vorschlag 2 kann schon allein deshalb nicht stimmen, da hier das Argument der Arcustangens–Funktion dimensionsbehaftet ist.
(4) Aus $z(t) = s(t) \cdot \gamma(t)$ folgt mit dem Faltungssatz:
$$Z(f) = S(f) \star \Gamma(f) = {1}/{2}
\cdot S(f) \star \delta (f) + S(f) \star \frac{1}{{\rm j} \cdot
2\pi f}\hspace{0.05cm}.$$
Da $S(f)$ reell ist, ergibt sich der Realteil von $Z(f)$ als der erste Term dieser Gleichung: $${\rm Re}[ Z(f)] = {1}/{2} \cdot S(f) \star \delta (f) = {1}/{2} \cdot S(f) \hspace{0.05cm}.$$
Der Realteil von $Z(f)$ hat somit die gleiche Rechteckform wie $S(f)$, ist aber nur halb so hoch: $${\rm Re}\{ Z(f)\}= \left\{ \begin{array}{c} T/2 \\ 0 \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array} \begin{array}{*{20}c} { |f|< 1/(2T)\hspace{0.05cm},} \\ { |f|> 1/(2T)\hspace{0.05cm},} \end{array} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm Vorschlag \hspace{0.15cm} 1}}.$$
(5) Mit dem Ergebnis der letzten Teilaufgabe folgt für den Imaginärteil: $${\rm Im}\{ Z(f)\} = S(f) \star \frac{(-1)}{{\rm j} \cdot 2\pi f} \hspace{0.05cm}.$$
Für hinreichend große Frequenzen $f \ge 1/(2T)$ liefert dieses Faltungsintegral: $${\rm Im}\{ Z(f)\} = -T \cdot \int_{f- 1/(2T)}^{ f+ 1/(2T)} { \frac{1}{2\pi x}}\hspace{0.1cm}{\rm d}x = \frac{T}{2\pi } \cdot {\rm ln}\hspace{0.15cm}\left |\frac{f- 1/(2T)}{f+ 1/(2T)}\right | \hspace{0.05cm} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm Vorschlag \hspace{0.15cm} 2}}.$$