Aufgaben:Exercise 2.3Z: DSB-AM due to Nonlinearity

• Return to book

ZSB–AM durch Nichtlinearität

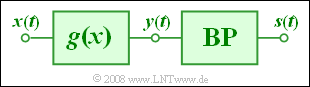
In dieser Aufgabe betrachten wir die Realisierung einer Zweiseitenband–Amplitudenmodulation mittels der nichtlinearen Kennlinie

$$y = g(x) = c_1 \cdot x + c_2 \cdot x^2+ c_3 \cdot x^3\hspace{0.05cm}$$

$$ \Rightarrow c_1 = 2,\hspace{0.2cm}c_2 = 0.25/{\rm V},\hspace{0.2cm}c_3 = 0 \hspace{0.1cm}{\rm bzw.}\hspace{0.1cm}c_3 = 0.01/{\rm V^2}\hspace{0.05cm}.$$

Am Eingang dieser Kennlinie liegt die Summe aus Trägersignal und Quellensignal an:

$$ x(t) = z(t) + q(t) = A_{\rm T} \cdot \cos(\omega_{\rm T} t)+ q(t),\hspace{0.2cm} A_{\rm T} = 4\,{\rm V}\hspace{0.05cm}.$$

Über das Quellensignal $q(t)$ ist bekannt, dass es Spektralanteile zwischen $1 \ \rm kHz$ und $9 \ \rm kHz$ (einschließlich dieser Grenzen) beinhaltet. Ab der Teilaufgabe (5) soll folgendes Quellensignal vorausgesetzt werden:

$$q(t) = A_{\rm 1} \cdot \cos(\omega_{\rm 1} t)+A_{\rm 9} \cdot \cos(\omega_{\rm 9} t) \hspace{0.05cm}.$$

Die Kreisfrequenzen seien $ω_1 = 2 π · 1 \ \rm kHz$ und $ω_9 = 2 π · 9\ \rm kHz$. Die dazugehörigen Amplituden sind wie folgt gegeben: $A_1 = 1\ \rm V$ und $A_9 = 2\ \rm V$.

In den Fragen zu dieser Aufgabe werden folgende Abkürzungen verwendet:

$$ y(t) = y_1(t) + y_2(t)+y_3(t),$$

$$y_1(t) = c_1 \cdot [z(t) + q(t)],$$

$$ y_2(t) = c_2 \cdot[z(t) + q(t)]^2,$$

$$y_3(t) = c_3 \cdot [z(t) + q(t)]^3 \hspace{0.05cm}.$$

Die Sendesignale $s(t)$ bzw. $s_1(t)$, $s_2(t)$ und $s_3(t)$ ergeben sich daraus jeweils durch Bandbegrenzung auf den Bereich von $90 \ \rm kHz$ bis $110 \ \rm kHz$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Zweiseitenband-Amplitudenmodulation.
• Bezug genommen wird insbesondere auf die Seite Amplitudenmodulation durch quadratische Kennlinie.

• Gegeben sind folgende trigonometrischen Umformungen:

$$ \cos^2(\alpha) = {1}/{2} \cdot \left[ 1 + \cos(2\alpha)\right] \hspace{0.05cm}, \hspace{0.5cm} \cos^3(\alpha) = {1}/{4} \cdot \left[ 3 \cdot \cos(\alpha) + \cos(3\alpha)\right] \hspace{0.05cm}.$$

Fragebogen

1

Wie sollte die Trägerfrequenz sinnvollerweise gewählt werden?

$f_{\rm T} \ = \ $ $\ \text{kHz}$

2

Welche Signalanteile beinhaltet $s_1(t)$?

	den Term $c_1 \cdot z(t)$,
	den Term $c_1 \cdot q(t)$.

3

Welche Signalanteile beinhaltet $s_2(t)$?

	den Term $c_2 · z^2(t)$,
	den Term $c_2 · q^2(t)$,
	den Term $2c_2 · z(t) · q(t)$.

4

Welche Signalanteile beinhaltet $s_3(t)$ zumindest teilweise?

	den Term $c_3 · z^3(t)$,
	den Term $3 · c_3 · z^2(t) · q(t)$,
	den Term $3 · c_3 · z(t) · q^2(t)$,
	den Term $c_3 · q^3(t)$.

5

Berechnen Sie $s(t)$, wenn $c_3 = 0$ gilt und sich das Quellensignal $q(t)$ aus zwei Cosinusschwingungen zusammensetzt.
Wie groß ist der Modulationsgrad $m$?

$m \ = \ $

6

Berechnen Sie nun das Sendesignal $s(t)$ unter der Voraussetzung $c_3 = \rm 0.01/V^{2}$. Welche der folgenden Aussagen treffen zu?

	Durch $c_3 ≠ 0$ wird die Spektrallinie bei $f_{\rm T}$ verändert.
	Durch $c_3 ≠ 0$ entstehen lineare, also kompensierbare Verzerrungen.
	Durch $c_3 ≠ 0$ entstehen nichtlineare, irreversible Verzerrungen.

Musterlösung

Solution

(1)  Die Trägerfrequenz ist sinnvollerweise gleich der Mittenfrequenz des Bandpasses: $f_{\rm T}\hspace{0.15cm}\underline{ = 100\ \rm kHz}$. Weicht $f_{\rm T}$ um nicht mehr als $±1 \ \rm kHz$ davon ab, ergibt sich ebenfalls eine „ZSB–AM”.

(2)  $s_1(t)$ beinhaltet nur den Träger $z(t)$   ⇒   Antwort 1. Das Quellensignal $q(t)$ wird durch den Bandpass entfernt.

(3)  Der quadratische Term $z^2(t)$ besteht aus einem Gleichanteil (bei $f = 0$) sowie einem Anteil bei $2f_{\rm T}$. Auch alle Spektralanteile von $q^2(t)$ liegen außerhalb des Bandpasses. Richtig ist somit die letzte Antwort.

(4)  Richtig sind die Lösungsvorschläge 1 und 3:

• Der Term $\cos^3(ω_Tt)$ hat seinen größten Signalanteil bei $f = f_{\rm T}$.
• Der dritte Lösungsvorschlag ($3 · c_3 · z(t) · q^2(t)$) liegt zwischen $100\ \rm kHz ± 18 \ \rm kHz $.
• Teile davon – nämlich die Frequenzanteile zwischen $90\ \rm kHz $ und $110 \ \rm kHz$ – werden durch den Bandpass nicht entfernt und sind somit auch in $s(t)$ enthalten.

(5)  Das Sendesignal besteht aus insgesamt fünf Frequenzen:

$$s(t) = c_1 \cdot A_{\rm T} \cdot \cos(\omega_{\rm T} t)+ c_2 \cdot A_{\rm T} \cdot A_{\rm 1} \cdot \cos((\omega_{\rm T} \pm \omega_{\rm 1})t) + c_2 \cdot A_{\rm T} \cdot A_{\rm 2} \cdot \cos((\omega_{\rm T} \pm \omega_{\rm 2})t) \hspace{0.05cm}.$$

Beachten Sie hierbei, dass der zweite und dritte Term jeweils zwei Signalfrequenzen (99 und 101 kHz bzw. 91 und 109 kHz) beinhaltet.

Spektrum des erzeugten AM–Signals

Mit $A_{\rm T} = 4 \ \rm V$, $A_1 = 1 V$, $A_9 = 2 \ \rm V$, $c_1 = 1$ und $c_2 = 1/A_{\rm T} = \rm 0.25/V$ gilt auch:

$$s(t) = 4\,{\rm V} \cdot \cos(\omega_{\rm T} t) + 1\,{\rm V} \cdot \cos((\omega_{\rm T} \pm \omega_{\rm 1})t) + 2\,{\rm V}\cdot \cos((\omega_{\rm T} \pm \omega_{\rm 2})t) \hspace{0.05cm}.$$

Daran erkennt man, dass für den Modulationsgrad gilt:

$$m =\frac{A_1 + A_9}{A_{\rm T}} = \rm \frac{1\ V + 2 \ V}{4 \ V} \hspace{0.15cm}\underline{=0.75}.$$

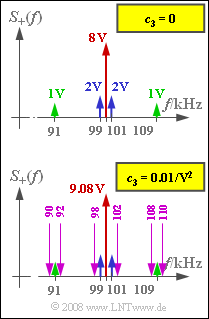
(6)  Die Grafik zeigt oben das Spektrum $S_+(f)$ – also nur positive Frequenzen – mit $c_3 = 0$.
Mit $c_3 ≠ 0$ fallen folgende zusätzliche Spektralanteile an:

$$c_3 \cdot z^3(t)= \frac{c_3 \cdot A_{\rm T}^3}{4} \cdot \left[ 3 \cdot \cos(\omega_{\rm T} t) + \cos(3\omega_{\rm T} t)\right] \hspace{0.05cm}.$$

• Der erste Anteil fällt in den Durchlassbereich des Bandpasses. Das Diracgewicht bei $f_{\rm T} =$ 100 kHz wird dadurch von ursprünglich $8 \ \rm V$ auf 8 V + 0.75 · 0.01/V² · 4³ V³ = $8.48 \ \rm V$ erhöht.
• Weiterhin liefert der dritte Spektralanteil von Teilaufgabe (4) einen unerwünschten Beitrag zu $S_+(f)$. Dabei gilt:

$$q^2(t) = \left[A_{\rm 1} \cdot \cos(\omega_{\rm 1} t)+A_{\rm 9} \cdot \cos(\omega_{\rm 9} t)\right]^2 = A_{\rm 1}^2 \cdot \cos^2(\omega_{\rm 1} t)+ A_{\rm 9}^2 \cdot \cos^2(\omega_{\rm 9}t) + 2 \cdot A_{\rm 1} \cdot A_{\rm 9} \cdot \cos(\omega_{\rm 1} t)\cdot \cos(\omega_{\rm 9} t)$$

$$ \Rightarrow \hspace{0.2cm} q^2(t) = \frac{A_{\rm 1}^2}{2} +\frac{A_{\rm 1}^2}{2} \cdot \cos(\omega_{\rm 2} t)+ \frac{A_{\rm 9}^2}{2} + \frac{A_{\rm 9}^2}{2} \cdot \cos(\omega_{\rm 18} t) + A_{\rm 1} \cdot A_{\rm 9} \cdot \cos(\omega_{\rm 8} t)+ A_{\rm 1} \cdot A_{\rm 9} \cdot \cos(\omega_{\rm 10} t).$$

Nach der Multiplikation mit $z(t)$ fallen alle diese Beiträge bis auf den vierten in den Bereich von 90 kHz bis 110 kHz. Das Gewicht bei $f_{\rm T} = 100\ \rm kHz$ wird um $3 · c_3 · A_{\rm T} · 0.5 (A_1^2 + A_9^2) = 0.6\ \rm V$ weiter erhöht und ist somit $9.08 \ \rm V$. Weitere Anteile ergeben sich bei:

• $98 \ \rm kHz$ und $102 \ \rm kHz$ mit den Gewichten $c_3 · A_{\rm T}/2 · A_1^2/2 = 0.03\ \rm V$,
• $92 \ \rm kHz$ und $108 \ \rm kHz$ mit den Gewichten $3c_3 · A_{\rm T}/2 · A_1 · A_9 = 0.12\ \rm V$,
• $90 \ \rm kHz$ und $110 \ \rm kHz$ mit den Gewichten $3c_3 · A_{\rm T}/2 · A_1 · A_9 = 0.12\ \rm V$.

Die untere Grafik zeigt das Spektrum $S_+(f)$ unter Berücksichtigung der kubischen Anteile. Man erkennt, dass neue Frequenzen entstanden sind, was auf nichtlineare Verzerrungen hindeutet. Richtig sind somit die Lösungsvorschläge 1 und 3.