Aufgaben:Exercise 3.11: Viterbi Path Finding

• Return to book

Ausgewertetes Trellisdiagramm

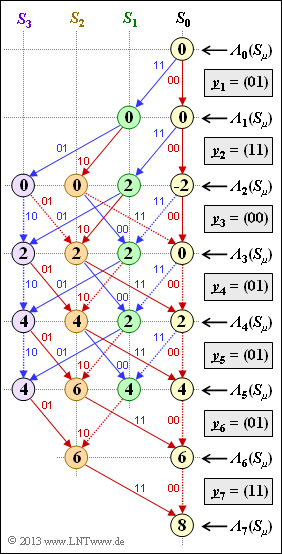
Ein Ergebnis von Aufgabe 3.10 war nebenstehende Trellis–Auswertung hinsichtlich der Metriken ${\it \Lambda}_i(S_{\mu})$. Zu allen Decodierschritten $i$ wurden die (im Allgemeinen) $2^m = 4$ Metriken bestimmt, wobei für jeden Knoten der größere von zwei Vergleichswerten ausgewählt wurde. Der Zweig mit dem niedrigeren Wert wurde verworfen. Man erkennt diese Zweige an punktierten Linien.

Ansonsten gelten die gleichen Voraussetzungen wie für die Aufgabe 3.10. Zum Beispiel kennzeichnet auch in nebenstehender Grafik ein roter Pfeil das Informationsbit $u_i = 0$ und ein blauer Pfeil steht für $u_i = 1$.

In der vorliegenden Aufgabe betrachten wir den zweiten und wichtigen Teil des Viterbi–Algorithmuses, nämlich die Suche nach den überlebenden Pfaden ${\it \Phi}_i(S_{\mu})$. Diese befinden sich zum Zeitpunkt $i$ im Zustand $S_{\mu}$. Die Suche organisiert man am besten in Rückwärtsrichtung (also in der Grafik von unten nach oben).

Zum Endzeitpunkt (im Beispiel $i = 7$) gibt es aufgrund der Terminierung nur einen überlebenden Pfad ${\it \Phi}_7(S_0)$. Aus diesem lässt sich extrahieren:

• die vom Decodierer ausgewählte Codesequenz $\underline{z}$   ⇒   größtmögliche Wahrscheinlichkeit ${\rm Pr}(\underline{z} = \underline{x})$,
• die dazugehörige Informationssequenz $\underline{v}$ mit der größtmöglichen Wahrscheinlichkeit ${\rm Pr}(\underline{v} = \underline{u})$.

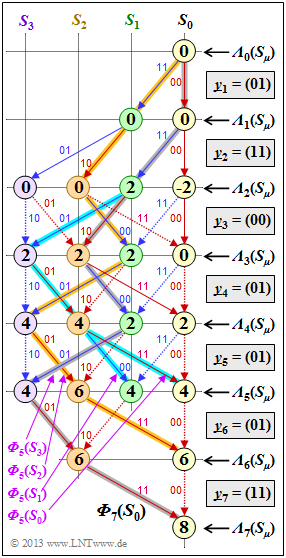
Eine Entscheidung zu einem früheren Zeitpunkt, zum Beispiel bei $i = 5$, erfüllt nicht immer das Maximum–Likelihood–Kriterium. Hier gibt es vier überlebende Pfade ${\it \Phi}_5(S_0), \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ {\it \Phi}_5(S_3)$, die zur Zeit $i = 5$ in den Zuständen $S_0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ S_3$ enden.

• Einer dieser vier Pfade ist mit Sicherheit Teil des Maximum–Likelihood–Pfades, der für $i → ∞$ (bei Terminierung deutlich früher, hier bei $i = 7$) der bestmögliche Pfad ist.
• Soll aber schon zum Zeitpunkt $i = 5$ ein Zwangsentscheid getroffen werden, so entscheidet man sich meist für den Pfad ${\it \Phi}_5(S_{\mu})$ mit der größten Metrik ${\it \Lambda}_5(S_{\mu})$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Decodierung von Faltungscodes.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Für welche Codesequenz $\underline{z}$ fällt die Entscheidung zum Zeitpunkt $i = 7$?

	$\underline{z} = (11, \, 10, \, 00, \, 01, \, 01, \, 11, \, 00)$,
	$\underline{z} = (00, \, 11, \, 10, \, 00, \, 01, \, 01, \, 11)$,
	$\underline{z} = (00, \, 11, \, 01, \, 01, \, 00, \, 10, \, 11)$.

2

Wieviele Übertragungsfehler sind (mindestens) aufgetreten?

$N_{\rm Bitfehler} \ = \ $

3

Für welche Informationssequenz $\underline{\upsilon}$ entscheidet sich der Viterbi–Decoder?

	$\underline{v} = (0, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0)$,
	$\underline{v} = (1, \, 0, \, 1, \, 1, \, 0, \, 0, \, 0)$,
	$\underline{v} = (0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0)$.

4

Wäre bereits bei $i = 6$ eine endgültige Entscheidung möglich gewesen?

	Ja.
	Nein.

5

Welche überlebenden Pfade gibt es zum Zeitpunkt $i = 5$?

	$S_0 → S_0 → S_1 → S_3 → S_2 → S_0$,
	$S_0 → S_0 → S_1 → S_3 → S_2 → S_1$,
	$S_0 → S_1 → S_2 → S_1 → S_3 → S_2$,
	$S_0 → S_0 → S_1 → S_2 → S_1 → S_3$.

6

Für welchen Pfad würde man sich zum Zeitpunkt $i = 5$ entscheiden?

	$S_0 → S_0 → S_1 → S_3 → S_2 → S_0$,
	$S_0 → S_0 → S_1 → S_3 → S_2 → S_1$,
	$S_0 → S_1 → S_2 → S_1 → S_3 → S_2$,
	$S_0 → S_0 → S_1 → S_2 → S_1 → S_3$.

7

Welcher der Pfade wäre aber wahrscheinlich der richtige?

	$S_0 → S_0 → S_1 → S_3 → S_2 → S_0$,
	$S_0 → S_0 → S_1 → S_3 → S_2 → S_1$,
	$S_0 → S_1 → S_2 → S_1 → S_3 → S_2$,
	$S_0 → S_0 → S_1 → S_2 → S_1 → S_3$.

Musterlösung

Solution

(1)  Eindeutig findet man den überlebenden Pfad durch Rückwärtssuche, also vom Knoten ${\it \Lambda}_7(S_0)$ zum Knoten ${\it \Lambda}_0(S_0)$. Anhand der an den Übergängen angegebenen Codesequenz $(00, \, 01, \, 10$ oder $11)$ erhält man somit in Vorwärtsrichtung das Ergebnis gemäß Lösungsvorschlag 2  ⇒  ${\it \Phi}_7(S_0)$ in Grafik:

$$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$

Entlang der anderen Pfade gelangt man nicht bis zum Endknoten ${\it \Lambda}_7(S_0)$.

(2)  Durch Vergleich der in der Teilaufgabe (1) ausgewählten Codesequenz $\underline{z}$ mit der Empfangssequenz

$$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big )$$

erkennt man drei Bitfehler an den Positionen 2, 5 und 8. Wurde eine Codesequenz $\underline{x} ≠ \underline{z}$ gesendet, so können es natürlich mehr sein. Aufgrund des Endwertes ${\it \Lambda}_7(S_0) = 8$ bzw. ${\it \Gamma}_7(S_0) = 3$ – siehe Aufgabe A3.10 – kann man aber davon ausgehen, dass eine richtige Entscheidung  ⇒  $\underline{z} = \underline{x}$ getroffen wurde.

(3) 

Zur Viterbi–Pfadsuche

Anhand der Farben des überlebenden Pfades – rot steht für $u_i = 0$ und blau für $u_i = 1$ – erkennt man die Richtigkeit von Lösungsvorschlag 1: rot – blau – rot – blau – blau – rot – rot. Es ist anzumerken, dass die eigentliche Informationssequenz $\underline{u}$ nur die Länge $L = 5$ aufweist. Erst durch die Terminierung kommt man zur Gesamtlänge $L' = L + m = 7$.

(4)  Zur Zeit $i = 6$ gibt es noch zwei überlebende Pfade. Eine Entscheidung könnte man zwangsweise anhand der größeren Metrik treffen. Wegen ${\it \Lambda}_6(S_0) = {\it \Lambda}_6(S_2) = 6$ ist dies aber in unserem Beispiel nicht möglich  ⇒  Nein.

(5)  Die Grafik zeigt, dass alle Lösungsvorschläge richtig sind. Die Pfade sind mit ${\it \Phi}_5(S_0), \ ... \ , \ {\it \Phi}_5(S_3)$ bezeichnet.

(6)  Die Zwangsentscheidung zum Zeitpunkt $i = 5$ würde den Pfad mit der größten Metrik ${\it \Lambda}_5(S_{\mu})$ auswählen, also den Pfad ${\it \Phi}_5(S_2)$ entsprechend Lösungsvorschlag 3.

(7)  Aufgrund unserer Lösung zur Teilaufgabe (1) wäre der Pfad ${\it \Phi}_5(S_3)$ gemäß Lösungsvorschlag 4 die bessere Wahl gewesen. Dieser ist Teil des Pfades ${\it \Phi}_7(S_0)$. Zum Zeitpunkt $i = 5$ spricht aber noch nichts für diese Wahl. Der (letztlich richtige) Pfad wird erst durch die beiden Terminierungsbit herausgehoben.