Difference between revisions of "Aufgaben:Exercise 3.6: State Transition Diagram"
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm}} | {{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm}} | ||
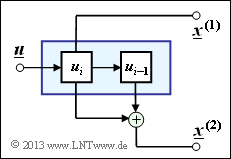
| − | [[File:P_ID2648__KC_A_3_6.png|right|frame| | + | [[File:P_ID2648__KC_A_3_6.png|right|frame|Eine einfache Reqalisierung eines Rate–1/2–Faltungscodierers]] |
| − | Eine Beschreibungsmöglichkeit für Faltungscodierer bietet das so genannte <i>Zustandsübergangsdiagramm</i> | + | Eine Beschreibungsmöglichkeit für Faltungscodierer bietet das so genannte <i>Zustandsübergangsdiagramm</i>. Beinhaltet der Coder $m$ Speicherregister ⇒ Einflusslänge $\nu = m + 1$, so gibt es nach der aktuellen Speicherbelegung verschiedene Zustände $S_{\mu}$ mit $0 ≤ \mu ≤ 2^m \, –1$, wobei für den Index gilt: |
:$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} | :$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Diese Art der Coderbeschreibung soll auf den oben skizzierten Faltungscodierer der Rate $R = 1/2$ angewendet werden. | Diese Art der Coderbeschreibung soll auf den oben skizzierten Faltungscodierer der Rate $R = 1/2$ angewendet werden. | ||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
* Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm| Codebeschreibung mit Zustands– und Trellisdiagramm]]. | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm| Codebeschreibung mit Zustands– und Trellisdiagramm]]. | ||
| + | *Bezug genommen wird insbesondere auf den Abschnitt [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister|Zustandsdefinition für ein Speicherregister]]. | ||
* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Line 18: | Line 23: | ||
{Wieviele Zustände weist dieser Faltungscodierer auf? | {Wieviele Zustände weist dieser Faltungscodierer auf? | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Anzahl \ der \ Zustände} \ = \ ${ 2 | + | ${\rm Anzahl \ der \ Zustände} \ = \ ${ 2 } |
{Kommt man von jedem Zustand zu allen anderen Zuständen? | {Kommt man von jedem Zustand zu allen anderen Zuständen? | ||
| Line 41: | Line 46: | ||
{Welche Informationssequenzen sind möglich? | {Welche Informationssequenzen sind möglich? | ||
|type="[]"} | |type="[]"} | ||
| − | + $\underline{u} = (1, \, 1, \, 0, \, 0, \, 1 \, 1, \, ...)$, | + | + $\underline{u} = (1, \, 1, \, 0, \, 0, \, 1 \, 1, \, \text{...}\hspace{0.05cm})$, |
| − | + $\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \, ...)$. | + | + $\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \, \text{...}\hspace{0.05cm})$. |
{Welche Codesequenzen sind möglich? | {Welche Codesequenzen sind möglich? | ||
|type="[]"} | |type="[]"} | ||
| − | + $\underline{x} = (11, \, 10, \, 01, \, 00, \, 11, \, 10, \, ...)$, | + | + $\underline{x} = (11, \, 10, \, 01, \, 00, \, 11, \, 10, \, \text{...}\hspace{0.05cm})$, |
| − | - $\underline{x} = (11, \, 00, \, 10, \, 01, \, 11, \, 00, \, ...)$. | + | - $\underline{x} = (11, \, 00, \, 10, \, 01, \, 11, \, 00, \, \text{...}\hspace{0.05cm})$. |
</quiz> | </quiz> | ||
Revision as of 10:17, 22 January 2018
Eine Beschreibungsmöglichkeit für Faltungscodierer bietet das so genannte Zustandsübergangsdiagramm. Beinhaltet der Coder $m$ Speicherregister ⇒ Einflusslänge $\nu = m + 1$, so gibt es nach der aktuellen Speicherbelegung verschiedene Zustände $S_{\mu}$ mit $0 ≤ \mu ≤ 2^m \, –1$, wobei für den Index gilt:
- $$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$
Diese Art der Coderbeschreibung soll auf den oben skizzierten Faltungscodierer der Rate $R = 1/2$ angewendet werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm.
- Bezug genommen wird insbesondere auf den Abschnitt Zustandsdefinition für ein Speicherregister.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- den Zustand $S_0 \ \Rightarrow \ u_{i–1} = 0$,
- den Zustand $S_1 \ \Rightarrow \ u_{i–1} = 1$.
(2) Von jedem Zustand gehen $2^k = 2$ Pfeile zu verschiedenene Zuständen ab. Da es nur zwei Zustände gibt, ist die Antwort JA richtig.
(3) Das zum Zeitpunkt $i$ anliegende Informationsbit $u_i$ ist hinsichtlich des darauf folgenden Zeitpunkts $(j = i + 1)$ das vorherige Bit $(u_{j–1})$. Damit gilt $s_{i+1} = u_i$. Nur mit $u_i = 0$ kommt man von $s_i = S_1$ nach $s_{i+1} = S_0$ ⇒ Lösungsvorschlag 1.
Aus $s_i = S_1$ ⇒ $u_{i–1} = 1$ folgt weiter:
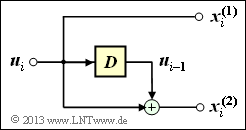
- $${x}_i^{(1)} = u_i = 0\hspace{0.05cm},\hspace{0.2cm}{x}_i^{(2)} = u_i + u_{i-1}= 0+1 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\underline{x}_i = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \hspace{0.05cm}. $$
Richtig ist also zusätzlich noch der Lösungsvorschlag 3. Den Lösungsvorschlag 4 hätte man von Anfang an ausschließen können. Die Grafik auf dem Angabenblatt zeigt eindeutig, dass der Coder systematisch ist: $x_i^{(1)} = u_i$. Die Kombination $u_i = 0$ und $\underline{x}_i = (1, 0)$ würde dem widersprechen.
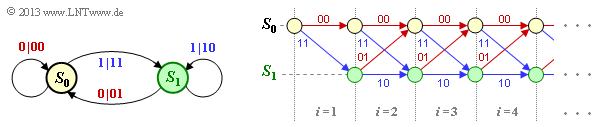
(4) Auf ähnlichem Lösungsweg wie in der Teilaufgabe (3) gelangt man zum Ergebnis, dass hier die Lösungsvorschläge 2 und 4 zutreffen. Damit ergeben sich das folgende Zustandsübergangsdiagramm (links) und das daraus ableitbare Trellisdiagramm:
Rote Pfeile kennzeichnen das Informationsbit $u_i = 0$, während bei blauen Pfeilen $u_i = 1$ anzusetzen ist.
(5) Beide Lösungsvorschläge sind richtig. Für die Informationssequenzen gibt es (außer binär) keine weiteren Beschränkungen.
(6) Richtig ist der Lösungsvorschlag 1. Ausgehend vom Zustand $S_0$ kommt man
- mit $u_1 = 1$ zum Zustand $S_1$, Ausgabe $11$,
- mit $u_2 = 1$ zum Zustand $S_1$, Ausgabe $10$,
- mit $u_3 = 0$ zum Zustand $S_0$, Ausgabe $01$,
- mit $u_4 = 0$ zum Zustand $S_0$, Ausgabe $00$,
- mit $u_5 = 1$ zum Zustand $S_1$, Ausgabe $11$,
- mit $u_6 = 1$ zum Zustand $S_1$, Ausgabe $10$.
Dagegen ist die zweite Codesequenz nicht möglich:
- Die Ausgabe „$11$” bedeutet, dass man bei $S_0$ gestartet ist und mit $u_1 = 1$ zum Zustand $S_1$ kommt.
- Im Zustand $S_1$ sind dann aber nur die Ausgaben „$01$” und „$10$” möglich, nicht jedoch „$00$”.