Difference between revisions of "Aufgaben:Exercise 2.15Z: Block Error Probability once more"
m (Textersetzung - „* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „“) |
|||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Fehlerwahrscheinlichkeit und Anwendungsgebiete}} | {{quiz-Header|Buchseite=Kanalcodierung/Fehlerwahrscheinlichkeit und Anwendungsgebiete}} | ||
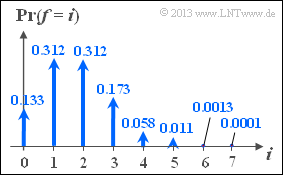
| − | [[File:P_ID2574__KC_Z_2_15.png|right|frame|Wahrscheinlichkeiten | + | [[File:P_ID2574__KC_Z_2_15.png|right|frame|Binominal–Wahrscheinlichkeiten]] |
| − | Bei Verwendung eines Reed–Solomon–Codes mit der Korrekturfähigkeit $t$ und [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete#Blockfehlerwahrscheinlichkeit_f.C3.BCr_RSC_und_BDD|Bounded Distance Decoding]] (BDD) erhält man mit | + | Bei Verwendung eines Reed–Solomon–Codes mit der Korrekturfähigkeit $t$ und [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete#Blockfehlerwahrscheinlichkeit_f.C3.BCr_RSC_und_BDD|Bounded Distance Decoding]] (BDD) erhält man mit |
| − | * der Codewortlänge $n$ und | + | * der Codewortlänge $n$ und |
| − | * der Symbolverfälschungswahrscheinlichkeit $\ | + | * der Symbolverfälschungswahrscheinlichkeit $\varepsilon_{\rm S}$ |
| Line 11: | Line 11: | ||
\sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$ | \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$ | ||
| − | In dieser Aufgabe soll die Blockfehlerwahrscheinlichkeit für den $\rm RSC \, (7, \, 3, \, 5)_8$ und verschiedene $\ | + | In dieser Aufgabe soll die Blockfehlerwahrscheinlichkeit für den $\rm RSC \, (7, \, 3, \, 5)_8$ und verschiedene $\varepsilon_{\rm S}$–Werte berechnet und angenähert werden. |
| + | |||
| + | Obige Gleichung erinnert an die [[Stochastische_Signaltheorie/Binomialverteilung|Biomialverteilung]]. Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung für die Parameter $n = 7$ (Codewortlänge) und $\varepsilon_{\rm S} = 0.25$ (Symbolverfälschungswahrscheinlichkeit). | ||
| + | |||
| + | |||
| + | |||
| Line 18: | Line 23: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete| Fehlerwahrscheinlichkeit und Anwendungsgebiete]]. | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete| Fehlerwahrscheinlichkeit und Anwendungsgebiete]]. |
| − | * Zur Kontrolle können Sie das interaktive Applet [[Applets: | + | * Zur Kontrolle können Sie das interaktive Applet [[Applets:Binomial-_und_Poissonverteilung_(Applet)|Binomial- und Poissonverteilung]] benutzen. |
| Line 27: | Line 32: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Blockfehlerwahrscheinlichkeit ergibt sich für $\varepsilon_{\rm S} = 10^{-1}$? | + | {Welche Blockfehlerwahrscheinlichkeit ergibt sich für $\varepsilon_{\rm S} = 10^{-1}$? |
|type="{}"} | |type="{}"} | ||
$\rm Pr(Blockfehler) \ = \ ${ 2.57 3% } $\ \cdot 10^{-2}$ | $\rm Pr(Blockfehler) \ = \ ${ 2.57 3% } $\ \cdot 10^{-2}$ | ||
| − | {Welche Blockfehlerwahrscheinlichkeit ergibt sich für $\varepsilon_{\rm S} =10^{-2}$? | + | {Welche Blockfehlerwahrscheinlichkeit ergibt sich für $\varepsilon_{\rm S} =10^{-2}$? |
|type="{}"} | |type="{}"} | ||
$\rm Pr(Blockfehler) \ = \ ${ 3.396 3% } $\ \cdot 10^{-5}$ | $\rm Pr(Blockfehler) \ = \ ${ 3.396 3% } $\ \cdot 10^{-5}$ | ||
| − | {Welches Ergebnis erhält man für $\varepsilon_{\rm S} =10^{-2}$, wenn man nur den Term $f = t + 1$ berücksichtigt? | + | {Welches Ergebnis erhält man für $\varepsilon_{\rm S} =10^{-2}$, wenn man nur den Term $f = t + 1$ berücksichtigt? |
|type="{}"} | |type="{}"} | ||
$\rm Näherung \text{:} \hspace{0.2cm} Pr(Blockfehler) \ \approx \ ${ 3.362 3% } $\ \cdot 10^{-5}$ | $\rm Näherung \text{:} \hspace{0.2cm} Pr(Blockfehler) \ \approx \ ${ 3.362 3% } $\ \cdot 10^{-5}$ | ||
| − | {Welches Ergebnis erhält man näherungsweise für $\varepsilon_{\rm S} = 10^{-3}$? | + | {Welches Ergebnis erhält man näherungsweise für $\varepsilon_{\rm S} = 10^{-3}$? |
|type="{}"} | |type="{}"} | ||
| − | $\rm Pr(Blockfehler) \ | + | $\rm Pr(Blockfehler) \ \approx \ ${ 3.49 3% } $\ \cdot 10^{-8}$ |
| − | {Welches $\varepsilon_{\rm S}$ benötigt man für die Blockfehlerwahrscheinlichkeit $10^{-10}$? | + | {Welches $\varepsilon_{\rm S}$ benötigt man für die Blockfehlerwahrscheinlichkeit $10^{-10}$? |
|type="{}"} | |type="{}"} | ||
$\varepsilon_{\rm S} \ = \ ${ 1.42 3% } $\ \cdot 10^{-4}$ | $\varepsilon_{\rm S} \ = \ ${ 1.42 3% } $\ \cdot 10^{-4}$ | ||
Revision as of 17:06, 30 May 2019
Bei Verwendung eines Reed–Solomon–Codes mit der Korrekturfähigkeit $t$ und Bounded Distance Decoding (BDD) erhält man mit
- der Codewortlänge $n$ und
- der Symbolverfälschungswahrscheinlichkeit $\varepsilon_{\rm S}$
für die Blockfehlerwahrscheinlichkeit:
- $${\rm Pr(Blockfehler)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$
In dieser Aufgabe soll die Blockfehlerwahrscheinlichkeit für den $\rm RSC \, (7, \, 3, \, 5)_8$ und verschiedene $\varepsilon_{\rm S}$–Werte berechnet und angenähert werden.
Obige Gleichung erinnert an die Biomialverteilung. Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung für die Parameter $n = 7$ (Codewortlänge) und $\varepsilon_{\rm S} = 0.25$ (Symbolverfälschungswahrscheinlichkeit).
Hinweise:
- Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit und Anwendungsgebiete.
- Zur Kontrolle können Sie das interaktive Applet Binomial- und Poissonverteilung benutzen.
Fragebogen
Musterlösung
- $${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{f = 3}^{7} {7 \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{7-f} $$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr(Blockfehler)} ={7 \choose 3} \cdot 0.1^3 \cdot 0.9^4 + {7 \choose 4} \cdot 0.1^4 \cdot 0.9^3 + {7 \choose 5} \cdot 0.1^5 \cdot 0.9^2+ {7 \choose 6} \cdot 0.1^6 \cdot 0.9+ {7 \choose 7} \cdot 0.1^7 \hspace{0.05cm}.$$
Nach dieser Berechnung müssten fünf Terme berücksichtigt werden. Da aber auch
- $${\rm Pr(Blockfehler)} = \sum_{f = 0}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} = 1$$
gilt, kommt man über den nachfolgenden Rechenweg schneller zum Erfolg:
- $${\rm Pr(Blockfehler)} =1 - \big [ {7 \choose 0} \cdot 0.9^7 + {7 \choose 1} \cdot 0.1 \cdot 0.9^6 + {7 \choose 2} \cdot 0.1^2 \cdot 0.9^5 \big ] =1 - \big [ 0.4783 + 0.3720 + 0.1240 \big ] \hspace{0.15cm} \underline{= 2.57 \cdot 10^{-2}} \hspace{0.05cm}.$$
(2) Analog zur Teilaufgabe (1) erhält man hier:
- $${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - \big [ 0.99^7 + 7 \cdot 0.01 \cdot 0.99^6 + 21 \cdot 0.01^2 \cdot 0.99^5 \big ] =1 - \big [ 0.9321 + 0.0659 + 0.0020 \big ] \approx 0 \hspace{0.05cm}.$$
Das bedeutet: Für die Wahrscheinlichkeit $\varepsilon_{\rm S} = 0.01$ ist die vereinfachte Rechnung sehr fehleranfällig, weil sich für den Klammerausdruck ein Wert nahezu $1$ ergibt. Die vollständige Rechnung ergibt hier:
- $${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 3} \cdot 0.01^3 \cdot 0.99^4 + {7 \choose 4} \cdot 0.01^4 \cdot 0.99^3 + {7 \choose 5} \cdot 0.01^5 \cdot 0.99^2+ {7 \choose 6} \cdot 0.01^6 \cdot 0.99+ {7 \choose 7} \cdot 0.01^7 $$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr(Blockfehler)}= 10^{-6} \cdot \big [ 33.6209 + 0.3396 + 0.0021 + ... \big ] \hspace{0.15cm} \underline{ \approx 3.396 \cdot 10^{-5}} \hspace{0.05cm}.$$
(3) Aus der Musterlösung zur Teilaufgabe (2) kann das Ergebnis direkt abgelesen werden:
- $${\rm Pr(Blockfehler)} \hspace{0.15cm} \underline{ \approx 3.362 \cdot 10^{-5}} \hspace{0.05cm}.$$
- Der relative Fehler beträgt ca. $-1\%$.
- Das Minuszeichen zeigt an, dass es sich hier nur um eine Näherung handelt und nicht um eine Schranke: Der Näherungswert ist etwas kleiner als der tatsächliche Wert.
(4) Beschränkt man sich auf den relevanten Term $(f = 3)$, so ergibt sich für $\varepsilon_{\rm S} = 0.001$:
- $${\rm Pr(Blockfehler)} \approx {7 \choose 3} \cdot [10^{-3}]^3 \cdot 0.999^4 \hspace{0.15cm} \underline{ \approx 3.49 \cdot 10^{-8}} \hspace{0.05cm}.$$
Der relative Fehler beträgt hier nur noch etwa $-0.1\%$.
(5) Entsprechend der hergeleiteten Näherung gilt für den betrachteten Code:
- $${\rm Pr(Blockfehler)} \approx {7 \choose 3} \cdot {\varepsilon_{\rm S}}^3 = 35 \cdot {\varepsilon_{\rm S}}^3\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr(Blockfehler)} = 10^{-10}: \hspace{0.4cm} {\varepsilon_{\rm S}} = \big ( \frac{10^{-10}}{35} \big )^{1/3} = 2.857^{1/3} \cdot 10^{-4} \hspace{0.15cm} \underline{ \approx 1.42 \cdot 10^{-4}}\hspace{0.05cm}.$$