Difference between revisions of "Aufgaben:Exercise 3.10: Metric Calculation"
m (Textersetzung - „* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 2: | Line 2: | ||
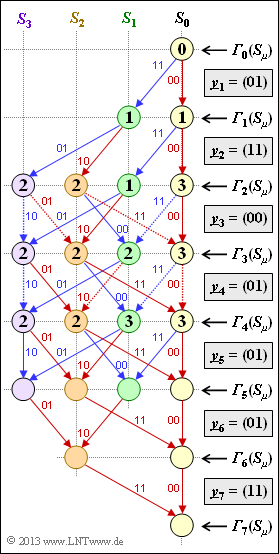
[[File:P_ID2681__KC_A_3_10.png|right|frame|Nur teilweise ausgewertetes Trellis]] | [[File:P_ID2681__KC_A_3_10.png|right|frame|Nur teilweise ausgewertetes Trellis]] | ||
| − | Im [[Kanalcodierung/Decodierung_von_Faltungscodes#Vorbemerkungen_zu_den_nachfolgenden_Decodierbeispielen| Theorieteil]] zu diesem Kapitel wurde die Berechnung der Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ ausführlich behandelt, die auf der Hamming–Distanz $d_{\rm H}(\underline{x}', \ \underline{y}_i)$ zwischen den möglichen Codeworten $\underline{x}' ∈ \{00, \, 01, \, 10, \, 11\}$ und | + | Im [[Kanalcodierung/Decodierung_von_Faltungscodes#Vorbemerkungen_zu_den_nachfolgenden_Decodierbeispielen| Theorieteil]] zu diesem Kapitel wurde die Berechnung der Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ ausführlich behandelt, die auf der Hamming–Distanz $d_{\rm H}(\underline{x}\hspace{0.05cm}', \ \underline{y}_i)$ zwischen den möglichen Codeworten $\underline{x}\hspace{0.05cm}' ∈ \{00, \, 01, \, 10, \, 11\}$ und dem zum Zeitpunkt $i$ empfangenen 2–Bit–Worten $\underline{y}_i$ basiert. |
Die Aufgabe beschäftigt sich genau mit dieser Thematik. In nebenstehender Grafik | Die Aufgabe beschäftigt sich genau mit dieser Thematik. In nebenstehender Grafik | ||
| − | * ist das betrachtete Trellis dargestellt – gültig für den Code mit Rate $R = 1/2$, Gedächtnis $m = 2$ sowie $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$, | + | * ist das betrachtete Trellis dargestellt – gültig für den Code mit Rate $R = 1/2$, Gedächtnis $m = 2$ sowie $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$, |
| − | * sind die Empfangsworte $\underline{y}_1 = (01), \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \underline{y}_7 = (11)$ in den Rechtecken angegeben, | + | * sind die Empfangsworte $\underline{y}_1 = (01), \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \underline{y}_7 = (11)$ in den Rechtecken angegeben, |
| − | * sind alle Fehlergrößen ${\it \Gamma}_0(S_{\mu}), \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ {\it \Gamma}_4(S_{\mu})$ | + | * sind alle Fehlergrößen ${\it \Gamma}_0(S_{\mu}), \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ {\it \Gamma}_4(S_{\mu})$ bereits eingetragen. |
| − | Beispielsweise ergibt sich die Fehlergröße ${\it \Gamma}_4(S_0)$ mit $\underline{y}_4 = (01)$ als das Minimum der beiden Vergleichswerte | + | Beispielsweise ergibt sich die Fehlergröße ${\it \Gamma}_4(S_0)$ mit $\underline{y}_4 = (01)$ als das Minimum der beiden Vergleichswerte |
* ${\it \Gamma}_3(S_0) + d_{\rm H}((00), \ (01)) = 3 + 1 = 4$, und | * ${\it \Gamma}_3(S_0) + d_{\rm H}((00), \ (01)) = 3 + 1 = 4$, und | ||
* ${\it \Gamma}_3(S_2) + d_{\rm H}((11), \ (01)) = 2 + 1 = 3$. | * ${\it \Gamma}_3(S_2) + d_{\rm H}((11), \ (01)) = 2 + 1 = 3$. | ||
| − | Der überlebende Zweig – hier von ${\it \Gamma}_3(S_2)$ nach ${\it \Gamma}_4(S_0)$ – ist durchgezogen gezeichnet, der eliminierte Zweig von ${\it \Gamma}_3(S_0)$ nach ${\it \Gamma}_4(S_0)$ punktiert. Rote Pfeile stehen für das Informationsbit $u_i = 0$, blaue Pfeile für $u_i = 1$. | + | Der überlebende Zweig – hier von ${\it \Gamma}_3(S_2)$ nach ${\it \Gamma}_4(S_0)$ – ist durchgezogen gezeichnet, der eliminierte Zweig von ${\it \Gamma}_3(S_0)$ nach ${\it \Gamma}_4(S_0)$ punktiert. Rote Pfeile stehen für das Informationsbit $u_i = 0$, blaue Pfeile für $u_i = 1$. |
| − | In der Teilaufgabe (4) soll der Zusammenhang zwischen | + | In der Teilaufgabe '''(4)''' soll der Zusammenhang zwischen |
| − | *der ${\it \Gamma}_i(S_{\mu})$–Minimierung und | + | *der ${\it \Gamma}_i(S_{\mu})$–Minimierung und |
| − | *der ${\it \Lambda}_i(S_{\mu})$–Maximierung | + | *der ${\it \Lambda}_i(S_{\mu})$–Maximierung |
| − | herausgearbeitet werden. Hierbei bezeichnet man die Knoten ${\it \Lambda}_i(S_{\mu})$ als <i>Metriken</i>, wobei sich der Metrikzuwachs gegenüber den Vorgängerknoten aus dem Korrelationswert $〈\underline{x}_i', \, \underline{y}_i 〉$ ergibt. Näheres zu dieser Thematik finden Sie auf den folgenden Theorieseiten: | + | herausgearbeitet werden. Hierbei bezeichnet man die Knoten ${\it \Lambda}_i(S_{\mu})$ als <i>Metriken</i>, wobei sich der Metrikzuwachs gegenüber den Vorgängerknoten aus dem Korrelationswert $〈\underline{x}_i\hspace{0.05cm}', \, \underline{y}_i 〉$ ergibt. Näheres zu dieser Thematik finden Sie auf den folgenden Theorieseiten: |
* [[Kanalcodierung/Decodierung_von_Faltungscodes#Zusammenhang_zwischen_Hamming.E2.80.93Distanz_und_Korrelation| Zusammenhang zwischen Hamming–Distanz und Korrelation]], | * [[Kanalcodierung/Decodierung_von_Faltungscodes#Zusammenhang_zwischen_Hamming.E2.80.93Distanz_und_Korrelation| Zusammenhang zwischen Hamming–Distanz und Korrelation]], | ||
* [[Kanalcodierung/Decodierung_von_Faltungscodes#Viterbi.E2.80.93Algorithmus.2C_basierend_auf_Korrelation_und_Metriken| Viterbi–Algorithmus, basierend auf Korrelation und Metriken]], | * [[Kanalcodierung/Decodierung_von_Faltungscodes#Viterbi.E2.80.93Algorithmus.2C_basierend_auf_Korrelation_und_Metriken| Viterbi–Algorithmus, basierend auf Korrelation und Metriken]], | ||
| − | * [[Kanalcodierung/Decodierung_von_Faltungscodes#Viterbi.E2.80.93Entscheidung_bei_nicht.E2.80.93terminierten_Faltungscodes| Viterbi–Entscheidung bei nicht– | + | * [[Kanalcodierung/Decodierung_von_Faltungscodes#Viterbi.E2.80.93Entscheidung_bei_nicht.E2.80.93terminierten_Faltungscodes| Viterbi–Entscheidung bei nicht–terminierten Faltungscodes]]. |
| + | |||
| + | |||
| Line 33: | Line 35: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Decodierung_von_Faltungscodes| Decodierung von Faltungscodes]]. | + | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Decodierung_von_Faltungscodes| Decodierung von Faltungscodes]]. |
| − | * Vorerst nicht betrachtet wird die Suche der überlebenden Pfade. Damit beschäftigt sich für das gleiche Beispiel die | + | * Vorerst nicht betrachtet wird die Suche der überlebenden Pfade. Damit beschäftigt sich für das gleiche Beispiel die spätere [[Aufgaben:3.11_Viterbi%E2%80%93Pfadsuche| Aufgabe 3.11]]. |
| Line 42: | Line 44: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lauten die Fehlergrößen für den Zeitpunkt $i = 5$? | + | {Wie lauten die Fehlergrößen für den Zeitpunkt $i = 5$? |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_5(S_0) \ = \ ${ 3 3% } | ${\it \Gamma}_5(S_0) \ = \ ${ 3 3% } | ||
| Line 49: | Line 51: | ||
${\it \Gamma}_5(S_3) \ = \ ${ 3 3% } | ${\it \Gamma}_5(S_3) \ = \ ${ 3 3% } | ||
| − | {Wie lauten die Fehlergrößen für den Zeitpunkt $i = 6$? | + | {Wie lauten die Fehlergrößen für den Zeitpunkt $i = 6$? |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_6(S_0) \ = \ ${ 3 3% } | ${\it \Gamma}_6(S_0) \ = \ ${ 3 3% } | ||
${\it \Gamma}_6(S_2) \ = \ ${ 3 3% } | ${\it \Gamma}_6(S_2) \ = \ ${ 3 3% } | ||
| − | {Welcher Endwert ergibt sich bei diesem Trellis, basierend auf ${\it \Gamma}_i(S_{\mu})$? | + | {Welcher Endwert ergibt sich bei diesem Trellis, basierend auf ${\it \Gamma}_i(S_{\mu})$? |
|type="[]"} | |type="[]"} | ||
| − | + Es gilt ${\it \Gamma}_7(S_0) = 3$. | + | + Es gilt ${\it \Gamma}_7(S_0) = 3$. |
- Dieser Endwert lässt auf eine fehlerfreie Übertragung schließen. | - Dieser Endwert lässt auf eine fehlerfreie Übertragung schließen. | ||
+ Dieser Endwert lässt auf drei Übertragungsfehler schließen. | + Dieser Endwert lässt auf drei Übertragungsfehler schließen. | ||
| − | {Welche Aussagen sind für die ${\it \Lambda}_i(S_{\mu})$–Auswertung zutreffend? | + | {Welche Aussagen sind für die ${\it \Lambda}_i(S_{\mu})$–Auswertung zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + Die Metriken ${\it \Lambda}_i(S_{\mu})$ liefern gleiche Informationen wie ${\it \Gamma}_i(S_{\mu})$. | + | + Die Metriken ${\it \Lambda}_i(S_{\mu})$ liefern gleiche Informationen wie ${\it \Gamma}_i(S_{\mu})$. |
| − | + Für alle Knoten gilt ${\it \Lambda}_i(S_{\mu}) = 2 \cdot [i \, –{\it \Gamma}_i(S_{\mu})$. | + | + Für alle Knoten gilt ${\it \Lambda}_i(S_{\mu}) = 2 \cdot \big [i \, –{\it \Gamma}_i(S_{\mu})\big ]$. |
| − | - Für die Metrikzuwächse gilt $〈 \underline{x}_i', \, \underline{y}_i 〉 ∈ \{0, \, 1, \, 2\}$. | + | - Für die Metrikzuwächse gilt $〈 \underline{x}_i', \, \underline{y}_i 〉 ∈ \{0, \, 1, \, 2\}$. |
</quiz> | </quiz> | ||
Revision as of 08:00, 26 June 2019
Im Theorieteil zu diesem Kapitel wurde die Berechnung der Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ ausführlich behandelt, die auf der Hamming–Distanz $d_{\rm H}(\underline{x}\hspace{0.05cm}', \ \underline{y}_i)$ zwischen den möglichen Codeworten $\underline{x}\hspace{0.05cm}' ∈ \{00, \, 01, \, 10, \, 11\}$ und dem zum Zeitpunkt $i$ empfangenen 2–Bit–Worten $\underline{y}_i$ basiert.
Die Aufgabe beschäftigt sich genau mit dieser Thematik. In nebenstehender Grafik
- ist das betrachtete Trellis dargestellt – gültig für den Code mit Rate $R = 1/2$, Gedächtnis $m = 2$ sowie $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$,
- sind die Empfangsworte $\underline{y}_1 = (01), \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ \underline{y}_7 = (11)$ in den Rechtecken angegeben,
- sind alle Fehlergrößen ${\it \Gamma}_0(S_{\mu}), \hspace{0.05cm}\text{ ...} \hspace{0.05cm} , \ {\it \Gamma}_4(S_{\mu})$ bereits eingetragen.
Beispielsweise ergibt sich die Fehlergröße ${\it \Gamma}_4(S_0)$ mit $\underline{y}_4 = (01)$ als das Minimum der beiden Vergleichswerte
- ${\it \Gamma}_3(S_0) + d_{\rm H}((00), \ (01)) = 3 + 1 = 4$, und
- ${\it \Gamma}_3(S_2) + d_{\rm H}((11), \ (01)) = 2 + 1 = 3$.
Der überlebende Zweig – hier von ${\it \Gamma}_3(S_2)$ nach ${\it \Gamma}_4(S_0)$ – ist durchgezogen gezeichnet, der eliminierte Zweig von ${\it \Gamma}_3(S_0)$ nach ${\it \Gamma}_4(S_0)$ punktiert. Rote Pfeile stehen für das Informationsbit $u_i = 0$, blaue Pfeile für $u_i = 1$.
In der Teilaufgabe (4) soll der Zusammenhang zwischen
- der ${\it \Gamma}_i(S_{\mu})$–Minimierung und
- der ${\it \Lambda}_i(S_{\mu})$–Maximierung
herausgearbeitet werden. Hierbei bezeichnet man die Knoten ${\it \Lambda}_i(S_{\mu})$ als Metriken, wobei sich der Metrikzuwachs gegenüber den Vorgängerknoten aus dem Korrelationswert $〈\underline{x}_i\hspace{0.05cm}', \, \underline{y}_i 〉$ ergibt. Näheres zu dieser Thematik finden Sie auf den folgenden Theorieseiten:
- Zusammenhang zwischen Hamming–Distanz und Korrelation,
- Viterbi–Algorithmus, basierend auf Korrelation und Metriken,
- Viterbi–Entscheidung bei nicht–terminierten Faltungscodes.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Decodierung von Faltungscodes.
- Vorerst nicht betrachtet wird die Suche der überlebenden Pfade. Damit beschäftigt sich für das gleiche Beispiel die spätere Aufgabe 3.11.
Fragebogen
Musterlösung
- $${\it \Gamma}_5(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{4}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{4}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \left [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \right ] \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},$$
- $${\it \Gamma}_5(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{4}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{4}(S_2) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \left [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \right ] \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},$$
- $${\it \Gamma}_5(S_2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{4}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{4}(S_3) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] = {\rm min} \left [ 3+2\hspace{0.05cm},\hspace{0.05cm} 2+0 \right ] \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},$$
- $${\it \Gamma}_5(S_3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{4}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{4}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \left [ 3+0\hspace{0.05cm},\hspace{0.05cm} 2+2 \right ] \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
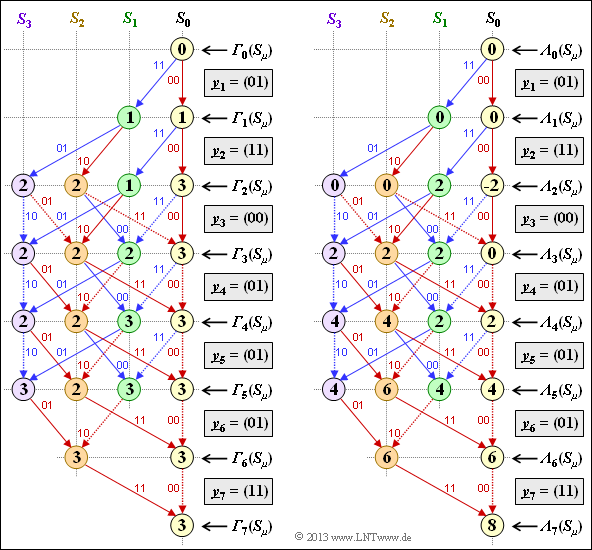
Die linke Grafik zeigt das endgültig ausgewertete ${\it \Gamma}_i(S_{\mu})$–Trellis.
(2) Zum Zeitpunk $i = 6$ ist bereits die Terminierung wirksam und es gibt nur noch zwei Fehlergrößen. Für diese erhält man mit $\underline{y}_6 = (01)$:
- $${\it \Gamma}_6(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{5}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{5}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \left [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \right ] \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},$$
- $${\it \Gamma}_6(S_2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{5}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{5}(S_3) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \left [ 3+2\hspace{0.05cm},\hspace{0.05cm} 3+0 \right ] \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
(3) Der Endwert ergibt sich zu
- $${\it \Gamma}_7(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{6}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big )\hspace{0.05cm},\hspace{0.2cm}{\it \Gamma}_{6}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) \right ] ={\rm min} \left [ 3+2\hspace{0.05cm},\hspace{0.05cm} 3+0 \right ] \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
Beim BSC–Modell kann man aus ${\it \Gamma}_7(S_{\mu}) = 3$ darauf schließen, dass drei Übertragungsfehler aufgetreten sind ⇒ Lösungsvorschläge 1 und 3.
(4) Richtig sind die Aussagen 1 und 2:
- Die Maximierung der Metriken ${\it \Gamma}_i(S_{\mu})$ entsprechend der rechten Grafik liefert das gleiche Ergebnis wie die links dargestellte Minimierung der Fehlergrößen ${\it \Gamma}_i(S_{\mu})$. Auch die überlebenden und gestrichenen Zweige sind in beiden Grafiken identisch.
- Die angegebene Gleichung ist ebenfalls richtig, was hier nur am Beispiel $i = 7$ gezeigt wird:
- $${\it \Lambda}_7(S_0)) = 2 \cdot \left [i - {\it \Gamma}_7(S_0) \right ] = 2 \cdot \left [7 - 3 \right ] \hspace{0.15cm}\underline{= 8}\hspace{0.05cm}.$$
- Die letzte Aussage ist falsch. Vielmehr gilt $〈x_i', \, y_i〉 ∈ \{–2, \, 0, \, +2\}$.
Hinweis: In der Aufgabe 3.11 wird für das gleiche Beispiel die Pfadsuche demonstiert, wobei von den ${\it \Lambda}_i(S_{\mu})$–Metriken entsprechend der rechten Grafik ausgegangen wird.