Difference between revisions of "Aufgaben:Exercise 2.2Z: Power Consideration"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 9: | Line 9: | ||
wobei für die Frequenzen $f_2 ≥ f_1$ gelten soll. | wobei für die Frequenzen $f_2 ≥ f_1$ gelten soll. | ||
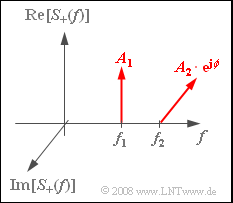
| − | Die Grafik zeigt das Spektrum des analytischen Signals $s_+(t)$, das sich additiv aus den beiden Anteilen $s_{1+}(t)$ und $s_ {2+}(t)$ zusammensetzt. | + | Die Grafik zeigt das Spektrum des analytischen Signals $s_+(t)$, das sich additiv aus den beiden Anteilen $s_{1+}(t)$ und $s_ {2+}(t)$ zusammensetzt. |
| − | Unter der Sendeleistung $P_{\rm S}$ soll hier der quadratische Mittelwert des Signals $s(t)$ verstanden werden, gemittelt über eine möglichst große Messdauer: | + | Unter der Sendeleistung $P_{\rm S}$ soll hier der quadratische Mittelwert des Signals $s(t)$ verstanden werden, gemittelt über eine möglichst große Messdauer: |
:$$P_{\rm S} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {s^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | :$$P_{\rm S} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {s^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | ||
| − | Beschreibt $s(t)$ einen Spannungsverlauf, so besitzt $P_{\rm S}$ nach dieser Definition die Einheit $\rm V^2$ und bezieht sich auf den Widerstand $R = 1 \ \rm Ω$. Die Division durch $R$ liefert die physikalische Leistung in $\rm W$. | + | Beschreibt $s(t)$ einen Spannungsverlauf, so besitzt $P_{\rm S}$ nach dieser Definition die Einheit $\rm V^2$ und bezieht sich auf den Widerstand $R = 1 \ \rm Ω$. Die Division durch $R$ liefert die physikalische Leistung in $\rm W$. |
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband-Amplitudenmodulation]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband-Amplitudenmodulation]]. |
| − | *Bezug genommen wird auch auf das Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. | + | *Bezug genommen wird auch auf das Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. |
| − | *Verwenden Sie die Zahlenwerte $A_1 = 2\ \rm V$, $A_2 = 1 \ \rm V$ und $R = 50 \ \rm Ω$. | + | *Verwenden Sie die Zahlenwerte $A_1 = 2\ \rm V$, $A_2 = 1 \ \rm V$ und $R = 50 \ \rm Ω$. |
| Line 27: | Line 30: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie die Leistung des Cosinussignals $s_1(t)$. | + | {Berechnen Sie die Leistung des Cosinussignals $s_1(t)$. |
|type="{}"} | |type="{}"} | ||
$P_1 \ = \ $ { 2 3% } $\ \rm V^{ 2 }$ | $P_1 \ = \ $ { 2 3% } $\ \rm V^{ 2 }$ | ||
| − | {Es gelte $R = 50 \ \rm Ω$. Wie groß ist die physikalische Leistung des Signals $s_1(t)$? | + | {Es gelte $R = 50 \ \rm Ω$. Wie groß ist die physikalische Leistung des Signals $s_1(t)$? |
|type="{}"} | |type="{}"} | ||
$P_1 \ = \ $ { 40 3% } $\ \text{mW}$ | $P_1 \ = \ $ { 40 3% } $\ \text{mW}$ | ||
| − | {Wie groß ist die Leistung der phasenverschobenen Schwingung $s_2(t)$? | + | {Wie groß ist die Leistung der phasenverschobenen Schwingung $s_2(t)$? |
|type="{}"} | |type="{}"} | ||
$P_2 \ = \ $ { 0.5 3% } $\ \rm V^{ 2 }$ | $P_2 \ = \ $ { 0.5 3% } $\ \rm V^{ 2 }$ | ||
| − | {Wie groß ist die Leistung des Summensignals $s(t)$ unter der Bedingung $f_2 ≠ f_1$? | + | {Wie groß ist die Leistung des Summensignals $s(t)$ unter der Bedingung $f_2 ≠ f_1$? |
|type="{}"} | |type="{}"} | ||
$P_{\rm S} \ = \ $ { 2.5 3% } $\ \rm V^{ 2 }$ | $P_{\rm S} \ = \ $ { 2.5 3% } $\ \rm V^{ 2 }$ | ||
| − | {Welche Leistung erhält man für $f_2 = f_1$ mit $ϕ = 0$, $ϕ = 90^\circ$ und $ϕ = 180^\circ$? | + | {Welche Leistung erhält man für $f_2 = f_1$ mit $ϕ = 0$, $ϕ = 90^\circ$ und $ϕ = 180^\circ$? |
|type="{}"} | |type="{}"} | ||
$ϕ = 0\text{:}\hspace{0.3cm} P_{\rm S} \ = \ $ { 4.5 3% }$\ \rm V^{ 2 }$ | $ϕ = 0\text{:}\hspace{0.3cm} P_{\rm S} \ = \ $ { 4.5 3% }$\ \rm V^{ 2 }$ | ||
Revision as of 15:40, 12 December 2018
Wir betrachten zwei harmonische Schwingungen
- $$ s_1(t) = A_1 \cdot \cos(\omega_{\rm 1} \cdot t ) \hspace{0.05cm},$$
- $$s_2(t) = A_2 \cdot \cos(\omega_{\rm 2} \cdot t + \phi) \hspace{0.05cm},$$
wobei für die Frequenzen $f_2 ≥ f_1$ gelten soll.
Die Grafik zeigt das Spektrum des analytischen Signals $s_+(t)$, das sich additiv aus den beiden Anteilen $s_{1+}(t)$ und $s_ {2+}(t)$ zusammensetzt.
Unter der Sendeleistung $P_{\rm S}$ soll hier der quadratische Mittelwert des Signals $s(t)$ verstanden werden, gemittelt über eine möglichst große Messdauer:
- $$P_{\rm S} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {s^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
Beschreibt $s(t)$ einen Spannungsverlauf, so besitzt $P_{\rm S}$ nach dieser Definition die Einheit $\rm V^2$ und bezieht sich auf den Widerstand $R = 1 \ \rm Ω$. Die Division durch $R$ liefert die physikalische Leistung in $\rm W$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweiseitenband-Amplitudenmodulation.
- Bezug genommen wird auch auf das Kapitel Qualitätskriterien.
- Verwenden Sie die Zahlenwerte $A_1 = 2\ \rm V$, $A_2 = 1 \ \rm V$ und $R = 50 \ \rm Ω$.
Fragebogen
Musterlösung
- $$P_{\rm 1} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {A_1^2 \cdot \cos^2(\omega_{\rm 1} t + \phi_1) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
Zur allgemeineren Berechnung ist die Phase $ϕ_1$ berücksichtigt, die eigentlich $0$ ist. Mit der Gleichung $\cos^{2}(α) = 0.5 · (1 + \cos(2α))$ ergibt sich:
- $$ P_{\rm 1} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {\frac{A_1^2}{2}}\hspace{0.1cm}{\rm d}t + \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {\frac{A_1^2}{2}\cdot \cos(2\omega_{\rm 1} t + 2\phi_1)}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}.$$
Der zweite Term liefert aufgrund der Integration über die Cosinusfunktion, der Division durch $T_{\rm M}$ und dem anschließenden Grenzübergang unabhängig von der Phase $ϕ_1$ keinen Beitrag. Damit erhält man:
- $$P_{\rm 1} = \frac{A_1^2}{2} = \frac{(2\,{\rm V})^2}{2} \hspace{0.15cm}\underline {= 2\,{\rm V}^2}\hspace{0.05cm}.$$
(2) Mit $R = 50\ \rm Ω$ erhält man für die „unnormierte” Leistung:
- $$P_{\rm 1} = \frac{2\,{\rm V}^2}{50\,{\rm \Omega}} \hspace{0.15cm}\underline {= 40\,{\rm mW}}\hspace{0.05cm}.$$
(3) Bereits in der Musterlösung zur Teilaufgabe (1) wurde gezeigt, dass die Phase keinen Einfluss auf die Leistung hat. Daraus folgt:
- $$P_{\rm 2} = \frac{A_2^2}{2} \hspace{0.15cm}\underline {= 0.5\,{\rm V}^2}\hspace{0.05cm}.$$
(4) Zur Leistungsberechnung muss über $s^{2}(t)$ gemittelt werden, wobei gilt:
- $$s^2(t) = s_1^2(t) + s_2^2(t) + 2 \cdot s_1(t) \cdot s_2(t).$$
Aufgrund der Division durch die Messdauer $T_{\rm M}$ und des erforderlichen Grenzübergangs liefert der letzte Term unabhängig von der Phase $ϕ$ keinen Beitrag und man erhält:
- $$P_{\rm S} = P_{\rm 1} + P_{\rm 2} \hspace{0.15cm}\underline {= 2.5\,{\rm V}^2}\hspace{0.05cm}.$$
(5) Mit $f_2 = f_1$ lautet das Spektrum des analytischen Signals:
- $$S_+(f) = (A_{\rm 1} + A_{\rm 2} \cdot {\rm e}^{{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm} \phi})\cdot \delta (f - f_1) \hspace{0.05cm}.$$
Somit ergibt sich das Signal
- $$s(t) = A_3 \cdot \cos(\omega_{\rm 1} t + \phi_3) \hspace{0.05cm},$$
dessen Phase $ϕ_3$ für die Leistungsberechnung keine Rolle spielt. Die Amplitude dieses Signals ist
- $$A_3 = \sqrt{ \left(A_1 + A_2 \cdot \cos(\phi)\right)^2 + A_2^2 \cdot \sin^2(\phi)} = \sqrt{ A_1^2 + A_2^2 + 2 \cdot A_1 \cdot A_2 \cdot \cos(\phi)}\hspace{0.05cm}.$$
- Für $ϕ = 0$ addieren sich die Amplituden skalar:
- $$A_3 = \sqrt{ A_1^2 + A_2^2 + 2 \cdot A_1 \cdot A_2 } = A_1 + A_2 = 3\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} \hspace{0.15cm}\underline {= 4.5\,{\rm V}^2}\hspace{0.05cm}.$$
- Dagegen addieren sich die Amplituden für $ϕ = 90°$ vektoriell ⇒ gleiches Ergebnis wie in der Teilaufgabe (4):
- $$ A_3 = \sqrt{ A_1^2 + A_2^2 } = \sqrt{5}\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} = \frac{5\,{\rm V}^2}{2}\hspace{0.15cm}\underline {= 2.5\,{\rm V}^2}\hspace{0.05cm}.$$
- Für $ϕ = 180°$ überlagern sich die Cosinusschwingungen destruktiv:
- $$A_3 = A_1 - A_2 = 1\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} \hspace{0.15cm}\underline {= 0.5\,{\rm V}^2}\hspace{0.05cm}.$$