Difference between revisions of "Aufgaben:Exercise 5.2: Error Correlation Function"
m (Textersetzung - „* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Beschreibungsgrößen digitaler Kanalmodelle}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Beschreibungsgrößen digitaler Kanalmodelle}} | ||
| − | [[File:P_ID1854__Dig_A_5_2_version1.png|right|frame|Wahrscheinlichkeiten der Fehlerabstände und | + | [[File:P_ID1854__Dig_A_5_2_version1.png|right|frame|Wahrscheinlichkeiten der Fehlerabstände und FKF]] |
| − | Zur Charakterisierung von digitalen Kanalmodellen verwendet man unter | + | Zur Charakterisierung von digitalen Kanalmodellen verwendet man unter anderem |
* die Fehlerkorrelationsfunktion (FKF) | * die Fehlerkorrelationsfunktion (FKF) | ||
| − | :$$\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + | + | :$$\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + |
| − | k}]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$ | + | k}\big]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$ |
* die Fehlerabstandswahrscheinlichkeiten | * die Fehlerabstandswahrscheinlichkeiten | ||
| Line 13: | Line 13: | ||
Hierbei bezeichnen: | Hierbei bezeichnen: | ||
| − | * $〈e_{\rm \nu}〉$ ist die Fehlerfolge mit $e_{\rm \nu} ∈ \{0, 1\}$. | + | * $〈e_{\rm \nu}〉$ ist die Fehlerfolge mit $e_{\rm \nu} ∈ \{0, 1\}$. |
| − | * $a$ gibt den Fehlerabstand an. | + | * $a$ gibt den Fehlerabstand an. |
| − | Zwei direkt aufeinanderfolgende Bitfehler werden somit durch den Fehlerabstand $a = 1$ gekennzeichnet. | + | Zwei direkt aufeinanderfolgende Bitfehler werden somit durch den Fehlerabstand $a = 1$ gekennzeichnet. |
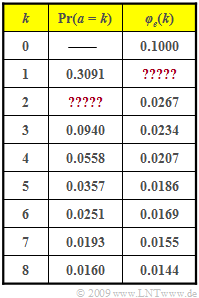
| − | Die Tabelle zeigt beispielhafte Werte der Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a = k)$ sowie der Fehlerkorrelationsfunktion $\varphi_e(k)$. Einige Angaben fehlen in der Tabelle. Diese Werte sollen aus den gegebenen Werten berechnet werden. | + | Die Tabelle zeigt beispielhafte Werte der Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a = k)$ sowie der Fehlerkorrelationsfunktion $\varphi_e(k)$. |
| + | *Einige Angaben fehlen in der Tabelle. | ||
| + | *Diese Werte sollen aus den gegebenen Werten berechnet werden. | ||
| − | '' | + | |
| − | * Die Aufgabe behandelt den Lehrstoff des Kapitels [[Digitalsignal%C3%BCbertragung/Beschreibungsgr%C3%B6%C3%9Fen_digitaler_Kanalmodelle| Beschreibungsgrößen digitaler Kanalmodelle]]. | + | |
| + | |||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe behandelt den Lehrstoff des Kapitels [[Digitalsignal%C3%BCbertragung/Beschreibungsgr%C3%B6%C3%9Fen_digitaler_Kanalmodelle| Beschreibungsgrößen digitaler Kanalmodelle]]. | ||
| Line 36: | Line 41: | ||
{Welcher Wert ergibt sich für den mittleren Fehlerabstand? | {Welcher Wert ergibt sich für den mittleren Fehlerabstand? | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm E}[a] \ = \ ${ 10 3% } | + | ${\rm E}\big[a\big] \ = \ ${ 10 3% } |
| − | {Berechnen Sie den Wert der Fehlerkorrelationsfunktion (FKF) für $k = 1$. | + | {Berechnen Sie den Wert der Fehlerkorrelationsfunktion (FKF) für $k = 1$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 1) \ = \ ${ 0.0309 3% } | $\varphi_e(k = 1) \ = \ ${ 0.0309 3% } | ||
| − | {Welche Näherung gilt für die Wahrscheinlichkeit des Fehlerabstands $a = 2$? | + | {Welche Näherung gilt für die Wahrscheinlichkeit des Fehlerabstands $a = 2$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(a = 2) \ = \ ${ 0.1715 3% } | ${\rm Pr}(a = 2) \ = \ ${ 0.1715 3% } | ||
Revision as of 12:26, 25 March 2019
Zur Charakterisierung von digitalen Kanalmodellen verwendet man unter anderem
- die Fehlerkorrelationsfunktion (FKF)
- $$\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$
- die Fehlerabstandswahrscheinlichkeiten
- $${\rm Pr}( a =k) \hspace{0.05cm}, \hspace{0.2cm} k \ge 1\hspace{0.05cm}.$$
Hierbei bezeichnen:
- $〈e_{\rm \nu}〉$ ist die Fehlerfolge mit $e_{\rm \nu} ∈ \{0, 1\}$.
- $a$ gibt den Fehlerabstand an.
Zwei direkt aufeinanderfolgende Bitfehler werden somit durch den Fehlerabstand $a = 1$ gekennzeichnet.
Die Tabelle zeigt beispielhafte Werte der Fehlerabstandswahrscheinlichkeiten ${\rm Pr}(a = k)$ sowie der Fehlerkorrelationsfunktion $\varphi_e(k)$.
- Einige Angaben fehlen in der Tabelle.
- Diese Werte sollen aus den gegebenen Werten berechnet werden.
Hinweis:
- Die Aufgabe behandelt den Lehrstoff des Kapitels Beschreibungsgrößen digitaler Kanalmodelle.
Fragebogen
Musterlösung
- $$\varphi_{e}(k = 0) = {\rm E}[e_{\nu}^2 ]= {\rm E}[e_{\nu} ]= p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm M}\hspace{0.15cm}\underline { = 0.1} \hspace{0.05cm}.$$
(2) Der mittlere Fehlerabstand ist gleich dem Kehrwert der mittleren Fehlerwahrscheinlichkeit. Das heißt: $E[a] = 1/p_{\rm M} \ \underline {= 10}$.
(3) Nach der Definitionsgleichung und dem Satz von Bayes erhält man folgendes Ergebnis:
- $$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}] = {\rm E}[(e_{\nu} = 1) \cdot (e_{\nu + 1}=1)]={\rm Pr}(e_{\nu + 1}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot {\rm Pr}(e_{\nu} = 1) \hspace{0.05cm}.$$
Die erste Wahrscheinlichkeits ist gleich ${\rm Pr}(a = 1)$ und die zweite Wahrscheinlichkeit ist gleich $p_{\rm M}$:
- $$\varphi_{e}(k = 1) = 0.3091 \cdot 0.1\hspace{0.15cm}\underline { = 0.0309} \hspace{0.05cm}.$$
(4) Der FKF–Wert $\varphi_e(k = 2)$ kann (näherungsweise) folgendermaßen interpretiert werden:
- $$\varphi_{e}(k = 2) ={\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = \frac{\varphi_{e}(k = 2)}{p_{\rm M}} = \frac{0.0267}{0.1} = 0.267\hspace{0.05cm}.$$
Diese Wahrscheinlichkeit setzt sich zusammen aus den beiden Möglichkeiten „Zum Zeitpunkt $\nu+1$ tritt ein Fehler auf” sowie „Zum Zeitpunkt $\nu+1$ gibt es keinen Fehler”:
- $${\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = {\rm Pr}( a =1) \cdot {\rm Pr}( a =1) + {\rm Pr}( a =2)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}( a =2)= 0.267 - 0.3091^2 \hspace{0.15cm}\underline {= 0.1715}\hspace{0.05cm}.$$
Bei der Rechnung wurde davon ausgegangen, dass die einzelnen Fehlerabstände statistisch voneinander unabhängig sind.
- Diese Annahme gilt allerdings nur für eine besondere Klasse von Kanalmodellen, die man als „erneuernd” bezeichnet.
- Das hier betrachtete Bündelfehlermodell erfüllt diese Bedingung nicht.
- Die tatsächliche Wahrscheinlichkeit ${\rm Pr}(a = 2) = 0.1675$ weicht deshalb vom hier berechneten Wert ($0.1715$) geringfügig ab.