Difference between revisions of "Mobile Communications/Non-Frequency-Selective Fading With Direct Component"
| Line 8: | Line 8: | ||
== Kanalmodell und Rice–WDF == | == Kanalmodell und Rice–WDF == | ||
<br> | <br> | ||
| − | Die [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Allgemeine_Beschreibung_des_Mobilfunkkanals| Rayleigh–Verteilung]] beschreibt den Mobilfunkkanal unter der Annahme, dass kein direkter Pfad vorhanden ist und sich somit der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ allein aus diffus gestreuten Komponenten zusammensetzt. | + | Die [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Allgemeine_Beschreibung_des_Mobilfunkkanals| Rayleigh–Verteilung]] beschreibt den Mobilfunkkanal unter der Annahme, dass kein direkter Pfad vorhanden ist und sich somit der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ allein aus diffus gestreuten Komponenten zusammensetzt. |
| − | Bei Vorhandensein einer Direktkomponente (englisch: <i>Line of Sight</i>, LoS) muss man im Modell zu den mittelwertfreien Gaußprozessen $x(t)$ und $y(t)$ noch Gleichkomponenten $x_0$ und/oder $y_0$ hinzufügen: | + | Bei Vorhandensein einer Direktkomponente (englisch: <i>Line of Sight</i>, LoS) muss man im Modell zu den mittelwertfreien Gaußprozessen $x(t)$ und $y(t)$ noch Gleichkomponenten $x_0$ und/oder $y_0$ hinzufügen: |
::<math>x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},</math> | ::<math>x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},</math> | ||
| Line 17: | Line 17: | ||
z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.</math> | z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.</math> | ||
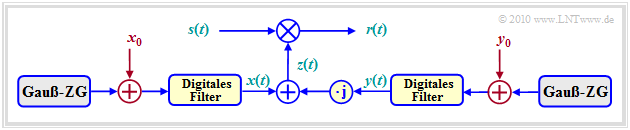
| − | Die Grafik zeigt | + | Die Grafik zeigt dieses '''Rice–Fading–Kanalmodell'''. Als Sonderfall ergibt sich daraus das Rayleigh–Modell, wenn man $x_0 = y_0= 0$ setzt.<br> |
[[File:P ID2126 Mob T 1 4 S1 v3.png|center|frame|Rice-Fading-Kanalmodell|class=fit]] | [[File:P ID2126 Mob T 1 4 S1 v3.png|center|frame|Rice-Fading-Kanalmodell|class=fit]] | ||
| − | Das Rice–Fading–Modell lässt sich wie folgt zusammenfassen, siehe auch [Hin08]<ref name = 'Hin08'>Hindelang, T.: ''Mobile Communications''. Vorlesungsmanuskript. Lehrstuhl für Nachrichtentechnik, TU München, 2008.</ref>: | + | Das Rice–Fading–Modell lässt sich wie folgt zusammenfassen, siehe auch [Hin08]<ref name = 'Hin08'>Hindelang, T.: ''Mobile Communications''. Vorlesungsmanuskript. Lehrstuhl für Nachrichtentechnik, TU München, 2008.</ref>: |
| − | *Der Realteil $x(t)$ ist gaußverteilt mit Mittelwert $x_0$ und Varianz $\sigma ^2$. | + | *Der Realteil $x(t)$ ist gaußverteilt mit Mittelwert $x_0$ und Varianz $\sigma ^2$. |
| − | *Der Imaginärteil $y(t)$ ist ebenfalls gaußverteilt (Mittelwert $y_0$, gleiche Varianz $\sigma ^2$ | + | *Der Imaginärteil $y(t)$ ist ebenfalls gaußverteilt $($Mittelwert $y_0$, gleiche Varianz $\sigma ^2)$ sowie unabhängig von $x(t)$.<br> |
| − | *Für $z_0 \ne 0$ ist der Betrag $|z(t)|$ [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung| riceverteilt]], woraus die Bezeichnung „<i>Rice–Fading</i>” herrührt. | + | *Für $z_0 \ne 0$ ist der Betrag $|z(t)|$ [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung| riceverteilt]], woraus die Bezeichnung „<i>Rice–Fading</i>” herrührt. |
| − | *Zur Vereinfachung der Schreibweise setzen wir $|z(t)| = a(t)$. Für $a < 0$ ist die Betrags–WDF $f_a(a) \equiv 0$, für $a \ge 0$ gilt folgende Gleichung, wobei $I_0$ die <i>modifizierte Bessel–Funktion</i> nullter Ordnung bezeichnet: | + | *Zur Vereinfachung der Schreibweise setzen wir $|z(t)| = a(t)$. Für $a < 0$ ist die Betrags–WDF $f_a(a) \equiv 0$, für $a \ge 0$ gilt folgende Gleichung, wobei $\rm I_0(\cdot)$ die <i>modifizierte Bessel–Funktion</i> nullter Ordnung bezeichnet: |
::<math>f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} \big [ -\frac{a^2 + |z_0|^2}{2\sigma^2}\big ] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = | ::<math>f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} \big [ -\frac{a^2 + |z_0|^2}{2\sigma^2}\big ] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = | ||
| Line 32: | Line 32: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Der Mobilfunkkanal ist um so besser für die Digitalsignalübertragung geeignet, je größer die „Direktpfadleistung” $(|z_0|^2)$ gegenüber den Leistungen der Streukomponenten $(2\sigma^2)$ ist.<br> | + | *Der Mobilfunkkanal ist um so besser für die Digitalsignalübertragung geeignet, je größer die „Direktpfadleistung” $(|z_0|^2)$ gegenüber den Leistungen der Streukomponenten $(2\sigma^2)$ ist.<br> |
| − | *Ist $|z_0| \gg \sigma$ (Faktor 3 oder mehr), so kann die Rice–WDF mit guter Näherung durch eine Gaußverteilung mit | + | *Ist $|z_0| \gg \sigma$ (Faktor $3$ oder mehr), so kann die Rice–WDF mit guter Näherung durch eine Gaußverteilung mit Mittelwert $|z_0|$ und Streuung $\sigma$ angenähert werden.<br> |
| − | *Im Gegensatz zum <i>Rayleigh–Fading</i> ⇒ $z_0 \equiv 0$ ist die Phase bei <i>Rice–Fading</i> nicht gleichverteilt, sondern es gibt eine Vorzugsrichtung $\phi_0 = \arctan(y_0/x_0)$. Oft setzt man $y_0 = 0$ ⇒ $\phi_0 = 0$.<br> | + | *Im Gegensatz zum <i>Rayleigh–Fading</i> ⇒ $z_0 \equiv 0$ ist die Phase bei <i>Rice–Fading</i> nicht gleichverteilt, sondern es gibt eine Vorzugsrichtung $\phi_0 = \arctan(y_0/x_0)$. Oft setzt man $y_0 = 0$ ⇒ $\phi_0 = 0$.<br> |
== Beispielhafte Signalverläufe bei Rice–Fading== | == Beispielhafte Signalverläufe bei Rice–Fading== | ||
| Line 42: | Line 42: | ||
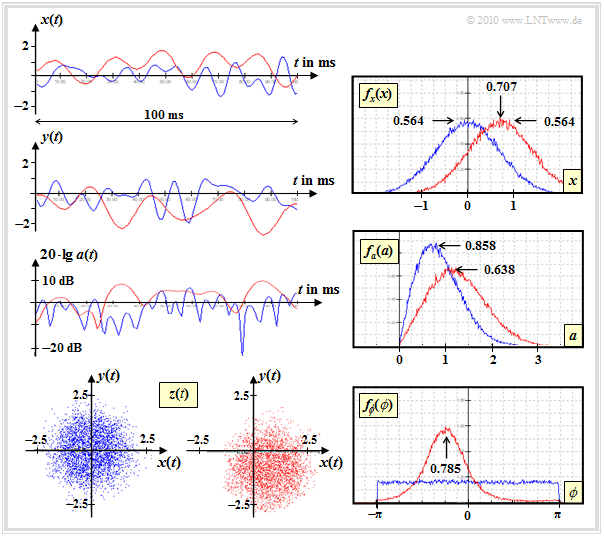
Die Grafik zeigt Signalverläufe und Dichtefunktionen zweier Mobilfunkkanäle: | Die Grafik zeigt Signalverläufe und Dichtefunktionen zweier Mobilfunkkanäle: | ||
[[File:P ID2129 Mob T 1 4 S2 v1.png|right|frame|Vergleich von Rayleigh-Fading (blau) und Rice-Fading (rot)|class=fit]] | [[File:P ID2129 Mob T 1 4 S2 v1.png|right|frame|Vergleich von Rayleigh-Fading (blau) und Rice-Fading (rot)|class=fit]] | ||
| − | *Rayleigh–Fading (blaue Kurven) <br>mit ${\rm E}\big [|z(t))|^2\big ] = 2 \cdot \sigma^2 = 1$,<br> | + | *Rayleigh–Fading (blaue Kurven) <br>mit ${\rm E}\big [|z(t))|^2\big ] = 2 \cdot \sigma^2 = 1$,<br> |
| − | *Rice–Fading (rote Kurven) <br>mit gleichem $\sigma$ sowie $x_0 = 0.707$ und $y_0 = -0.707$. | + | *Rice–Fading (rote Kurven) <br>mit gleichem $\sigma$ sowie $x_0 = 0.707$ und $y_0 = -0.707$. |
| − | Für die Erzeugung der Signalausschnitte mit dem oben gezeigten Modell wurde für Rayleigh und für Rice die [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Dopplerfrequenz_und_deren_Verteilung| maximale Dopplerfrequenz]] $f_\text{D, max} = 100 \ \rm Hz$ zugrundegelegt. | + | |
| − | + | Für die Erzeugung der Signalausschnitte mit dem oben gezeigten Modell wurde für Rayleigh und für Rice die [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Dopplerfrequenz_und_deren_Verteilung| maximale Dopplerfrequenz]] $f_\text{D, max} = 100 \ \rm Hz$ zugrundegelegt. | |
| − | Autokorrelationsfunktion (AKF) und Leistungsdichtespektrum (LDS) von Rayleigh und Rice unterscheiden sich nur geringfügig. Es gilt: | + | |
| + | |||
| + | Autokorrelationsfunktion (AKF) und Leistungsdichtespektrum (LDS) von Rayleigh und Rice unterscheiden sich bei ansonstern angepassten Parameterwerten nur geringfügig. Es gilt: | ||
::<math>\varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.5cm} = \varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} \hspace{-0.8cm} + |z_0|^2 \hspace{0.05cm},</math> | ::<math>\varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.5cm} = \varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} \hspace{-0.8cm} + |z_0|^2 \hspace{0.05cm},</math> | ||
| Line 54: | Line 56: | ||
Berücksichtigt ist, dass die Spektraldarstellung eines Gleichanteils zu einer Diracfunktion führt.<br> | Berücksichtigt ist, dass die Spektraldarstellung eines Gleichanteils zu einer Diracfunktion führt.<br> | ||
| − | |||
<br clear= all> | <br clear= all> | ||
Zu dieser Grafik ist anzumerken: | Zu dieser Grafik ist anzumerken: | ||
| − | *Die Realteile $x(t)$ von Rayleigh (blau) | + | *Die Realteile $x(t)$ von Rayleigh (blau) und Rice (rot) unterscheiden sich durch die Konstante $x_0 = 0.707$. Die statistischen Eigenschaften sind ansonsten gleich: Gaußsche WDF $f_x(x)$ mit Streuung $\sigma = 0.707$, entweder mittelwertfrei (Rayleigh) oder mit Mittelwert $x_0$ (Rice).<br> |
| − | *Im Imaginärteil $y(t)$ erkennt man bei Rice zusätzlich die Gleichkomponente $y_0 = -0.707$. Die (nicht dargestellte) WDF $f_y(y)$ ist somit eine Gaußkurve mit der Streuung $\sigma = 0.707$ um den Mittelwert $ y_0 = -0.707$, also achsensymmetrisch zur skizzierten WDF $f_x(x)$.<br> | + | *Im Imaginärteil $y(t)$ erkennt man bei Rice zusätzlich die Gleichkomponente $y_0 = -0.707$. Die (hier nicht dargestellte) WDF $f_y(y)$ ist somit eine Gaußkurve mit der Streuung $\sigma = 0.707$ um den Mittelwert $ y_0 = -0.707$, also achsensymmetrisch zur skizzierten WDF $f_x(x)$.<br> |
| − | *Die (logarithmische) Betragsdarstellung ⇒ $a(t) =|z(t)|$ zeigt, dass die rote Kurve meist oberhalb der blauen liegt. Diese Tatsache ist auch aus der WDF $f_a(a)$ ablesbar. | + | *Die (logarithmische) Betragsdarstellung ⇒ $a(t) =|z(t)|$ zeigt, dass die rote Kurve meist oberhalb der blauen liegt. Diese Tatsache ist auch aus der WDF $f_a(a)$ ablesbar. |
*Beim Rice–Kanal ist die Fehlerwahrscheinlichkeit unter Berücksichtigung von AWGN–Rauschen niedriger als bei Rayleigh, da der Empfänger über den Rice–Direktpfad viel nutzbare Energie erhält.<br> | *Beim Rice–Kanal ist die Fehlerwahrscheinlichkeit unter Berücksichtigung von AWGN–Rauschen niedriger als bei Rayleigh, da der Empfänger über den Rice–Direktpfad viel nutzbare Energie erhält.<br> | ||
| − | *Die WDF $f_\phi(\phi)$ zeigt den Vorzugswinkel $\phi \approx 45^\circ$ des Rice–Kanals. Der komplexe Faktor $z(t)$ befindet sich wegen $x_0 > 0$ und $y_0 < 0$ großteils im vierten Quadranten, während beim Rayleigh–Kanal alle Quadranten gleichwahrscheinlich sind.<br> | + | *Die WDF $f_\phi(\phi)$ zeigt den Vorzugswinkel $\phi \approx 45^\circ$ des vorliegenden Rice–Kanals. Der komplexe Faktor $z(t)$ befindet sich wegen $x_0 > 0$ und $y_0 < 0$ großteils im vierten Quadranten, während beim Rayleigh–Kanal alle Quadranten gleichwahrscheinlich sind.<br> |
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
Revision as of 14:02, 6 April 2019
Contents
Kanalmodell und Rice–WDF
Die Rayleigh–Verteilung beschreibt den Mobilfunkkanal unter der Annahme, dass kein direkter Pfad vorhanden ist und sich somit der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ allein aus diffus gestreuten Komponenten zusammensetzt.
Bei Vorhandensein einer Direktkomponente (englisch: Line of Sight, LoS) muss man im Modell zu den mittelwertfreien Gaußprozessen $x(t)$ und $y(t)$ noch Gleichkomponenten $x_0$ und/oder $y_0$ hinzufügen:
- \[x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},\]
- \[z(t) = x(t) + {\rm j} \cdot y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} z(t) +z_0 \hspace{0.05cm},\hspace{0.2cm} z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.\]
Die Grafik zeigt dieses Rice–Fading–Kanalmodell. Als Sonderfall ergibt sich daraus das Rayleigh–Modell, wenn man $x_0 = y_0= 0$ setzt.
Das Rice–Fading–Modell lässt sich wie folgt zusammenfassen, siehe auch [Hin08][1]:
- Der Realteil $x(t)$ ist gaußverteilt mit Mittelwert $x_0$ und Varianz $\sigma ^2$.
- Der Imaginärteil $y(t)$ ist ebenfalls gaußverteilt $($Mittelwert $y_0$, gleiche Varianz $\sigma ^2)$ sowie unabhängig von $x(t)$.
- Für $z_0 \ne 0$ ist der Betrag $|z(t)|$ riceverteilt, woraus die Bezeichnung „Rice–Fading” herrührt.
- Zur Vereinfachung der Schreibweise setzen wir $|z(t)| = a(t)$. Für $a < 0$ ist die Betrags–WDF $f_a(a) \equiv 0$, für $a \ge 0$ gilt folgende Gleichung, wobei $\rm I_0(\cdot)$ die modifizierte Bessel–Funktion nullter Ordnung bezeichnet:
- \[f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} \big [ -\frac{a^2 + |z_0|^2}{2\sigma^2}\big ] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
- Der Mobilfunkkanal ist um so besser für die Digitalsignalübertragung geeignet, je größer die „Direktpfadleistung” $(|z_0|^2)$ gegenüber den Leistungen der Streukomponenten $(2\sigma^2)$ ist.
- Ist $|z_0| \gg \sigma$ (Faktor $3$ oder mehr), so kann die Rice–WDF mit guter Näherung durch eine Gaußverteilung mit Mittelwert $|z_0|$ und Streuung $\sigma$ angenähert werden.
- Im Gegensatz zum Rayleigh–Fading ⇒ $z_0 \equiv 0$ ist die Phase bei Rice–Fading nicht gleichverteilt, sondern es gibt eine Vorzugsrichtung $\phi_0 = \arctan(y_0/x_0)$. Oft setzt man $y_0 = 0$ ⇒ $\phi_0 = 0$.
Beispielhafte Signalverläufe bei Rice–Fading
Die Grafik zeigt Signalverläufe und Dichtefunktionen zweier Mobilfunkkanäle:
- Rayleigh–Fading (blaue Kurven)
mit ${\rm E}\big [|z(t))|^2\big ] = 2 \cdot \sigma^2 = 1$,
- Rice–Fading (rote Kurven)
mit gleichem $\sigma$ sowie $x_0 = 0.707$ und $y_0 = -0.707$.
Für die Erzeugung der Signalausschnitte mit dem oben gezeigten Modell wurde für Rayleigh und für Rice die maximale Dopplerfrequenz $f_\text{D, max} = 100 \ \rm Hz$ zugrundegelegt.
Autokorrelationsfunktion (AKF) und Leistungsdichtespektrum (LDS) von Rayleigh und Rice unterscheiden sich bei ansonstern angepassten Parameterwerten nur geringfügig. Es gilt:
- \[\varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.5cm} = \varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} \hspace{-0.8cm} + |z_0|^2 \hspace{0.05cm},\]
- \[ {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.5cm} = {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} \hspace{-0.8cm} + |z_0|^2 \cdot \delta (f_{\rm D}) \hspace{0.05cm}.\]
Berücksichtigt ist, dass die Spektraldarstellung eines Gleichanteils zu einer Diracfunktion führt.
Zu dieser Grafik ist anzumerken:
- Die Realteile $x(t)$ von Rayleigh (blau) und Rice (rot) unterscheiden sich durch die Konstante $x_0 = 0.707$. Die statistischen Eigenschaften sind ansonsten gleich: Gaußsche WDF $f_x(x)$ mit Streuung $\sigma = 0.707$, entweder mittelwertfrei (Rayleigh) oder mit Mittelwert $x_0$ (Rice).
- Im Imaginärteil $y(t)$ erkennt man bei Rice zusätzlich die Gleichkomponente $y_0 = -0.707$. Die (hier nicht dargestellte) WDF $f_y(y)$ ist somit eine Gaußkurve mit der Streuung $\sigma = 0.707$ um den Mittelwert $ y_0 = -0.707$, also achsensymmetrisch zur skizzierten WDF $f_x(x)$.
- Die (logarithmische) Betragsdarstellung ⇒ $a(t) =|z(t)|$ zeigt, dass die rote Kurve meist oberhalb der blauen liegt. Diese Tatsache ist auch aus der WDF $f_a(a)$ ablesbar.
- Beim Rice–Kanal ist die Fehlerwahrscheinlichkeit unter Berücksichtigung von AWGN–Rauschen niedriger als bei Rayleigh, da der Empfänger über den Rice–Direktpfad viel nutzbare Energie erhält.
- Die WDF $f_\phi(\phi)$ zeigt den Vorzugswinkel $\phi \approx 45^\circ$ des vorliegenden Rice–Kanals. Der komplexe Faktor $z(t)$ befindet sich wegen $x_0 > 0$ und $y_0 < 0$ großteils im vierten Quadranten, während beim Rayleigh–Kanal alle Quadranten gleichwahrscheinlich sind.
Aufgaben zum Kapitel
Aufgabe 1.6: AKF und LDS bei Rice–Fading
Aufgabe 1.6Z: Rayleigh und Rice im Vergleich
Aufgabe 1.7: WDF des Rice–Fadings
Quellenverzeichnis
- ↑ Hindelang, T.: Mobile Communications. Vorlesungsmanuskript. Lehrstuhl für Nachrichtentechnik, TU München, 2008.