Difference between revisions of "Applets:Physical Signal & Analytic Signal"
| Line 232: | Line 232: | ||
'''(7)''' Now applies $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 90^\circ$. | '''(7)''' Now applies $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 90^\circ$. | ||
| − | :Which constellation is described here? What changes with $A_{\rm U} = 0.8\ \text{V}$ | + | :Which constellation is described here? What changes with $A_{\rm U} = 0.8\ \text{V}$ und $A_{\rm O} = 0$?}} |
| − | ::In both cases, it is a [[Modulationsverfahren/Einseitenbandmodulation|Einseitenbandmodulation]] '''(ESB–AM)''' with the modulation degree $\mu = 0.8$ (in ESB we denote the degree of modulation with $\mu$ instead | + | ::In both cases, it is a [[Modulationsverfahren/Einseitenbandmodulation|Einseitenbandmodulation]] '''(ESB–AM)''' with the modulation degree $\mu = 0.8$ (in ESB we denote the degree of modulation with $\mu$ instead $m$). he carrier signal is cosinusoidal and the message signal is sinusoidal. |
| − | ::$A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ is an OSB | + | :: $A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ is an OSB modulation. The green pointer is missing and the blue pointer rotates faster compared to the red carrier. |
| − | ::$A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ is a USB | + | :: $A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ is a USB modulation. The blue pointer is missing and the green pointer rotates slower compared to the red carrier. |
| Line 244: | Line 244: | ||
'''(8)''' Now applies $\text{Red:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blue:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$. | '''(8)''' Now applies $\text{Red:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blue:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$. | ||
| − | :Which constellation could be described here? Which figure is given for the equivalent | + | :Which constellation could be described here? Which figure is given for the equivalent lowpass–signal $x_{\rm TP}(t)$? ⇒ „locus”?}} |
| − | ::It could be a ZSB–AM of a sinusoidal signal with cosinusoidal carrier and modulation degree $m=0.8$, in which the upper sideband is attenuated by a factor of 2. The equivalent | + | ::It could be a ZSB–AM of a sinusoidal signal with cosinusoidal carrier and modulation degree $m=0.8$, in which the upper sideband is attenuated by a factor of 2. The equivalent lowpass–signal $x_{\rm TP}(t)$ has an elliptical course in the complex plane. |
| Line 290: | Line 290: | ||
==About the Authors== | ==About the Authors== | ||
| − | + | This interactive calculation was designed and realized at the [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] of the [https://www.tum.de/ Technischen Universität München] . | |
| − | * | + | *The original version was created in 2005 by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] as part of her Diploma thesis using „FlashMX–Actionscript” (Supervisor: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | *2018 | + | *In 2018 this Applet was redesigned and updated to „HTML5” by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Xiaohan_Liu_.28Bachelorarbeit_2018.29|Xiaohan Liu]] as part of her Bachelor's thesis (Supervisor: [[Biografien_und_Bibliografien/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]]). |
==Once again: Open Applet in new Tab== | ==Once again: Open Applet in new Tab== | ||
Revision as of 20:07, 10 July 2018
Contents
Applet Description
Dieses Applet zeigt den Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$. Ausgegangen wird stets von einem Bandpass–Signal $x(t)$ mit frequenzdiskretem Spektrum $X(f)$:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
Das physikalische Signal $x(t)$ setzt sich also aus drei harmonischen Schwingungen zusammen, einer Konstellation, die sich zum Beispiel bei der Zweiseitenband-Amplitudenmodulation des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ ergibt. Die Nomenklatur ist ebenfalls an diesen Fall angepasst:
- $x_{\rm O}(t)$ bezeichnet das „Obere Seitenband” mit der Amplitude $A_{\rm O}= A_{\rm N}/2$, der Frequenz $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und der Phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$.
- Entsprechend gilt für das „Untere Seitenband” $x_{\rm U}(t)$ mit $f_{\rm U} = f_{\rm T} + f_{\rm N}$, $A_{\rm U}= A_{\rm O}$ und $\varphi_{\rm U} = -\varphi_{\rm O}$.
Das dazugehörige analytische Signal lautet:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
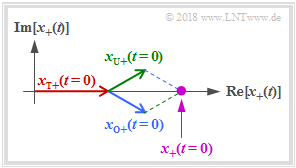
Im Programm dargestellt wird $x_+(t)$ als vektorielle Summe dreier Drehzeiger (alle mit positiver Drehrichtung) als violetter Punkt (siehe beispielhafte Grafik für den Startzeitpunkt $t=0$):
- Der (rote) Zeiger des Trägers $x_{\rm T+}(t)$ mit der Länge $A_{\rm T}$ und der Nullphasenlage $\varphi_{\rm T} = 0$ dreht mit konstanter Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}$ (eine Umdrehung in der Zeit $1/f_{\rm T}$.
- Der (blaue) Zeiger des Oberen Seitenbandes $x_{\rm O+}(t)$ mit der Länge $A_{\rm O}$ und der Nullphasenlage $\varphi_{\rm O}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}$, also etwas schneller als $x_{\rm T+}(t)$.
- Der (grüne) Zeiger des Unteren Seitenbandes $x_{\rm U+}(t)$ mit der Länge $A_{\rm U}$ und der Nullphasenlage $\varphi_{\rm U}$ dreht mit der Winkelgeschwindigkeit $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}$, also etwas langsamer als $x_{\rm T+}(t)$.
Den zeitlichen Verlauf von $x_+(t)$ bezeichnen wir im Folgenden auch als Zeigerdiagramm. Der Zusammenhang zwischen dem physikalischen Bandpass–Signal $x(t)$ und dem dazugehörigen analytischen Signal $x_+(t)$ lautet:
- $$x(t) = {\rm Re}\big [x_+(t)\big ].$$
Hinweis: Die Grafik gilt für $\varphi_{\rm O} = +30^\circ$. Daraus folgt für den Startzeitpunkt $t=0$ der Winkel gegenüber dem Koordinatensystem: $\phi_{\rm O} = -\varphi_{\rm O} = -30^\circ$. Ebenso folgt aus der Nullphanlage $\varphi_{\rm U} = -30^\circ$ des unteren Seitenbandes für den in der komplexen Ebene zu berücksichtigenden Phasenwinkel: $\phi_{\rm U} = +30^\circ$.
Englische Beschreibung (muss noch angepasst werden)
Theoretical Background
Beschreibungsmöglichkeiten von Bandpass-Signalen
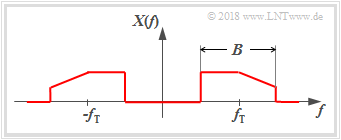
Wir betrachten hier Bandpass-Signale $x(t)$ mit der Eigenschaft, dass deren Spektren $X(f)$ nicht im Bereich um die Frequenz $f = 0$ liegen, sondern um eine Trägerfrequenz $f_{\rm T}$. Meist kann auch davon ausgegangen werden, dass die Bandbreite $B \ll f_{\rm T}$ ist.
Die Grafik zeigt ein solches Bandpass–Spektrum $X(f)$. Unter der Annahme, dass das zugehörige $x(t)$ ein physikalisches Signal und damit reell ist, ergibt sich für die Spektralfunktion $X(f)$ eine Symmetrie bezüglich der Frequenz $f = 0$. Ist $x(t)$ eine gerade Funktion ⇒ $x(-t)=x(t)$, so ist auch $X(f)$ reell und gerade.
Neben dem physikalischen Signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$ verwendet man zur Beschreibung von Bandpass-Signalen gleichermaßen:
- das analytische Signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, wie im nächsten Unterabschnitt beschrieben,
- das äquivalente Tiefpass–Signal $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$, siehe Applet Physikalisches Signal und Äquivalentes Tiefpass–Signal.
Analytisches Signal – Spektralfunktion
Das zum physikalischen Signal $x(t)$ gehörige analytische Signal $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt:
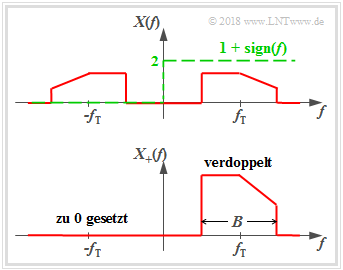
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$
Die so genannte Signumfunktion ist dabei für positive Werte von $f$ gleich $+1$ und für negative $f$–Werte gleich $-1$.
- Der (beidseitige) Grenzwert liefert $\sign(0) = 0$.
- Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt.
Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$: Das tatsächliche BP–Spektrum $X(f)$ wird
- bei den positiven Frequenzen verdoppelt, und
- bei den negativen Frequenzen zu Null gesetzt.
Aufgrund der Unsymmetrie von $X_+(f)$ bezüglich der Frequenz $f = 0$ kann man bereits jetzt schon sagen, dass die Zeitfunktion $x_+(t)$ bis auf einen trivialen Sonderfall $x_+(t)= 0 \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X_+(f)= 0$ stets komplex ist.
Analytisches Signal – Zeitverlauf
An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen.
$\text{Definition:}$ Für die Hilberttransformierte $ {\rm H}\left\{x(t)\right\}$ einer Zeitfunktion $x(t)$ gilt:
- $$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau} }\hspace{0.15cm} {\rm d}\tau.$$
Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des Cauchy–Hauptwertsatzes ausgewertet werden.
Entsprechend gilt im Frequenzbereich:
- $$Y(f) = {\rm -j \cdot sign}(f) \cdot X(f) \hspace{0.05cm} .$$
Das obige Ergebnis lässt sich mit dieser Definition wie folgt zusammenfassen:
- Man erhält aus dem physikalischen BP–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil gemäß der Hilberttransformierten hinzufügt:
- $$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$
- $\text{H}\{x(t)\}$ verschwindet nur für den Fall $x(t) = \rm const.$ ⇒ Gleichsignal. Bei allen anderen Signalformen ist somit das analytische Signal $x_+(t)$ komplex.
- Aus dem analytischen Signal $x_+(t)$ kann das physikalische Bandpass–Signal in einfacher Weise durch Realteilbildung ermittelt werden:
- $$x(t) = {\rm Re}\big[x_+(t)\big] .$$
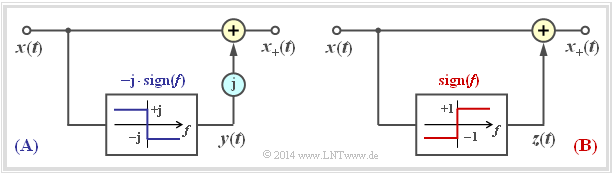
$\text{Beispiel 1:}$ Das Prinzip der Hilbert–Transformation wird durch die nachfolgende Grafik nochmals verdeutlicht:
- Nach der linken Darstellung $\rm(A)$ kommt man vom physikalischen Signal $x(t)$ zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil ${\rm j} \cdot y(t)$ hinzufügt.
- Hierbei ist $y(t) = {\rm H}\left\{x(t)\right\}$ eine reelle Zeitfunktion, die sich im Spektralbereich durch die Multiplikation des Spektrums $X(f)$ mit $\rm {- j} \cdot \sign(f)$ angeben lässt.
Die rechte Darstellung $\rm(B)$ ist äquivalent zu $\rm(A)$. Nun gilt $x_+(t) = x(t) + z(t)$ mit der rein imaginären Funktion $z(t)$. Ein Vergleich der beiden Bilder zeigt, dass tatsächlich $z(t) = {\rm j} \cdot y(t)$ ist.
Darstellung der harmonischen Schwingung als analytisches Signal
Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi f_{\rm T} \cdot t - \varphi)$ besteht bekanntlich aus zwei Diracfunktionen bei den Frequenzen
- $+f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$,
- $-f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$.
Somit lautet das Spektrum des analytischen Signals (also ohne die Diracfunktion bei der Frequenz $f =-f_{\rm T}$, aber Verdoppelung bei $f =+f_{\rm T}$):
- $$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm T}) .$$
Die dazugehörige Zeitfunktion erhält man durch Anwendung des Verschiebungssatzes:
- $$x_+(t) = A \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_{\rm T} = 2\pi f_{\rm T}$ drehenden Zeiger.
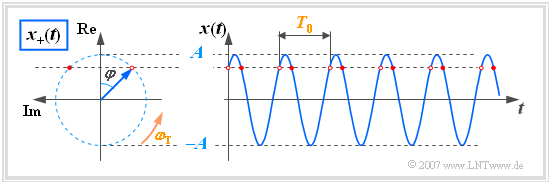
$\text{Beispiel 2:}$ Aus Darstellungsgründen wird das Koordinatensystem entgegen der üblichen Darstellung um $90^\circ$ gedreht (Realteil nach oben, Imaginärteil nach links).
Anhand dieser Grafik sind folgende Aussagen möglich:
- Zum Startzeitpunkt $t = 0$ liegt der Zeiger der Länge $A$ (Signalamplitude) mit dem Winkel $-\varphi$ in der komplexen Ebene. Im gezeichneten Beispiel gilt $\varphi = 45^\circ$.
- Für Zeiten $t > 0$ dreht der Zeiger mit konstanter Winkelgeschwindigkeit (Kreisfrequenz) $\omega_{\rm T}$ in mathematisch positiver Richtung, das heißt entgegen dem Uhrzeigersinn.
- Die Spitze des Zeigers liegt somit stets auf einem Kreis mit Radius $A$ und benötigt für eine Umdrehung genau die Zeit $T_0$, also die Periodendauer der harmonischen Schwingung $x(t)$.
- Die Projektion des analytischen Signals $x_+(t)$ auf die reelle Achse, durch rote Punkte markiert, liefert die Augenblickswerte von $x(t)$.
$x_+(t)$–Darstellung einer Summe aus drei harmonischen Schwingungen
In unserem Applet setzen wir stets einen Zeigerverbund aus drei Drehzeigern voraus. Das physikalische Signal lautet:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
- Jede der drei harmonischen Schwingungen harmonischen Schwingungen $x_{\rm T}(t)$, $x_{\rm U}(t)$ und $x_{\rm O}(t)$ wird durch eine Amplitude $(A)$, eine Frequenz $(f)$ und einen Phasenwert $(\varphi)$ charakterisiert.
- Die Indizes sind an das Modulationsverfahren Zweiseitenband–Amplitudenmodulation angelehnt. „T” steht für „Träger”, „U” für „Unteres Seitenband” und „O” für „Oberes Seitenband”. Entsprechend gilt stets $f_{\rm U} < f_{\rm T}$ und $f_{\rm O} > f_{\rm T}$. Für die Amplituden und Phasen gibt es keine Einschränkungen.
Das dazugehörige analytische Signal lautet:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
$\text{Beispiel 3:}$ Die hier angegebene Konstellation ergibt sich zum Beispiel bei der Zweiseitenband-Amplitudenmodulation des Nachrichtensignals $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ mit dem Trägersignal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. Hierauf wird in der Versuchsdurchführung häufiger eingegangen.
Bei dieser Betrachtungsweise gibt es einige Einschränkungen bezüglich der Programmparameter:
- Für die Frequenzen gelte stets $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und $f_{\rm U} = f_{\rm T} - f_{\rm N}$.
- Ohne Verzerrungen sind die Amplitude der Seitenbänder $A_{\rm O}= A_{\rm O}= A_{\rm N}/2$.
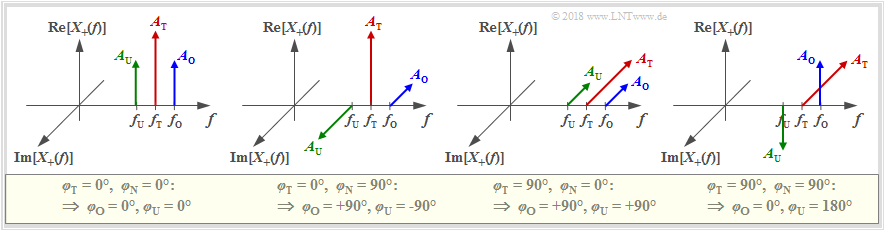
- Die jeweiligen Phasenverhältnisse können der nachfolgenden Grafik entnommen werden.
Exercises
- First select the task number.
- A task description is displayed.
- Parameter values are adjusted.
- Solution after pressing „Hide solition”.
The number „0” will reset to the same setting as the program start and will output a text with further explanation of the applet.
In the following, $\rm Green$ denotes the lower sideband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$,
$\rm Red$ the carrier ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ and
$\rm Blue$ the upper sideband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$.
(1) Consider and interpret the analytic signal $x_+(t)$ for $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1.5\ \text{V}, \ f_{\rm T} = 50 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$. In addition, $A_{\rm U} = A_{\rm O} = 0$.
- Which Signal values $x_+(t)$ result for $t = 0$, $t = 5 \ \rm µ s$ and $t = 20 \ \rm µ s$? How lange are the corresponding signal values of $x(t)$?
- For a cosine signal $x_+(t= 0) = A_{\rm T} = 1.5\ \text{V}$. Then $x_+(t)$ rotates in a mathematically positive direction (one revolution per period $T_0 = 1/f_{\rm T}$):
- $x_+(t= 20 \ {\rm µ s}) = x_+(t= 0) = 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 20 \ {\rm µ s}) = 1.5\ \text{V,}\hspace{0.5cm} x_+(t= 5 \ {\rm µ s}) = {\rm j} \cdot 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 5 \ {\rm µ s}) = {\rm Re}[x_+(t= 5 \ {\rm µ s})] = 0$.
(2) How do the ratios change for $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1.0\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 90^\circ$?
- The signal $x(t)$ is now a sine signal with a smaller amplitude. The analytic signal now starts because of $\varphi_{\rm T} = 90^\circ$ ⇒ $\phi_{\rm T} = -90^\circ$ bei $x_+(t= 0) = -{\rm j} \cdot A_{\rm T}$. After that, $x_+(t)$ rotates again in a mathematically positive direction, but twice as fast because of $T_0 = 10 \ \rm µ s$ as in $\rm (1)$.
(3) Now applies $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$.
- Consider and interpret the physical signal $x(t)$ the analytic signal $x_+(t)$.
- The Signal $x(t)$ results in the double sideband–Amplitude modulation (ZSB–AM) of the message signals $A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$ with $A_{\rm N} = 0.8\ \text{V}$, $f_{\rm N} = 20\ \text{kHz}$. The carrier $x_{\rm T}(t)$ with $f_{\rm T} = 100\ \text{kHz}$ is also cosinusoidal. The degree of modulation is $m = A_{\rm N}/A_{\rm T} = 0.8$ and the period $T_{\rm 0} = 50\ \text{µs}$.
- In the phasor diagram, the (red) carrier rotates faster than the (green) lower sideband and slower than the (blue) upper sideband. The analytic signal $x_+(t)$ results as the geometric sum of the three rotating hands. It seems that the blue pointer is leading the wearer and the green pointer is following the wearer.
(4) The settings of task (3)continue to apply. Which signal values are obtained at $t=0$, $t=2.5 \ \rm µ s$, $t= 5 \ \rm µ s$ and $t=10 \ \rm µ s$?
- At time $t=0$, all the pointers are in the direction of the real axis, so that $x(t=0) = {\rm Re}\big [x+(t= 0)\big] = A_{\rm U} + A_{\rm T} + A_{\rm O} = 1.8\ \text{V}$.
- Until the time $t=2.5 \ \rm µ s$, the red carrier has rotated by $90^\circ$, the blue pointer by $108^\circ$ and the green by $72^\circ$. We have $x(t=2.5 \ \rm µ s) = {\rm Re}\big [x_+(t= 2.5 \ \rm µ s)\big] = 0$, because now the pointer group points in the direction of the imaginary axis. The other sought signal values are $x(t=5 \ \rm µ s) = {\rm Re}\big [x_+(t= 5 \ \rm µ s)\big] = -1.647\ \text{V}$ and $x(t=10 \ \rm µ s) = {\rm Re}\big [x_+(t= 10 \ \rm µ s)\big] = 1.247\ \text{V}$.
- For $x_+(t)$ a spiral shape results, alternating with a smaller radius and then with a larger radius.
(5) How should the phase parameters $\varphi_{\rm T}$, $\varphi_{\rm U}$ and $\varphi_{\rm O}$ be set if both the carrier $x_{\rm T}(t)$ and the message signal $x_{\rm N}(t)$ are sinusoidal?
- The parameter selection $\varphi_{\rm T} = \varphi_{\rm U} = \varphi_{\rm O}=90^\circ$ describes the signals $x_{\rm T}(t) = A_{\rm T}\cdot \sin\left(2\pi f_{\rm T}\cdot t\right)$ and $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$. If, in addition, the message $x_{\rm N}(t)$ is sinusoidal, then $\varphi_{\rm O}=\varphi_{\rm T} - 90^\circ = 0$ and $\varphi_{\rm U}=\varphi_{\rm T} + 90^\circ = 180^\circ$ must be set.
(6) The settings of task (3) apply except $A_{\rm T} = 0.6\ \text{V}$. Which modulation method is described here?
- What are the consequences of this? What changes with $A_{\rm T} = 0$?
- It is a ZSB–AM with carrier with the modulation degree $m=0.8/0.6 = 1.333$. For $m > 1$, however, Synchrondemodulation is required. Hüllkurvendemodulation no longer works.
- With $A_{\rm T} = 0$ ⇒ $m \to \infty$ results in a ZSB–AM without carrier. Also for this you absolutely need the synchronous demodulation.
(7) Now applies $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 90^\circ$.
- Which constellation is described here? What changes with $A_{\rm U} = 0.8\ \text{V}$ und $A_{\rm O} = 0$?
- In both cases, it is a Einseitenbandmodulation (ESB–AM) with the modulation degree $\mu = 0.8$ (in ESB we denote the degree of modulation with $\mu$ instead $m$). he carrier signal is cosinusoidal and the message signal is sinusoidal.
- $A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ is an OSB modulation. The green pointer is missing and the blue pointer rotates faster compared to the red carrier.
- $A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ is a USB modulation. The blue pointer is missing and the green pointer rotates slower compared to the red carrier.
(8) Now applies $\text{Red:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blue:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$.
- Which constellation could be described here? Which figure is given for the equivalent lowpass–signal $x_{\rm TP}(t)$? ⇒ „locus”?
- It could be a ZSB–AM of a sinusoidal signal with cosinusoidal carrier and modulation degree $m=0.8$, in which the upper sideband is attenuated by a factor of 2. The equivalent lowpass–signal $x_{\rm TP}(t)$ has an elliptical course in the complex plane.
Applet Manual
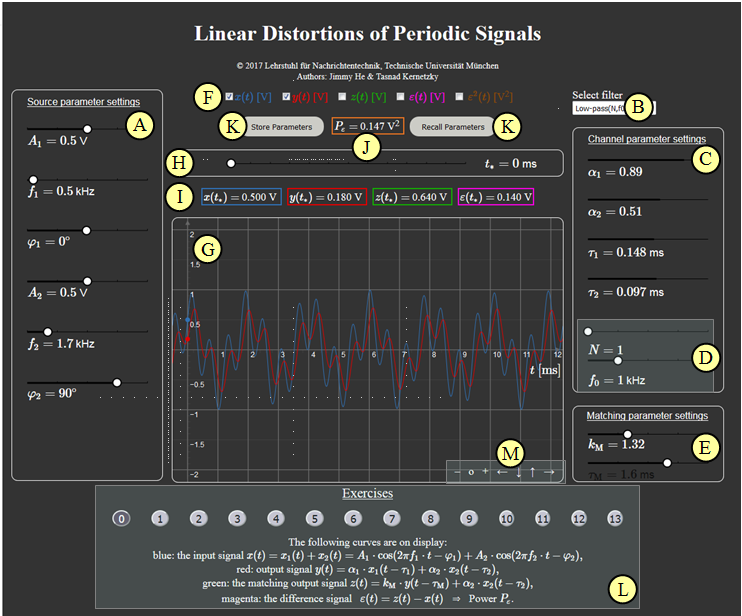
(A) Parametereingabe für das Eingangssignal $x(t)$ per Slider: Amplituden, Frequenzen, Phasenwerte
(B) Vorauswahl für die Kanalparameter: per Slider, Tiefpass oder Hochpass
(C) Eingabe der Kanalparameter per Slider: Dämpfungsfaktoren und Phasenlaufzeiten
(D) Eingabe der Kanalparameter für Hoch– und Tiefpass: Ordnung $n$, Grenzfrequenz $f_0$
(E) Eingabe der Matching–Parameter $k_{\rm M}$ und $\varphi_{\rm M}$
(F) Auswahl der darzustellenden Signale: $x(t)$, $y(t)$, $z(t)$, $\varepsilon(t)$, $\varepsilon^2(t)$
(G) Graphische Darstellung der Signale
(H) Eingabe der Zeit $t_*$ für die Numerikausgabe
( I ) Numerikausgabe der Signalwerte $x(t_*)$, $y(t_*)$, $z(t_*)$ und $\varepsilon(t_*)$
(J) Numerikausgabe des Hauptergebnisses $P_\varepsilon$
(K) Abspeichern und Zurückholen von Parametersätzen
(L) Bereich für die Versuchsdurchführung: Aufgabenauswahl, Aufgabenstellung und Musterlösung
(M) Variationsmöglichkeiten für die grafische Darstellung
$\hspace{1.5cm}$Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
$\hspace{1.5cm}$Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
$\hspace{1.5cm}$Andere Möglichkeiten:
$\hspace{1.5cm}$Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
$\hspace{1.5cm}$Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
About the Authors
This interactive calculation was designed and realized at the Lehrstuhl für Nachrichtentechnik of the Technischen Universität München .
- The original version was created in 2005 by Ji Li as part of her Diploma thesis using „FlashMX–Actionscript” (Supervisor: Günter Söder).
- In 2018 this Applet was redesigned and updated to „HTML5” by Xiaohan Liu as part of her Bachelor's thesis (Supervisor: Tasnád Kernetzky).