Aufgaben:Exercise 2.11Z: Arithmetic Coding once again

• Return to book

Vorgegebene Intervallbereiche

Wir betrachten hier die arithmetische Codierung (AC). Alle notwendigen Informationen zu dieser Art von Entropiecodierung finden Sie in der Aufgabe 2.11.

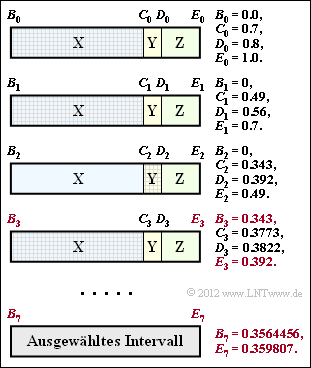
Auch die Grafik ist das Ergebnis von Aufgabe 2.11. Die für die aktuelle Aufgabe wichtigen Zahlenwerte für die Codierschritte 3 und 7 sind farblich hervorgehoben:

• Das Intervall für $N= 3$ (Symbolfolge $\rm XXY$) beginnt bei $B_3 = 0.343$ und reicht bis zum Endwert $E_3 = 0.392$.
• Das Intervall für $N= 7$ (Symbolfolge $\rm XXYXXXZ$) wird durch $B_7 = 0.3564456$ und $E_7 =0.359807$ begrenzt.

In dieser Aufgabe geht es nur um die Zuweisung von Binärfolgen zu den ausgewählten Intervallen. Vorgehensweise:

• Das Intervall $I$ wird bestimmt durch den Beginn $B$, das Ende $E$, die Intervallbreite ${\it \Delta} = E-B$ sowie die Intervallmitte  $M = (B+E)/2$.
• Das Intervall $I$ wird gekennzeichnet durch die Binärdarstellung (mit begrenzter Auflösung) eines beliebigen reellen Zahlenwertes $r \in I$ . Beispielsweise wählt man  $r \approx M$.
• Die erforderliche Bitanzahl ergibt sich aus der Intervallbreite nach folgender Gleichung (die nach unten offenen Klammern bedeuten „nach oben runden”):

$$N_{\rm Bit} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$

Beispielsweise steht für $N_{\rm Bit} = 5$ der Binärcode 01001 für die folgende reellwertige Zahl r:

$$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 \hspace{0.05cm}. $$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Weitere Quellencodierverfahren.
• Insbesondere wird Bezug genommen auf die Seite  Arithmetische Codierung.
• Weitere Informationen zum Thema finden Sie auch in diesem  WIKIPEDIA-Artikel

Fragebogen

1

Wie viele Bit werden zur Darstellung der Quellensymbolfolge $\rm XXY$   ⇒   $N = 3$ benutzt?

$N_\text{Bit} \ = \ $

2

Welcher arithmetischer Code (AC) gilt für diesen Fall?

	AC = 01011,
	AC = 010111,
	AC = 110111.

3

Wie viele Bit werden zur Darstellung der Quellensymbolfolge $\rm XXYXXXZ$   ⇒   $N = 7$ benutzt?

$N_\text{Bit} \ = \ $

4

Ist 01011100001 ein gültiger Code für die Quellensymbolfolge $\rm XXYXXXZ$?

	Ja.
	Nein.

5

Welche Aussagen gelten für die arithmetische Codierung allgemein?

	Es handelt sich um eine gemeinsame Codierung ganzer Folgen.
	Eine 32 Bit–Rechnerarchitektur begrenzt die Folgenlänge $N$.
	Dieses Problem lässt sich durch Integer–Realisierung umgehen.
	Eine Integer–Realisierung erhöht die Codiergeschwindigkeit.

Musterlösung

Solution

(1)  Das ausgewählte Intervall beginnt bei $B_3 = 0.343$ und endet bei $E_3 = 0.392$. Die Intervallbreite ist somit Δ₃ = 0.049 und damit gilt mit dem Logarithmus dualis:

$$N_{\rm Bit} = {\rm log_2} \hspace{0.15cm} \left\lceil \frac{1}{0.049}\right\rceil+1\hspace{0.15cm}\underline{= 6} \hspace{0.05cm}.$$

(2)  Das ausgewählte Intervall ergibt sich zu $I = \big[0.343, 0.392\big)$.

• Die Mitte liegt bei $M_3 = 0.3675$.
• Zur Bestimmung des arithmetischen Codes versuchen wir, die Intervallmitte durch eine Binärdarstellung möglichst gut zu erreichen.
• Da uns gerade kein entsprechendes Tool zur Lösung dieser Aufgabe zur Verfügung steht, gehen wir von folgenden Nebenrechnungen aus:

 $H_4 = 2^{-2} + 2^{-2} = 0.3125$   ⇒   gehört nicht zum Intervall $I$.

 $H_5 = H_4 +2^{-5} = 0.34375 \in I$   ⇒   Binärdarstellung: 0.01011  ⇒  Code:   01011.

 $H_6 = H_5 +2^{-6} = 0.359375 \in I$   ⇒   Binärdarstellung: 0.010111  ⇒  Code:   010111.

 $H_7 = H_6 +2^{-7} = 0.3671875 \in I$   ⇒   Binärdarstellung: 0.0101111  ⇒  Code:   0101111.

 $H_{12} = H_7 +2^{-12} = 0.3674316406 \in I$   ⇒   Binärdarstellung: 0.010111100001  ⇒  Code:   010111100001.

Der entsprechende 6 Bit–Code lautet somit AC = 010111   ⇒   Richtig ist der Lösungsvorschlag 2.

(3)  Hier ergibt sich mit dem Beginn $B_7 = 0.3564456$ und dem Ende $E_7 = 0.359807$ die Intervallbreite $\Delta_7 = 0.0033614$ und damit

$$N_{\rm Bit} = \left\lceil {\rm log_2} \hspace{0.15cm} \frac{1}{0.0033614} \right\rceil + 1\hspace{0.15cm} = \left\lceil {\rm log_2} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} \hspace{0.05cm}.$$

(4)  Die Binärdarstellung des Codes 01011100001 ergibt

$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 \hspace{0.05cm}.$$

Richtig ist also NEIN. Der gültige arithmetische Code ist AC = 01011011101, wegen

$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7.$$

(5)  Alle Aussagen sind richtig. Siehe auch:

Bodden, E.; Clasen, M.; Kneis, J.: Algebraische Kodierung. Proseminar, Lehrstuhl für Informatik IV, RWTH Aachen, 2002.