Difference between revisions of "Aufgaben:Exercise 3.8: Once more Mutual Information"
| Line 4: | Line 4: | ||
[[File:P_ID2768__Inf_A_3_7_neu.png|right|frame|„Wahrscheinlichkeiten” $P_{ XY }$ und $P_{ XW }$]] | [[File:P_ID2768__Inf_A_3_7_neu.png|right|frame|„Wahrscheinlichkeiten” $P_{ XY }$ und $P_{ XW }$]] | ||
| − | Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen: | + | Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen: |
| − | :$$X = \{ 0 , 1 , 2 \} , \hspace{0.3cm}Y= \{ 0 , 1 , 2 \}.$$ | + | :$$X = \{ 0 ,\ 1 ,\ 2 \} , \hspace{0.3cm}Y= \{ 0 ,\ 1 ,\ 2 \}.$$ |
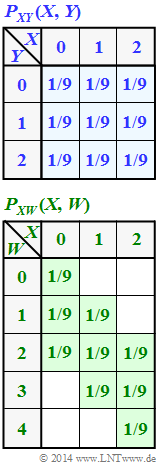
| − | Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ beider Zufallsgrößen ist in der oberen Grafik angegeben. In der [[Aufgaben:3.07Z_Tupel_aus_tern%C3%A4ren_Zufallsgr%C3%B6%C3%9Fen|Aufgabe 3.8Z]] wird diese Konstellation ausführlich analysiert. Man erhält als Ergebnis (alle Angaben in „bit”): | + | Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ beider Zufallsgrößen ist in der oberen Grafik angegeben. |
| + | |||
| + | In der [[Aufgaben:3.07Z_Tupel_aus_tern%C3%A4ren_Zufallsgr%C3%B6%C3%9Fen|Aufgabe 3.8Z]] wird diese Konstellation ausführlich analysiert. Man erhält als Ergebnis (alle Angaben in „bit”): | ||
:* $H(X) = H(Y) = \log_2 (3) = 1.585,$ | :* $H(X) = H(Y) = \log_2 (3) = 1.585,$ | ||
:* $H(XY) = \log_2 (9) = 3.170,$ | :* $H(XY) = \log_2 (9) = 3.170,$ | ||
| Line 14: | Line 16: | ||
:* $I(X, Z) = 1.585.$ | :* $I(X, Z) = 1.585.$ | ||
| − | Desweiteren betrachten wir | + | Desweiteren betrachten wir die Zufallsgröße $W = \{ 0,\ 1,\ 2,\ 3,\ 4 \}$, deren Eigenschaften sich aus der Verbundwahrscheinlichkeitsfunktion $P_{ XW }(X, W)$ nach der unteren Skizze ergeben. Die Wahrscheinlichkeiten sind in allen weiß hinterlegten Feldern jeweils Null. |
Gesucht ist in der vorliegenden Aufgabe die Transinformation zwischen | Gesucht ist in der vorliegenden Aufgabe die Transinformation zwischen | ||
| − | :*den Zufallsgrößen $X$ und $W$ ⇒ $I(X; W)$, | + | :*den Zufallsgrößen $X$ und $W$ ⇒ $I(X; W)$, |
| − | :* den Zufallsgrößen $Z$ und $W | + | :* den Zufallsgrößen $Z$ und $W ⇒ I(Z; W)$. |
| Line 25: | Line 27: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|Verschiedene Entropien zweidimensionaler Zufallsgrößen]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|Verschiedene Entropien zweidimensionaler Zufallsgrößen]]. |
*Insbesondere wird Bezug genommen auf die Seiten <br> [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Bedingte_Wahrscheinlichkeit_und_bedingte_Entropie|Bedingte Wahrscheinlichkeit und bedingte Entropie]] sowie <br> [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Transinformation_zwischen_zwei_Zufallsgr.C3.B6.C3.9Fen|Transinformation zwischen zwei Zufallsgrößen]]. | *Insbesondere wird Bezug genommen auf die Seiten <br> [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Bedingte_Wahrscheinlichkeit_und_bedingte_Entropie|Bedingte Wahrscheinlichkeit und bedingte Entropie]] sowie <br> [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Transinformation_zwischen_zwei_Zufallsgr.C3.B6.C3.9Fen|Transinformation zwischen zwei Zufallsgrößen]]. | ||
| Line 33: | Line 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie könnten die Größen $X$, $Y$ und $W$ zusammenhängen? | + | {Wie könnten die Größen $X$, $Y$ und $W$ zusammenhängen? |
|type="[]"} | |type="[]"} | ||
+ $W = X + Y$, | + $W = X + Y$, | ||
| Line 39: | Line 41: | ||
-$W = Y - X + 2$. | -$W = Y - X + 2$. | ||
| − | {Welche Transinformation besteht zwischen den Zufallsgrößen $X$ und $W$? | + | {Welche Transinformation besteht zwischen den Zufallsgrößen $X$ und $W$? |
|type="{}"} | |type="{}"} | ||
$I(X; W) \ = \ $ { 0.612 3% } $\ \rm bit$ | $I(X; W) \ = \ $ { 0.612 3% } $\ \rm bit$ | ||
| − | {Welche Transinformation besteht zwischen den Zufallsgrößen $Z$ und $W$? | + | {Welche Transinformation besteht zwischen den Zufallsgrößen $Z$ und $W$? |
|type="{}"} | |type="{}"} | ||
$I(Z; W) \ = \ $ { 2.197 3% } $\ \rm bit$ | $I(Z; W) \ = \ $ { 2.197 3% } $\ \rm bit$ | ||
| Line 49: | Line 51: | ||
{Welche der nachfolgenden Aussagen sind zutreffend? | {Welche der nachfolgenden Aussagen sind zutreffend? | ||
|type="[]"} | |type="[]"} | ||
| − | + Es gilt $H(ZW) = H(XW)$. | + | + Es gilt $H(ZW) = H(XW)$. |
| − | + Es gilt $H(W|Z) = 0$. | + | + Es gilt $H(W|Z) = 0$. |
| − | + Es gilt $I(Z; W) > I(X; W)$. | + | + Es gilt $I(Z; W) > I(X; W)$. |
</quiz> | </quiz> | ||
Revision as of 14:13, 31 January 2020
Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen:
- $$X = \{ 0 ,\ 1 ,\ 2 \} , \hspace{0.3cm}Y= \{ 0 ,\ 1 ,\ 2 \}.$$
Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ beider Zufallsgrößen ist in der oberen Grafik angegeben.
In der Aufgabe 3.8Z wird diese Konstellation ausführlich analysiert. Man erhält als Ergebnis (alle Angaben in „bit”):
- $H(X) = H(Y) = \log_2 (3) = 1.585,$
- $H(XY) = \log_2 (9) = 3.170,$
- $I(X, Y) = 0,$
- $H(Z) = H(XZ) = 3.170,$
- $I(X, Z) = 1.585.$
Desweiteren betrachten wir die Zufallsgröße $W = \{ 0,\ 1,\ 2,\ 3,\ 4 \}$, deren Eigenschaften sich aus der Verbundwahrscheinlichkeitsfunktion $P_{ XW }(X, W)$ nach der unteren Skizze ergeben. Die Wahrscheinlichkeiten sind in allen weiß hinterlegten Feldern jeweils Null.
Gesucht ist in der vorliegenden Aufgabe die Transinformation zwischen
- den Zufallsgrößen $X$ und $W$ ⇒ $I(X; W)$,
- den Zufallsgrößen $Z$ und $W ⇒ I(Z; W)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Verschiedene Entropien zweidimensionaler Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seiten
Bedingte Wahrscheinlichkeit und bedingte Entropie sowie
Transinformation zwischen zwei Zufallsgrößen.
Fragebogen
Musterlösung
- Mit $X = \{0, 1, 2\}$, $Y = \{0, 1, 2\}$ gilt $X + Y = \{0, 1, 2, 3, 4\}$. Auch die Wahrscheinlichkeiten stimmen mit der gegebenen Wahrscheinlichkeitsfunktion überein.
- Die Überprüfung der beiden anderen Vorgaben zeigt, dass auch $W = X – Y + 2$ möglich ist, nicht jedoch $W = Y – X + 2$.
(2) Aus der 2D–Wahrscheinlichkeitsfunktion $P_{ XW }(X, W)$ auf der Angabenseite erhält man für
- die Verbundentropie:
- $$H(XW) = {\rm log}_2 \hspace{0.1cm} (9) = 3.170\,{\rm (bit)} \hspace{0.05cm},$$
- die Wahrsacheinlichkeitsfunktion der Zufallsgröße $W$:
- $$P_W(W) = \big [\hspace{0.05cm}1/9\hspace{0.05cm}, \hspace{0.05cm} 2/9\hspace{0.05cm},\hspace{0.05cm} 3/9 \hspace{0.05cm}, \hspace{0.05cm} 2/9\hspace{0.05cm}, \hspace{0.05cm} 1/9\hspace{0.05cm} \big ]\hspace{0.05cm},$$
- die Entropie der Zufallsgröße $W$:
- $$H(W) = 2 \cdot \frac{1}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{1} + 2 \cdot \frac{2}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{2} + \frac{3}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{3} {= 2.197\,{\rm (bit)}} \hspace{0.05cm}.$$
Mit $H(X) = 1.585 \ \rm bit$ (wurde vorgegeben) ergibt sich somit für die Mutual Information:
- $$I(X;W) = H(X) + H(W) - H(XW) = 1.585 + 2.197- 3.170\hspace{0.15cm} \underline {= 0.612\,{\rm (bit)}} \hspace{0.05cm}.$$
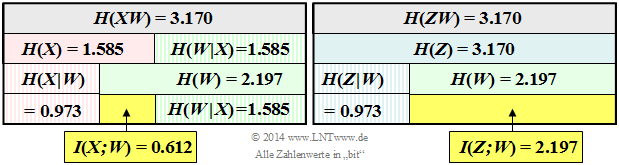
Das linke Schaubild verdeutlicht die Berechnung der Transinformation $I(X; W)$ zwischen der ersten Komponente $X$ und der Summe $W$.
(3) Die zweite Grafik zeigt die Verbundwahrscheinlichkeit $P_{ ZW }(⋅)$. Das Schema besteht aus $5 · 9 = 45$ Feldern im Gegensatz zur Darstellung von $P_{ XW }(⋅)$ auf der Angabenseite mit $3 · 9 = 27$ Feldern.
- Von den $45$ Feldern sind aber auch nur neun mit Wahrscheinlichkeiten ungleich $0$ belegt. Für die Verbundentropie gilt: $H(ZW) = 3.170\,{\rm (bit)} \hspace{0.05cm}.$
- Mit den weiteren Entropien $H(Z) = 3.170\,{\rm (bit)}\hspace{0.05cm}$ und $H(W) = 2.197\,{\rm (bit)}\hspace{0.05cm}$ entsprechend der Aufgabe 3.8Z bzw. der Teilfrage (2) dieser Aufgabe erhält man für die Transinformation:
- $$I(Z;W) = H(Z) + H(W) - H(ZW) \hspace{0.15cm} \underline {= 2.197\,{\rm (bit)}} \hspace{0.05cm}.$$
(4) Alle drei Aussagen treffen zu, wie auch aus dem oberen Schaubild ersichtlich ist. Wir versuchen eine Interpretation dieser numerischen Ergebnisse:
- Die Verbundwahrscheinlichkeit $P_{ ZW }(⋅)$ setzt sich ebenso wie $P_{ XW }(⋅)$ aus neun gleichwahrscheinlichen Elementenungleich 0 zusammen. Damit ist offensichtlich, dass auch die Verbundentropien gleich sind ⇒ $H(ZW) = H(XW) = 3.170 \ \rm (bit)$.
- Wenn ich das Tupel $Z = (X, Y)$ kenne, kenne ich natürlich auch die Summe $W = X + Y$. Damit ist $H(W|Z) = 0$.
- Dagegen ist $H(Z|W) \ne 0$. Vielmehr gilt $H(Z|W) = H(X|W) = 0.973 \ \rm (bit)$.
- Die Zufallsgröße $W$ liefert also die genau gleiche Information hinsichtlich des Tupels $Z$ wie für die Einzelkomponente $X$. Dies ist die verbale Interpretation der Aussage $H(Z|W) = H(X|W)$.
- Die gemeinsame Information von $Z$ und $W$ ⇒ $I(Z; W)$ ist größer als die gemeinsame Information von $X$ und $W$ ⇒ $I(X; W)$ , weil $H(W|Z) =0$ gilt, während $H(W|X)$ ungleich $0$ ist, nämlich genau so groß ist wie $H(X)$ :
- $$I(Z;W) = H(W) - H(W|Z) = 2.197 - 0= 2.197\,{\rm (bit)} \hspace{0.05cm},$$
- $$I(X;W) = H(W) - H(W|X) = 2.197 - 1.585= 0.612\,{\rm (bit)} \hspace{0.05cm}.$$