Aufgaben:Exercise 4.11Z: Error Probability with QAM

• Return to book

Tabelle zweier unterschiedlicher Gaußscher Fehlerfunktionen

Wir gehen von den folgenden Voraussetzungen aus:

• binäre bipolare Amplitudenkoeffizienten  $a_ν ∈ \{±1\}$,
• rechteckförmiger Sendegrundimpuls mit Amplitude  $s_0$  und Bitdauer  $T_{\rm B}$,
• AWGN–Rauschen mit der Rauschleistungsdichte  $N_0$,
• Empfänger gemäß dem Matched–Filter–Prinzip,
• bestmögliche Demodulation und Detektion.

Wie schon mehrfach gezeigt wurde, kann man die Bitfehlerwahrscheinlichkeit der binären Phasenmodulation (BPSK) bei diesen Randbedingungen mit den folgenden Gleichungen berechnen:

$$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$

$$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$

Die entsprechenden Gleichungen der 4–QAM lauten:

$$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$

Hierbei ist berücksichtigt, dass man – um die gleiche Sendeenergie pro Bit wie bei der BPSK zu erreichen – die Impulsamplitude  $g_0$  der Rechteckimpulse in den beiden Teilzweigen der 4–QAM um den Faktor  $\sqrt{2}$  herabsetzen muss. Die Hüllkurve ist dann bei beiden Systemen gleich  $s_0$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Quadratur–Amplitudenmodulation.
• Bezug genommen wird aber auch auf die Seite  Fehlerwahrscheinlichkeiten – ein kurzer Überblick  im vorherigen Kapitel.
• Gehen Sie stets von den folgenden Zahlenwerten aus:   $s_0 = 2\,{\rm V}, \hspace{0.05cm} N_0 = 0.25 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}.$
• Die Bitdauer beträgt  $T_{\rm B} = 1 \ \rm µ s$  (Teilaufgabe 1) bzw.  $T_{\rm B} = 2 \ \rm µ s$  (ab Teilaufgabe 2).
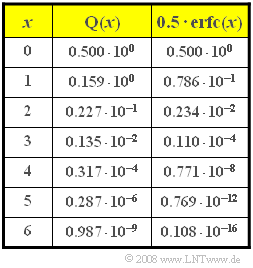
• In der Tabelle sind die beiden gebräuchlichen Gaußschen Fehlerfunktionen  ${\rm Q}(x)$  und  $1/2 \cdot {\rm erfc}(x)$  angegeben.
• Energien sind in  $\rm V^2s$  anzugeben; sie beziehen sich somit auf den Bezugswiderstand  $R = 1 \ \rm \Omega$.

Fragebogen

1

Welche Fehlerwahrscheinlichkeit  $p_\text{B, BPSK}$  ergibt sich für  Binary Phase Shift Keying  (BPSK) mit $T_{\rm B} = 1 \ \rm µ s$?

$p_\text{B, BPSK} \ = \ $ $\ \rm 10^{-4}$

2

Welche Fehlerwahrscheinlichkeit  $p_\text{B, BPSK}$  ergibt sich für   Binary Phase Shift Keying  (BPSK) mit $T_{\rm B} = 2 \ \rm µ s$?

$p_\text{B, BPSK} \ = \ $ $\ \rm 10^{-8}$

3

Welche Fehlerwahrscheinlichkeit  $p_\text{B, 4-QAM}$  erhält man für die 4–QAM mit  $E_{\rm B} = 4 · 10^{–6} \ \rm V^2s$?

$p_\text{B, 4-QAM} \ = \ $ $\ \rm 10^{-8}$

4

Was trifft zu, wenn man nur einen Zweig $\rm (I$ oder $\rm Q)$ der 4–QAM betrachtet?

	Es ergibt sich das gleiche Ergebnis wie für die gesamte 4–QAM.
	Der Abstand der Nutzabtastwerte ist wie bei der BPSK gleich  $s_0$.
	Es ergibt sich die gleiche Rauschleistung wie bei der BPSK.

Musterlösung

Solution

(1)  Mit den vorgegebenen Werten erhält man für  Binary Phase Shift Keying  (BPSK):

$$E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} = \frac{1}{2}\cdot (2\,{\rm V})^2 \cdot 1\,{\rm \mu s} = 2 \cdot 10^{-6}\,{\rm V^2s} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = \frac {2 \cdot 10^{-6}\,{\rm V^2s}}{0.25 \cdot 10^{-6}\,{\rm V^2/Hz}} = 8$$

$$ \Rightarrow \hspace{0.3cm} p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{16} \right ) = {\rm Q}\left ( 4 \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{8}\right )\hspace{0.05cm}.$$

Aufgrund der gegebenen $x$–Werte in der Tabelle ist bei dieser Teilaufgabe zweckmäßigerweise die erste Gleichung anzuwenden:

$$p_\text{B, BPSK} = {\rm Q}\left ( 4 \right ) \hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4} }\hspace{0.05cm}.$$

(2)  Bei doppelter Bitdauer ist auch die Energie doppelt so groß: $E_{\rm B} = 4 · 10^{–6} \ \rm V^2s$ ⇒ $E_B/N_0 = 16$.

• Daraus folgt:

$$p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{16}\right ) ={1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$

• Aus pragmatischen Gründen wurde hier die letzte Spalte der Tabelle benutzt.

(3)  Setzt man die für die 4–QAM gegebenen Gleichungen ineinander ein, so kommt man zum gleichen Ergebnis wie bei der BPSK:

$$p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \equiv p_\text{B, BPSK}.$$

Da sich auch die Energie pro Bit gegenüber der Teilaufgabe (2) nicht geändert hat, wird sich auch die gleiche Fehlerwahrscheinlichkeit einstellen:

$$p_{\rm B, \hspace{0.05cm}4-QAM}= {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$

(4)  Richtig ist nur der erste Lösungsvorschlag:

• Die Fehlerwahrscheinlichkeit ist natürlich in den beiden Zweigen gleich groß. Warum auch nicht?
• Das würde allerdings bei einem Phasenversatz zwischen Sender und Empfänger nicht mehr gelten.
• Der Abstand der Nutzabtastwerte von der Schwelle ist hier allerdings $g_0$ und damit um den Faktor $\sqrt{2}$ kleiner als die Hüllkurve $s_0$ der gesamten 4–QAM.
• Betrachtet man den Inphase–Zweig (oder den Quadratur–Zweig) als eine eigenständige BPSK, so ist aber auch die Rauschleistung wegen der geringeren Symbolrate nur halb so groß wie bei der BPSK. Deshalb bleibt die Fehlerwahrscheinlichkeit gleich.