Difference between revisions of "Aufgaben:Exercise 1.08: Identical Codes"
| Line 82: | Line 82: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Der vorgegebene Code $\mathcal{C}$ wird durch folgende Kenngrößen charakterisiert: | '''(1)''' Der vorgegebene Code $\mathcal{C}$ wird durch folgende Kenngrößen charakterisiert: | ||
| − | *Bitanzahl der Codeworte: $\underline{n = 6}$, | + | *Bitanzahl der Codeworte: $\underline{n = 6}$, |
| − | *Bitanzahl der Informationsworte: $\underline{k = 3}$, | + | *Bitanzahl der Informationsworte: $\underline{k = 3}$, |
| − | *Anzahl der Prüfbitgleichungen: $\underline{m = n | + | *Anzahl der Prüfbitgleichungen: $\underline{m = n - k = 3}$, |
| − | *Coderate: $R = k/n = 3/6 \Rightarrow \underline{R = 0.5}$, | + | *Coderate: $R = k/n = 3/6 \Rightarrow \underline{R = 0.5}$, |
| − | *Anzahl der Codeworte (Codeumfang): $|\mathcal{C}| = 2^k \Rightarrow \underline{|C| = 8}$, | + | *Anzahl der Codeworte (Codeumfang): $|\mathcal{C}| = 2^k \Rightarrow \underline{|C| = 8}$, |
| − | *minimale Hamming–Distanz (siehe Tabelle): $\underline{d}_{\rm min} \underline{= 3}$. | + | *minimale Hamming–Distanz (siehe Tabelle): $\underline{d}_{\rm min} \underline{= 3}$. |
| + | |||
'''(2)''' Richtig ist $\underline{\rm JA}$: | '''(2)''' Richtig ist $\underline{\rm JA}$: | ||
| − | *Nach der Singleton–Schranke gilt $d_{\rm min} ≤ n – k + 1$. Mit $n = 6$ und $k = 3$ erhält man hierfür $d_{\rm min} ≤ 4$. Es kann also durchaus ein (6, 3)–Blockcode mit größerer Minimaldistanz konstruiert werden. Wie ein solcher Code aussieht, wurde freundlicherweise nicht gefragt. | + | *Nach der Singleton–Schranke gilt $d_{\rm min} ≤ n – k + 1$. Mit $n = 6$ und $k = 3$ erhält man hierfür $d_{\rm min} ≤ 4$. |
| + | *Es kann also durchaus ein (6, 3)–Blockcode mit größerer Minimaldistanz konstruiert werden. Wie ein solcher Code aussieht, wurde freundlicherweise nicht gefragt. | ||
| Line 99: | Line 101: | ||
*alle [[Kanalcodierung/Beispiele_binärer_Blockcodes#Single_Parity.E2.80.93check_Codes|Single Parity–check Codes]] (SPC): $k = n – 1, d_{\rm min} = 2$. | *alle [[Kanalcodierung/Beispiele_binärer_Blockcodes#Single_Parity.E2.80.93check_Codes|Single Parity–check Codes]] (SPC): $k = n – 1, d_{\rm min} = 2$. | ||
| + | |||
| Line 113: | Line 116: | ||
*Dieser systematische Code beinhaltet genau die gleichen Codeworte wie die Codes $\mathcal{C}$ und $\mathcal{C}'$. | *Dieser systematische Code beinhaltet genau die gleichen Codeworte wie die Codes $\mathcal{C}$ und $\mathcal{C}'$. | ||
| + | |||
| Line 122: | Line 126: | ||
:*der Code $\mathcal{C}_{\rm sys}$ die gleichen Codeworte beinhaltet wie der vorgegebene Code ''\mathcal{C}''. | :*der Code $\mathcal{C}_{\rm sys}$ die gleichen Codeworte beinhaltet wie der vorgegebene Code ''\mathcal{C}''. | ||
| − | *Für $\underline{u} = (0, 1, 0)$ lautet somit das Codewort $(0, 1, 0, ?, ?, ?)$. Ein Vergleich mit der Codetabelle von $\mathcal{C}$ auf der Angabenseite führt | + | *Für $\underline{u} = (0, 1, 0)$ lautet somit das Codewort $(0, 1, 0, ?, ?, ?)$. Ein Vergleich mit der Codetabelle von $\mathcal{C}$ auf der Angabenseite führt zu $\underline{x}_{\rm sys} = (0, 1, 0, 1, 0, 1)$. |
| + | |||
| Line 134: | Line 139: | ||
:$${ \boldsymbol{\rm G}}_{\rm sys} = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &0 &1 &0 &1\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{\rm sys} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm G}}_{\rm sys} = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &0 &1 &0 &1\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{\rm sys} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | |||
Daraus ergeben sich Prüfgleichungen (siehe Grafik): | Daraus ergeben sich Prüfgleichungen (siehe Grafik): | ||
Revision as of 15:38, 8 May 2019
Wir betrachten einen Blockcode $\mathcal{C}$, der durch folgende Generatormatrix beschrieben wird:
- $${ \boldsymbol{\rm G}} = \begin{pmatrix} 0 &0 &1 &0 &1 &1\\ 1 &0 &0 &1 &1 &0\\ 0 &1 &1 &1 &1 &0 \end{pmatrix} \hspace{0.05cm}.$$
Die Zuordnung zwischen den Informationsworten $\underline{u}$ und den Codeworten $\underline{x}$ kann der Tabelle entnommen werden. Man erkennt, dass es sich dabei nicht um einen systematischen Code handelt.
Durch Manipulation der Generatormatrix $\boldsymbol {\rm G}$ lassen sich daraus identische Codes konstruieren. Darunter versteht man Codes mit gleichen Codeworten, jedoch unterschiedlicher Zuordnung $\underline{u} \rightarrow \underline{x}$.
Folgende Operationen sind erlaubt, um einen identischen Code zu erhalten:
- Vertauschen oder Permutieren der Zeilen,
- Multiplizieren aller Zeilen mit einem konstanten Vektor ungleich $0$,
- Ersetzen einer Zeile durch eine Linearkombination zwischen dieser Zeile und einer anderen.
Für den in der Teilaufgabe (3) gesuchten Code $\mathcal{C}_{\rm sys}$ mit Generatormatrix $\boldsymbol{\rm G}_{\rm sys}$ wird weiter gefordert, dass er systematisch ist.
Hinweise :
- Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung linearer Blockcodes.
- Bezug genommen wird insbesondere auf die Seite Systematische Codes.
- Bezug genommen wird zudem auf die so genannte Singleton–Schranke. Diese besagt, dass die minimale Hamming–Distanz eines $(n, k)$–Blockcodes nach oben beschränkt ist: $d_{\rm min} \le n - k +1.$
Fragebogen
Musterlösung
- Bitanzahl der Codeworte: $\underline{n = 6}$,
- Bitanzahl der Informationsworte: $\underline{k = 3}$,
- Anzahl der Prüfbitgleichungen: $\underline{m = n - k = 3}$,
- Coderate: $R = k/n = 3/6 \Rightarrow \underline{R = 0.5}$,
- Anzahl der Codeworte (Codeumfang): $|\mathcal{C}| = 2^k \Rightarrow \underline{|C| = 8}$,
- minimale Hamming–Distanz (siehe Tabelle): $\underline{d}_{\rm min} \underline{= 3}$.
(2) Richtig ist $\underline{\rm JA}$:
- Nach der Singleton–Schranke gilt $d_{\rm min} ≤ n – k + 1$. Mit $n = 6$ und $k = 3$ erhält man hierfür $d_{\rm min} ≤ 4$.
- Es kann also durchaus ein (6, 3)–Blockcode mit größerer Minimaldistanz konstruiert werden. Wie ein solcher Code aussieht, wurde freundlicherweise nicht gefragt.
Die Minimaldistanz aller Hamming–Codes ist $d_{\rm min} = 3$, und nur der Sonderfall mit $n = 3$ und $k = 1$ erreicht den Grenzwert. Dagegen erreichen das Maximum entsprechend der Singleton–Schranke:
- alle Wiederholungscodes (Repetition Codes, RC) wegen $k = 1$und $d_{\rm min} = n$; hierzu gehört auch der (3, 1)–Hamming–Code, der ja bekannterweise identisch ist mit RC (3, 1),
- alle Single Parity–check Codes (SPC): $k = n – 1, d_{\rm min} = 2$.
(3) Richtig sind die Lösungsvorschläge 2 und 3:
- Vertauscht man Zeilen in der Generatormatrix $\boldsymbol {\rm G}$, so kommt man zu einem identischen Code $\mathcal{C}'$. Das heißt: Die Codes $\mathcal{C}$ und $\mathcal{C}'$ beinhalten die genau gleichen Codeworte.
- Beispielsweise erhält man nach zyklischem Zeilentausch $2 \rightarrow 1, 3 \rightarrow 2$ und $1 \rightarrow 3$ die neue Matrix
- $${ \boldsymbol{\rm G}}' = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &1 &1 &1 &0\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$
- Die erste und die letzte Zeile der neuen Matrix entsprechen schon den Vorgaben eines systematischen Codes, nämlich, dass deren Generatormatrix ${ \boldsymbol{\rm G}_{\rm sys}}$ mit einer Diagonalmatrix beginnen muss.
- Ersetzt man die Zeile 2 durch die Modulo–2–Summe von Zeile 2 und 3, so erhält man:
- $${ \boldsymbol{\rm G}}_{\rm sys} = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &0 &1 &0 &1\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$
- Dieser systematische Code beinhaltet genau die gleichen Codeworte wie die Codes $\mathcal{C}$ und $\mathcal{C}'$.
(4) Richtig sind die Lösungsvorschläge 1 und 2:
- Wendet man die Gleichung $\underline{x}_{\rm sys} = \underline{u} \cdot \boldsymbol{\rm G}_{\rm sys}$ auf die obigen Beispiele an, so erkennt man, dass die beiden ersten Aussagen richtig sind, nicht aber die letzte.
- Ohne Rechnung kommt man zum gleichen Ergebnis, wenn man berücksichtigt, dass
- das systematische Codewort $\underline{x}_{\rm sys}$ mit $\underline{u}$ beginnen muss,
- der Code $\mathcal{C}_{\rm sys}$ die gleichen Codeworte beinhaltet wie der vorgegebene Code \mathcal{C}.
- Für $\underline{u} = (0, 1, 0)$ lautet somit das Codewort $(0, 1, 0, ?, ?, ?)$. Ein Vergleich mit der Codetabelle von $\mathcal{C}$ auf der Angabenseite führt zu $\underline{x}_{\rm sys} = (0, 1, 0, 1, 0, 1)$.
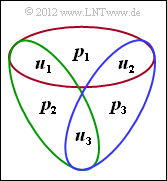
(5) Richtig ist nur die Aussage 1. Die Angaben für $p_{2}$ und $p_{3}$ sind dagegen genau vertauscht.
- Bei systematischer Codierung besteht folgender Zusammenhang zwischen Generator– und Prüfmatrix:
- $${ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_k \: ; \:{ \boldsymbol{\rm P}} \right) \hspace{0.3cm}\Leftrightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} =\left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.05cm}.$$
- Angewendet auf das aktuelle Beispiel erhält man so:
- $${ \boldsymbol{\rm G}}_{\rm sys} = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &0 &1 &0 &1\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{\rm sys} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
Daraus ergeben sich Prüfgleichungen (siehe Grafik):
- $$u_1 \oplus u_2 \oplus p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm}0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p_1 = u_1 \oplus u_2 \hspace{0.05cm},$$
- $$ u_1 \oplus u_3 \oplus p_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p_2 = u_1 \oplus u_3 \hspace{0.05cm},$$
- $$ u_2 \oplus u_3 \oplus p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p_3 = u_2 \oplus u_3 \hspace{0.05cm}.$$