Aufgaben:Exercise 3.3Z: Convolution and D-Transformation

• Return to book

Vorgegebene Filterstruktur

In dieser Aufgabe beschreiben wir an einem einfachen Beispiel

• die endliche  Impulsantwort  eines Filters:

$$\underline{g} = \left (g_0, g_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_l, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_m \right ) \hspace{0.05cm},\hspace{0.2cm}g_l \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm},$$

• die  Eingangssequenz  des Filters:

$$\underline{u} = \left (u_0, u_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, u_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) \hspace{0.05cm},\hspace{0.2cm}u_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm},$$

• die  Ausgangssequenz  des Filters:

$$\underline{x} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) \hspace{0.05cm},\hspace{0.2cm}x_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}.$$

Die Nomenklatur für diese (digitale) Filterbeschreibung haben wir an das Buch „Einführung in die Kanalcodierung” angepasst. In anderen  $\rm LNTwww$–Büchern bezeichnet oft  $\underline{x}$  den Filtereingang,  $\underline{y}$  den Filterausgang, und die Impulsantwort wird  $h$  genannt.

Allgemein gilt für die Ausgangssequenz entsprechend der  Faltung  (englisch:  Convolution ):

$$\underline{x} = \underline{u}* \underline{g} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right )\hspace{0.05cm},\hspace{0.1cm} {\rm mit} \hspace{0.2cm} x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l}\hspace{0.05cm}.$$

Wir repräsentieren nun die Zeitfunktionen  $\underline{g}, \ \underline{u}$  und  $\underline{x}$  durch Polynome in einer Dummy–Variablen  $D$  und nennen diese die  $D$–Transformierten:

$$\underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {G}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{l = 0}^{m} g_l \cdot D\hspace{0.03cm}^l = g_0 + g_1 \cdot D + g_2 \cdot D^2 + \text{...} + g_m \cdot D\hspace{0.03cm}^m\hspace{0.05cm},$$

$$\underline{u} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {U}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} u_i \cdot D\hspace{0.03cm}^i = u_0 + u_1 \cdot D + u_2 \cdot D^2 + \text{...} \hspace{0.05cm},$$

$$\underline{x} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \text{...} \hspace{0.05cm}.$$

Damit wird aus der (komplizierteren) Faltung eine Multiplikation:

$$\underline{x} = \underline{u}* \underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {X}(D) = U(D) \cdot G(D) \hspace{0.05cm}.$$

Formal lässt sich dieser Zusammenhang wie folgt nachweisen:

$${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = \sum_{i = 0}^{\infty} \sum_{l = 0}^{m}\hspace{0.1cm} g_l \cdot u_{i-l} \cdot D\hspace{0.03cm}^{i} = \sum_{l = 0}^{m} \hspace{0.1cm} g_l \cdot \sum_{j = -l}^{\infty} \hspace{0.1cm} u_{j} \cdot D\hspace{0.03cm}^{j+l} = \sum_{l = 0}^{m} \hspace{0.1cm} g_l \cdot D\hspace{0.03cm}^l \hspace{0.1cm} \cdot \hspace{0.1cm} \sum_{j = 0}^{\infty} \hspace{0.1cm} u_{j} \cdot D\hspace{0.03cm}^{j}$$

$$\Rightarrow \hspace{0.3cm}{X}(D) = U(D) \cdot G(D) \hspace{0.05cm}.$$

Hierbei wurde berücksichtigt, dass alle  $u_j$  für  $j < 0$  nicht existieren und zu Null gesetzt werden können.

Beide Vorgehensweisen zur Berechnung der Ausgangssequenz  $\underline{x}$, nämlich

• über die Faltung
• mit Hilfe der $D$–Transformation,

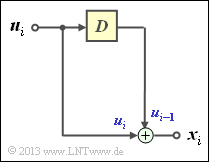
sollen für das oben skizzierte Digitale Filter demonstriert werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Algebraische und polynomische Beschreibung.
• Bezug genommen wird insbesondere auf die Seite  GF(2)–Beschreibungsformen eines Digitalen Filters.
• Berücksichtigen Sie bei der Lösung die folgende Identität für Berechnungen in  $\rm GF(2)$:

$$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...}\hspace{0.1cm}= \frac{1}{1+D} \hspace{0.05cm}.$$

Fragebogen

1

Wie lauten die vorliegenden Filterkoeffizienten?

$g_0 \ = \ $

$g_1 \ = \ $

$g_2 \ = \ $

2

Die Sequenz  $\underline{u} = (1, \, 0, \, 0, \, 1)$  sei endlich. Wie lautet die Ausgangssequenz?

	$\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$   ⇒   „Dauer–Einsfolge”.

3

Die Sequenz  $\underline{u} = (1, \, 1, \, 1)$  sei endlich. Wie lautet die Ausgangssequenz?

	$\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$   ⇒   „Dauer–Einsfolge”.

4

Wie lautet die Ausgangssequenz für  $\underline{u} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm}.)$   ⇒   „Dauer–Einsfolge”?

	$\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0, \,\text{...}\hspace{0.05cm})$.
	$\underline{x} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$   ⇒   „Dauer–Einsfolge”.

5

Für welchen Vektor  $\underline{u}$  tritt am Ausgang die Folge  $\underline{x} = (1, \, 1, \, 1, \, 1, \ \text{...}\hspace{0.05cm})$  auf?

	$\underline{u} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$   ⇒   „Dauer–Einsfolge”
	$\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \,\text{...}\hspace{0.05cm})$   ⇒   alternierende Folge, beginnend mit $1$.
	$\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$   ⇒   alternierende Folge, beginnend mit $0$.

Musterlösung

Solution

(1)  Die beiden einzigen von $0$ verschiedenen Filterkoeffizienten sind $g_0 \ \underline{= 1}$ und $g_1 \ \underline{= 1}$.

• Daraus folgt $g_2 \ \underline{= 0}$ und für die $D$–Transformierte der Impulsantwort:

$$\underline{g} = (1\hspace{0.05cm},\hspace{0.05cm} 1) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {G}(D) = 1+ D \hspace{0.05cm}.$$

(2)  Die Impulsantwort des betrachteten Filters ist $\underline{g} = (1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.

• Für die Ausgangssequenz erhält man deshalb das Faltungsprodukt

$$\underline{x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u}* \underline{g} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} ...\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) =(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} ...\hspace{0.05cm}) \hspace{0.05cm}.$$

• Zum gleichen Ergebnis kommt man über die $D$–Transformierten $U(D) = 1 + D^3$ und $G(D) = 1 + D$:

$${X}(D) = U(D) \cdot G(D) = ( 1+D^3) \cdot (1+D) = 1 +D + D^3 +D^4 \hspace{0.05cm}.$$

• Die Rücktransformation führt wieder zum Ergebnis $\underline{x} = (1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$  ⇒  Lösungsvorschlag 3.

(3)  Hier verwenden wir sofort den Weg über die $D$–Transformierten:

$${X}(D) = ( 1+D+D^2) \cdot (1+D) = 1 +D + D +D^2 +D^2 +D^3 = 1+ D^3\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$

• Das Ergebnis entspricht dem Lösungsvorschlag 2. Die folgende Berechnung soll den Weg im Zeitbereich veranschaulichen:

$$(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm},$$

$$(0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm},$$

$$(0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$

• Da die Faltung eine lineare Operation ist, ergibt sich im Galoisfeld ${\rm GF}(2)$ aus der Summation:

$$(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{0.08cm}=\hspace{0.08cm}(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$

• Hätte man die Faltung nicht in ${\rm GF}(2)$, sondern für reelle Zahlen durchgeführt, so hätte man das Ergebnis $\underline{x} = (1, \, 2, \, 2, \, 1, \, 0, \, 0, \, \text{...})$ erhalten.

(4)  Die Musterlösung zur Teilaufgabe (3) lässt bereits vermuten, dass hier der Lösungsvorschlag 1 richtig ist.

• Der Weg über die $D$–Transformierten bestätigt dieses Ergebnis:

$$\underline{u} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {U}(D)= 1+ D + D^2+ D^3 + \text{...}\hspace{0.15cm}.$$

• Mit der für Berechnungen in ${\rm GF}(2)$ gültigen Gleichung

$$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...} \hspace{0.1cm}= \frac{1}{1+D}$$

erhält man weiter:

$${X}(D) = U(D) \cdot G(D) = \frac{1}{1+D} \cdot (1+D) = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...} \hspace{0.05cm}) \hspace{0.05cm}.$$

(5)  Der Weg über die $D$–Transformierten führt zum Lösungsvorschlag 2.

• Für diese alternierende Folge $\underline{u}$, beginnend mit 1, erhält man:

$${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot (1+D) + D^2 \cdot (1+D) + D^4 \cdot (1+D) + \text{...} = 1 + D + D^2 + D^3 + D^4 + D^5 +\hspace{0.05cm} ... \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm}.$$

• Auch bei direkter Anwendung der Faltung wie in Teilaufgabe (2) kann man dieses Ergebnis ablesen.
• Mit $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...})$ erhält man dagegen $\underline{x} = (0, \, 1, \, 1, \, 1, \, 1, \, 1, \,\text{...})$.
• Diese unterscheidet sich von der „Dauer–Einsfolge” nur im ersten Bit. Es ist dann $x_1 = 0$ statt $x_1 = 1$.