Difference between revisions of "Applets:Zur Verdeutlichung der grafischen Faltung"
| Line 48: | Line 48: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' Was ändert sich, wenn man die äquivalente Impulsdauer von $h( | + | '''(2)''' Was ändert sich, wenn man die äquivalente Impulsdauer von $h(t)$ auf $\Delta t_h= 1.5$ erhöht? }} |
::* Der maximale Ausgangswert $y_{\rm max}\approx 0.53$ tritt nun bei $t_{\rm max}\approx 1.75$ auf. Durch die ungünstigere Impulsantwort wird der Eingangsimpuls stärker verformt. | ::* Der maximale Ausgangswert $y_{\rm max}\approx 0.53$ tritt nun bei $t_{\rm max}\approx 1.75$ auf. Durch die ungünstigere Impulsantwort wird der Eingangsimpuls stärker verformt. | ||
| Line 55: | Line 55: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
'''(3)''' Wählen Sie nun den symetrischen $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ und die $\text{Impulsantwort gemäß Spalt–Tiefpass: }\Delta t_h= 1$. | '''(3)''' Wählen Sie nun den symetrischen $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ und die $\text{Impulsantwort gemäß Spalt–Tiefpass: }\Delta t_h= 1$. | ||
| − | <br> Interpretieren Sie das Faltungsergebnis. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welchen Zeiten ist $y(t)>0$? Beschreibt $h( | + | <br> Interpretieren Sie das Faltungsergebnis. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welchen Zeiten ist $y(t)>0$? Beschreibt $h(t)$ ein kausales System? }} |
::* Die Faltung zweier Rechtecke mit jeweiliger Dauer $1$ ergibt ein Dreieck mit absoluter Dauer $2$ ⇒ äquivalente Impulsdauer $\Delta t_y= 1$. | ::* Die Faltung zweier Rechtecke mit jeweiliger Dauer $1$ ergibt ein Dreieck mit absoluter Dauer $2$ ⇒ äquivalente Impulsdauer $\Delta t_y= 1$. | ||
::* $y(t)$ ist im Bereich von $-0.5$ bis $+1.5$ von Null verschieden. Impulsmaximum $y_{\rm max} = 1$ bei $t_{\rm max} = +0.5$. | ::* $y(t)$ ist im Bereich von $-0.5$ bis $+1.5$ von Null verschieden. Impulsmaximum $y_{\rm max} = 1$ bei $t_{\rm max} = +0.5$. | ||
| − | ::* $h( | + | ::* $h(t)$ beschreibt ein kausales System, da $h(t) \equiv 0$ für $t < 0$ ⇒ die „Wirkung” $y(t)$ kommt nicht vor der „Ursache” $x(t)$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' Was ändert sich, wenn man die äquivalente Impulsdauer von $h( | + | '''(4)''' Was ändert sich, wenn man die äquivalente Impulsdauer von $h(t)$ auf $\Delta t_h= 2$ erhöht? }} |
::* Die Faltung zweier unterschiedlich breiten Rechtecke ergibt ein Trapez, im vorliegenden Fall zwischen $-0.5$ und $+2.5$ ⇒ äquivalente Impulsdauer $\Delta t_y= 2$. | ::* Die Faltung zweier unterschiedlich breiten Rechtecke ergibt ein Trapez, im vorliegenden Fall zwischen $-0.5$ und $+2.5$ ⇒ äquivalente Impulsdauer $\Delta t_y= 2$. | ||
| − | ::* Das Maximum $y_{\rm max} = 0.5$ tritt im Bereich $0.5 \le t \le 1.5$ auf. Bezüglich Kausalität ändert sich nichts. | + | ::* Das Maximum $y_{\rm max} = 0.5$ tritt im Bereich $0.5 \le t \le 1.5$ auf. Bezüglich der Kausalität ändert sich nichts. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
'''(5)''' Wählen Sie nun den (unsymetrischen) $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0.5$ und die $\text{ Impulsantwort eines Tiefpasses 1. Ordnung: }\Delta t_h= 1$. | '''(5)''' Wählen Sie nun den (unsymetrischen) $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0.5$ und die $\text{ Impulsantwort eines Tiefpasses 1. Ordnung: }\Delta t_h= 1$. | ||
| − | <br> Interpretieren Sie die Ergebnisse. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welchen Zeiten ist $y(t)>0$? Beschreibt $h( | + | <br> Interpretieren Sie die Ergebnisse. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welchen Zeiten ist $y(t)>0$? Beschreibt $h(t)$ ein kausales System? }} |
| − | ::* Die Impulsantwort $h( | + | ::* Die Impulsantwort $h(t)$ hat für $t > 0$ einen exponentiell abfallenden Verlauf. Füt $t > 0$ gilt stets $y(t) > 0$, aber die Signalwerte können sehr klein werden. |
::* Das Impulsmaximum $y_{\rm max} = 0.63$ tritt bei $t_{\rm max} = +1$ auf. Für $ t < t_{\rm max}$ ist der Verlauf exponentiell ansteigend, für $ t > t_{\rm max}$ exponentiell abfallend. | ::* Das Impulsmaximum $y_{\rm max} = 0.63$ tritt bei $t_{\rm max} = +1$ auf. Für $ t < t_{\rm max}$ ist der Verlauf exponentiell ansteigend, für $ t > t_{\rm max}$ exponentiell abfallend. | ||
::* Der Tiefpass 1. Ordnung kann mit einem Widerstand und einer Kapazität realisiert werden. Jedes realisierbare System ist per se kausal. | ::* Der Tiefpass 1. Ordnung kann mit einem Widerstand und einer Kapazität realisiert werden. Jedes realisierbare System ist per se kausal. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' Wählen Sie wie in '''(3)''' die rechteckförmige Impulsantwort $\text{(Spalt–Tiefpass; }\Delta t_h= 1)$. Mit welchem | + | '''(6)''' Wählen Sie wie in '''(3)''' die rechteckförmige Impulsantwort $\text{(Spalt–Tiefpass; }\Delta t_h= 1)$. Mit welchem Eingang $x(t)$ ergibt sich das gleiche $y(t)$ wie bei '''(5)'''?}} |
| − | ::* Das Signal $y(t)$ in '''(5)''' ergab sich als Faltung zwischen dem rechteckigen Eingang $x( | + | ::* Das Signal $y(t)$ in '''(5)''' ergab sich als Faltung zwischen dem rechteckigen Eingang $x(t)$ und der Exponentialfunktion $h(t)$. |
| − | ::* | + | ::* Da die Faltungsoperation kommutativ ist, ergibt sich das gleiche Ergebnis mit der Exponentialfunktion $x(t)$ und der Rechteckfunktion $h(t)$. |
| − | ::* | + | ::* Die richtige Einstellung für das Eingangssignal $x(t)$ ist $\text{Gaußimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ . |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(7)''' | + | '''(7)''' Für den Rest dieser Versuchsdurchführung betrachten wir stets den Gauß–Tiefpass; äquivalente Dauer der Impulsantwort $h(t)$: $\Delta t_h= 1$. |
| + | <br> Analsyieren und interpretieren Sie dieses „System” im Hinblick auf Kausalität und. }} | ||
::* Die Ternärquelle ist nahezu redundanzfrei: $H \approx \log_2 \ 3 \approx 1.585$. Mit $\rm A \ \to 0$, $\rm B \ \to 10$, $\rm C \ \to 11$ ist $L_{\rm M}= 1.66 > H$. | ::* Die Ternärquelle ist nahezu redundanzfrei: $H \approx \log_2 \ 3 \approx 1.585$. Mit $\rm A \ \to 0$, $\rm B \ \to 10$, $\rm C \ \to 11$ ist $L_{\rm M}= 1.66 > H$. | ||
Revision as of 11:02, 27 June 2019
Contents
Programmbeschreibung
Dieses Applet verdeutlicht die Quellencodierverfahren nach Huffman bzw. Shannon–Fano. Diese Verfahren komprimieren redundante wertdiskrete Quellen ohne Gedächtnis mit Stufenzahl $M$, dem Symbolvorrat $\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \} = \{ \rm A, \hspace{0.1cm} B, \hspace{0.1cm}\text{ ...}\}$ und den Symbolwahrscheinlichkeiten $p_{\rm A} \hspace{0.05cm},\hspace{0.1cm} p_{\rm B} \hspace{0.05cm}, \hspace{0.05cm}\text{ ...}$ .
Ziel der Quellencodierung und insbesondere der Klasse der Entropiecodierung – zu der „Huffman” und „Shannon–Fano” gehören – ist, dass die mittlere Codewortlänge $L_{\rm M}$ des binären Codes – darstellbar durch unterschiedlich lange Folgen von Nullen und Einsen – möglichst nahe an die Quellenentropie
- $$H = \sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\mu})} = -\sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}{\rm Pr}(q_{\mu})\hspace{0.5cm}\big[\hspace{0.05cm}{\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Quellensymbol}\hspace{0.05cm}\big]$$
heranreicht. Allgemein gilt $L_{\rm M} \ge H$, wobei das Gleichheitszeichen nicht für alle Symbolwahrscheinlichkeiten erreicht werden kann.
Dargestellt werden jeweils
- das Baumdiagramm zur Herleitung des jeweiligen Binärcodes, und
- eine simulierte Quellensymbolfolge der Länge $N = 10000$ (Entropie $H\hspace{0.05cm}' \approx H)$ und die dazugehörige Codesymbolfolge der Länge $L_{\rm M}\hspace{0.05cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} N$.
Auf die Einheiten „$\rm bit/Quellensymbol$” für die Entropie und die mittlere Codewortlänge wird im Programm verzichtet.
Theoretischer Hintergrund
Der Huffman–Algorithmus
Versuchsdurchführung
- Wählen Sie zunächst die Aufgabennummer.
- Eine Aufgabenbeschreibung wird angezeigt.
- Alle Parameter sind angepasst.
- Alle Grafiken und Ergebniswerte sind aktualisiert.
- Musterlösung nach Drücken von „Hide solution”.
- Nummer „0”: Gleiche Einstellung wie beim Programmstart.
(1) Wählen Sie die Parameter gemäß Voreinstellung $\text{(Gaußimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 1; \text{ Impulsantwort gemäß Tiefpass 2. Ordnung: }\Delta t_h= 1)$.
Interpretieren Sie die dargestellten Grafiken. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welcher Zeit $t_{\rm max}$ tritt dieser auf?
- Dargestellt sind nach Umbenennung: Eingangssignal $x(\tau)$ ⇒ rote Kurve, Impulsantwort $h(\tau)$ ⇒ blaue Kurve, nach Spiegelung $h(-\tau)$ ⇒ grüne Kurve.
- Verschiebt man die grüne Kurve um $t$ nach rechts, so erhält man $h(t-\tau)$. Der Ausgangswert $y(t)$ ergibt sich durch Multiplikation und Integration bzgl. $\tau$:
- $$y (t) = \int_{ - \infty }^{ +\infty } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ t } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau .$$
- Der Ausgangsimpuls $y_{\rm max}$ ist im vorliegenden Fall unsymmetrisch; der maximale Ausgangswert $y_{\rm max}\approx 0.67$ tritt bei $t_{\rm max}\approx 1.5$ auf.
(2) Was ändert sich, wenn man die äquivalente Impulsdauer von $h(t)$ auf $\Delta t_h= 1.5$ erhöht?
- Der maximale Ausgangswert $y_{\rm max}\approx 0.53$ tritt nun bei $t_{\rm max}\approx 1.75$ auf. Durch die ungünstigere Impulsantwort wird der Eingangsimpuls stärker verformt.
- Bei einem Nachrichtenübertragungssystem hätte dies stärkere Verzerrungen (Intersymbol Interference ) zur Folge.
(3) Wählen Sie nun den symetrischen $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ und die $\text{Impulsantwort gemäß Spalt–Tiefpass: }\Delta t_h= 1$.
Interpretieren Sie das Faltungsergebnis. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welchen Zeiten ist $y(t)>0$? Beschreibt $h(t)$ ein kausales System?
- Die Faltung zweier Rechtecke mit jeweiliger Dauer $1$ ergibt ein Dreieck mit absoluter Dauer $2$ ⇒ äquivalente Impulsdauer $\Delta t_y= 1$.
- $y(t)$ ist im Bereich von $-0.5$ bis $+1.5$ von Null verschieden. Impulsmaximum $y_{\rm max} = 1$ bei $t_{\rm max} = +0.5$.
- $h(t)$ beschreibt ein kausales System, da $h(t) \equiv 0$ für $t < 0$ ⇒ die „Wirkung” $y(t)$ kommt nicht vor der „Ursache” $x(t)$.
(4) Was ändert sich, wenn man die äquivalente Impulsdauer von $h(t)$ auf $\Delta t_h= 2$ erhöht?
- Die Faltung zweier unterschiedlich breiten Rechtecke ergibt ein Trapez, im vorliegenden Fall zwischen $-0.5$ und $+2.5$ ⇒ äquivalente Impulsdauer $\Delta t_y= 2$.
- Das Maximum $y_{\rm max} = 0.5$ tritt im Bereich $0.5 \le t \le 1.5$ auf. Bezüglich der Kausalität ändert sich nichts.
(5) Wählen Sie nun den (unsymetrischen) $\text{Rechteckimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0.5$ und die $\text{ Impulsantwort eines Tiefpasses 1. Ordnung: }\Delta t_h= 1$.
Interpretieren Sie die Ergebnisse. Wie groß ist der maximale Ausgangswert $y_{\rm max}$? Zu welchen Zeiten ist $y(t)>0$? Beschreibt $h(t)$ ein kausales System?
- Die Impulsantwort $h(t)$ hat für $t > 0$ einen exponentiell abfallenden Verlauf. Füt $t > 0$ gilt stets $y(t) > 0$, aber die Signalwerte können sehr klein werden.
- Das Impulsmaximum $y_{\rm max} = 0.63$ tritt bei $t_{\rm max} = +1$ auf. Für $ t < t_{\rm max}$ ist der Verlauf exponentiell ansteigend, für $ t > t_{\rm max}$ exponentiell abfallend.
- Der Tiefpass 1. Ordnung kann mit einem Widerstand und einer Kapazität realisiert werden. Jedes realisierbare System ist per se kausal.
(6) Wählen Sie wie in (3) die rechteckförmige Impulsantwort $\text{(Spalt–Tiefpass; }\Delta t_h= 1)$. Mit welchem Eingang $x(t)$ ergibt sich das gleiche $y(t)$ wie bei (5)?
- Das Signal $y(t)$ in (5) ergab sich als Faltung zwischen dem rechteckigen Eingang $x(t)$ und der Exponentialfunktion $h(t)$.
- Da die Faltungsoperation kommutativ ist, ergibt sich das gleiche Ergebnis mit der Exponentialfunktion $x(t)$ und der Rechteckfunktion $h(t)$.
- Die richtige Einstellung für das Eingangssignal $x(t)$ ist $\text{Gaußimpuls: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ .
(7) Für den Rest dieser Versuchsdurchführung betrachten wir stets den Gauß–Tiefpass; äquivalente Dauer der Impulsantwort $h(t)$: $\Delta t_h= 1$.
Analsyieren und interpretieren Sie dieses „System” im Hinblick auf Kausalität und.
- Die Ternärquelle ist nahezu redundanzfrei: $H \approx \log_2 \ 3 \approx 1.585$. Mit $\rm A \ \to 0$, $\rm B \ \to 10$, $\rm C \ \to 11$ ist $L_{\rm M}= 1.66 > H$.
- „Günstige Wahrscheinlichkeiten” wären zum Beispiel $p_{\rm A}= 0.5, \ p_{\rm B}= p_{\rm C}= 0.25$ wie bei „Quelle 1”. Dann ist $L_{\rm M}= H = 1.5$ (bit/Quellensymbol).
(8) Wählen Sie „Huffman” und die „Quelle 5” $(M=6, \ p_{\rm A}= p_{\rm B}= 0.25, \ p_{\rm C} = p_{\rm D} = p_{\rm E} = p_{\rm F} =0.125)$. Sind dies „günstige Wahrscheinlichkeiten”?
- $\rm JA$. Alle Wahrscheinlichkeiten sind $2^{-2}$ oder $2^{-3}$ ⇒ Symbole werden mit zwei oder drei Bit dargestellt ⇒ $L_{\rm M}= H = 2.5$ (bit/Quellensymbol).
(9) Wie unterscheiden sich demgegenüber die Ergebnisse für „Quelle 6” $(M=6, \ p_{\rm A}= 0.26, \ p_{\rm B}= 0.24, \ p_{\rm C} = p_{\rm D} = 0.13, \ p_{\rm E} = p_{\rm F} =0.12)$?
- Bereits durch geringfügige Wahrscheinlichkeitsabweichungen ergeben sich ein anderer Baum und damit auch andere Symbolzuordnungen.
- $\rm A$ und $\rm B$ werden mit zwei Bit codiert, die anderen mit drei Bit. $L_{\rm M}= \big [p_{\rm A} + p_{\rm B}\big] \cdot 2 + \big [p_{\rm C} + p_{\rm D}+ p_{\E}+ p_{\F}\big] \cdot 3 = 2.5$ (bit/Quellensymbol).
- Die geänderten $p_{\rm A}$, ... verändern hier nicht die mittlere Codewortlänge, aber $H=2.499$ wird (geringfügig) kleiner ⇒ $L_{\rm M} > H$ (bit/Quellensymbol).
(10) Betrachten Sie die „Quelle 9” $(M=8, \ p_{\rm A}= 0.8, \ p_{\rm B}= p_{\rm C}= p_{\rm D}=0.02, \ p_{\rm E} = 0.01$, ... , $p_{\rm H} = 0.01)$ ⇒ $H = 0.741$ (bit/Quellensymbol). Interpretation.
- Es ergibt sich mit $L_{\rm M} = 1.28$ ein sehr viel größerer Wert als $H = 0.741$ – sowohl für „Huffman” als auch für „Shannon–Fano”.
- Beide Verfahren sind also zur Quellenkomprimierung nicht geeignet, wenn eine Symbolwahrscheinlichkeit deutlich größer ist als 50%.
(11) Die Komprimierung der „Quelle 9” $(M=8, H = 2.481)$ mit „Huffman” ergibt $L_{\rm M} = 2.58$. Welches Ergebnis liefert „Shannon–Fano”? Interpretation.
- Bei „Huffman” wird ein Symbol mit einem Bit codiert, zwei mit drei Bit, drei mit vier Bit und zwei mit fünf Bit ⇒ $L_{\rm M} = 2.58$ (bit/Quellensymbol).
- Entsprechend gilt für „Shannon–Fano”: zweimal zwei Bit, dreimal drei Bit, einmal vier Bit, zweimal fünf Bit ⇒ $L_{\rm M} = 2.61$ (bit/Quellensymbol).
- $\rm Fazit$: „Huffman” ist die optimale Entropiecodierung. „Shannon–Fano” erreicht meist das gleiche Ergebnis. $\text{Aber nicht immer!}$
Zur Handhabung des Applets
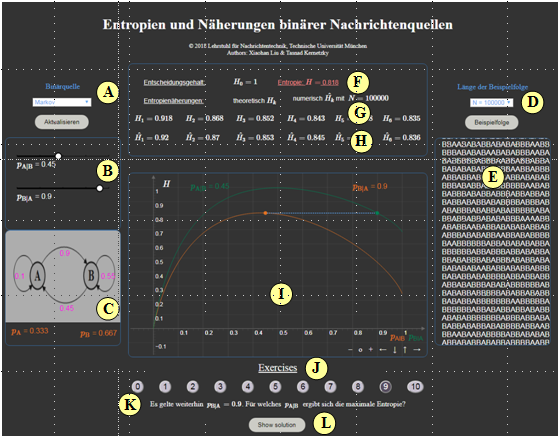
(A) Auswahl: Gedächtnislose Quelle / Markovquelle
(B) Parametereingabe per Slider (Beispiel Markovquelle)
(C) Markovdiagramm (falls Markovquelle)
(D) Eingabe der Folgenlänge $N$ zur Berechnung der $\hat H_k$
(E) Ausgabe einer simulierten Symbolfolge
(F) Ausgabe des Entropiewertes $H$
(G) Ausgabe der Entropienäherungen $H_k$
(H) Ausgabe der numerisch ermittelten Entropienäherungen $\hat H_k$
(I) Grafikfeld zur Darstellung der Funktion $H(p_{\rm A})$ bzw. $H(p_{\rm A}|p_{\rm B})$
(J) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(K) Bereich für die Versuchsdurchführung: Aufgabenstellung
(L) Bereich für die Versuchsdurchführung: Musterlösung
Über die Autoren
Dieses interaktive Applet wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2011 von Eugen Mehlmann im Rahmen seiner Bachelorarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.