Difference between revisions of "Aufgaben:Exercise 3.5: Differentiation of a Triangular Pulse"
From LNTwww
| Line 65: | Line 65: | ||
:$$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$ | :$$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$ | ||
| − | Angewandt auf das vorliegende Beispiel erhält man: | + | *Angewandt auf das vorliegende Beispiel erhält man: |
| − | :$$Y( f ) = T \cdot {\rm{j}}2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$ | + | :$$Y( f ) = T \cdot {\rm{j}}\cdot 2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$ |
| − | *Diese Funktion ist rein imaginär. Bei der Frequenz $f = 0$ verschwindet auch der Imaginärteil. Dies kann man | + | *Diese Funktion ist rein imaginär. Bei der Frequenz $f = 0$ verschwindet auch der Imaginärteil. Dies kann man zum Beispiel durch Anwendung der Regel von l'Hospital formal nachweisen ⇒ $Y( f = 0 ) \;\underline{= 0}$. |
| − | *Das Ergebnis folgt aber auch aus der Tatsache, dass der Spektralwert bei $f = 0$ gleich dem Integral über die Zeitfunktion $y(t)$ ist. | + | *Das Ergebnis folgt aber auch aus der Tatsache, dass der Spektralwert bei $f = 0$ gleich dem Integral über die Zeitfunktion $y(t)$ ist. |
| − | *Bei der normierten Frequenz $f \cdot T = 0.5$ (also für $f = 1\,\text{ kHz}$ | + | *Bei der normierten Frequenz $f \cdot T = 0.5$ $($also für $f = 1\,\text{ kHz})$ ist die Sinusfunktion gleich $1$ und man erhält $|Y(f = 1 \,\text{kHz})| = 4/\pi \cdot A \cdot T$, also näherungsweise $|Y(f=1 \ \text{kHz})| \ \underline{=0.636 \,\text{ mV/Hz}}$ (positiv imaginär). |
| − | '''(2)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u> | + | |
| − | *Die Nullstellen von $X(f)$ bleiben erhalten und es gibt eine weitere Nullstelle bei der Frequenz $f = 0$. Als asymptotischen Verlauf bezeichnet man die obere Schranke | + | '''(2)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: |
| + | *Die Nullstellen von $X(f)$ bleiben erhalten und es gibt eine weitere Nullstelle bei der Frequenz $f = 0$. | ||
| + | *Als asymptotischen Verlauf bezeichnet man die obere Schranke | ||
:$$\left| {Y_{\max }( f )} \right| = \frac{2A}{{{\rm{\pi }} \cdot |f|}} \ge \left| {Y( f )} \right|.$$ | :$$\left| {Y_{\max }( f )} \right| = \frac{2A}{{{\rm{\pi }} \cdot |f|}} \ge \left| {Y( f )} \right|.$$ | ||
| − | *Für die Frequenzen, bei denen die Sinusfunktion die Werte $\pm 1$ liefert, sind $|Y_{\text{max}}(f)|$ und $|Y(f)|$ identisch. | + | *Für die Frequenzen, bei denen die Sinusfunktion die Werte $\pm 1$ liefert, sind $|Y_{\text{max}}(f)|$ und $|Y(f)|$ identisch. |
| − | *Beim Rechteckimpuls der Amplitude $A$ lautet die entsprechende Schranke $A/(\pi \cdot |f|)$. | + | *Beim Rechteckimpuls der Amplitude $A$ lautet die entsprechende Schranke $A/(\pi \cdot |f|)$. |
| − | *Dagegen fällt das Spektrum $X(f)$ des Dreieckimpulses asymptotisch schneller ab: | + | *Dagegen fällt das Spektrum $X(f)$ des Dreieckimpulses asymptotisch schneller ab: |
:$$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$ | :$$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$ | ||
| − | *Dies ist darauf zurückzuführen, dass $x(t)$ keine Unstetigkeitsstellen aufweist. | + | *Dies ist darauf zurückzuführen, dass $x(t)$ keine Unstetigkeitsstellen aufweist. |
| − | '''(3)''' Ausgehend von einem symmetrischen Rechteckimpuls $r(t)$ mit Amplitude $A$ und Dauer $T$ kann das Signal $y(t)$ auch wie folgt dargestellt werden: | + | |
| + | '''(3)''' Ausgehend von einem symmetrischen Rechteckimpuls $r(t)$ mit Amplitude $A$ und Dauer $T$ kann das Signal $y(t)$ auch wie folgt dargestellt werden: | ||
:$$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$ | :$$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$ | ||
| − | Durch zweimalige Anwendung des Verschiebungssatzes erhält man: | + | *Durch zweimalige Anwendung des Verschiebungssatzes erhält man: |
:$$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$ | :$$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$ | ||
| − | Mit der Beziehung $\text{e}^{\text{j}x} – \text{e}^{–\text{j}x} = 2\text{j} \cdot \text{sin}(x)$ kann hierfür auch geschrieben werden: | + | *Mit der Beziehung $\text{e}^{\text{j}x} – \text{e}^{–\text{j}x} = 2\text{j} \cdot \text{sin}(x)$ kann hierfür auch geschrieben werden: |
:$$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$ | :$$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$ | ||
| − | Es ergibt sich folgerichtig das gleiche Ergebnis wie in der Teilaufgabe (1) | + | *Es ergibt sich folgerichtig das gleiche Ergebnis wie in der Teilaufgabe '''(1)'''. |
| − | |||
| − | |||
| − | Der Autor meint, dass der erste Weg etwas günstiger ist. <u>Subjektiv entscheiden wir uns für den Lösungsvorschlag 1</u>. | + | *Welcher Weg schneller zum Ergebnis führt, muss jeder selbst für sich entscheiden. Der Autor meint, dass der erste Weg etwas günstiger ist. |
| + | *<u>Subjektiv entscheiden wir uns für den Lösungsvorschlag 1</u>. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | ||
Revision as of 16:10, 26 September 2019
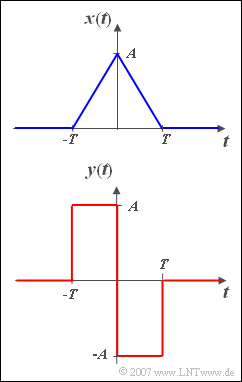
Gesucht wird das Spektrum $Y(f)$ des Signals
- $$y\left( t \right) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f \ddot{u}r}}} \\ {{\rm{f\ddot{u} r}}} \\ {{\rm{f\ddot{u}r}}} \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {{\rm{sonst}}{\rm{.}}} \\\end{array}$$
Dabei gelte $A = 1\,{\rm V}$ und $T = 0.5\,{\rm ms}$.
Als bekannt vorausgesetzt wird die Fouriertransformierte des oben skizzierten Dreieckimpulses $x(t)$, nämlich
- $$X( f ) = A \cdot T \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }}fT} ),$$
wobei $\text{si}(x) = \text{sin}(x)/x$ gilt.
Ein Vergleich der beiden Zeitsignale zeigt, dass zwischen den Funktionen $x(t)$ und $y(t)$ folgender Zusammenhang besteht:
- $$y(t) = T \cdot \frac{{{\rm d}x(t)}}{{{\rm d}t}}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
- Alle dort dargelegten Gesetzmäßigkeiten – unter Anderem auch der Verschiebungssatz und der Integrationssatz – werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.
- In der Teilaufgabe (3) soll das Spektrum $Y(f)$ ausgehend von einem symmetrischen Rechteckimpuls $r(t)$ mit Amplitude $A$ und Dauer $T$ sowie dessen Spektrum $R(f) = A \cdot T \cdot \text{si}(\pi fT)$ berechnet werden. Dies erreicht man durch zweimalige Anwendung des Verschiebungssatzes.
- In Aufgabe 3.5Z wird das Spektrum $Y(f)$ ausgehend von einem aus drei Diracfunktionen bestehenden Signal durch Anwendung des Integrationssatzes berechnet.
Fragebogen
Musterlösung
(1) Der Differentiationssatz lautet allgemein:
- $$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$
- Angewandt auf das vorliegende Beispiel erhält man:
- $$Y( f ) = T \cdot {\rm{j}}\cdot 2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$
- Diese Funktion ist rein imaginär. Bei der Frequenz $f = 0$ verschwindet auch der Imaginärteil. Dies kann man zum Beispiel durch Anwendung der Regel von l'Hospital formal nachweisen ⇒ $Y( f = 0 ) \;\underline{= 0}$.
- Das Ergebnis folgt aber auch aus der Tatsache, dass der Spektralwert bei $f = 0$ gleich dem Integral über die Zeitfunktion $y(t)$ ist.
- Bei der normierten Frequenz $f \cdot T = 0.5$ $($also für $f = 1\,\text{ kHz})$ ist die Sinusfunktion gleich $1$ und man erhält $|Y(f = 1 \,\text{kHz})| = 4/\pi \cdot A \cdot T$, also näherungsweise $|Y(f=1 \ \text{kHz})| \ \underline{=0.636 \,\text{ mV/Hz}}$ (positiv imaginär).
(2) Richtig sind die Lösungsvorschläge 1 und 3:
- Die Nullstellen von $X(f)$ bleiben erhalten und es gibt eine weitere Nullstelle bei der Frequenz $f = 0$.
- Als asymptotischen Verlauf bezeichnet man die obere Schranke
- $$\left| {Y_{\max }( f )} \right| = \frac{2A}{{{\rm{\pi }} \cdot |f|}} \ge \left| {Y( f )} \right|.$$
- Für die Frequenzen, bei denen die Sinusfunktion die Werte $\pm 1$ liefert, sind $|Y_{\text{max}}(f)|$ und $|Y(f)|$ identisch.
- Beim Rechteckimpuls der Amplitude $A$ lautet die entsprechende Schranke $A/(\pi \cdot |f|)$.
- Dagegen fällt das Spektrum $X(f)$ des Dreieckimpulses asymptotisch schneller ab:
- $$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$
- Dies ist darauf zurückzuführen, dass $x(t)$ keine Unstetigkeitsstellen aufweist.
(3) Ausgehend von einem symmetrischen Rechteckimpuls $r(t)$ mit Amplitude $A$ und Dauer $T$ kann das Signal $y(t)$ auch wie folgt dargestellt werden:
- $$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$
- Durch zweimalige Anwendung des Verschiebungssatzes erhält man:
- $$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$
- Mit der Beziehung $\text{e}^{\text{j}x} – \text{e}^{–\text{j}x} = 2\text{j} \cdot \text{sin}(x)$ kann hierfür auch geschrieben werden:
- $$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$
- Es ergibt sich folgerichtig das gleiche Ergebnis wie in der Teilaufgabe (1).
- Welcher Weg schneller zum Ergebnis führt, muss jeder selbst für sich entscheiden. Der Autor meint, dass der erste Weg etwas günstiger ist.
- Subjektiv entscheiden wir uns für den Lösungsvorschlag 1.