Aufgaben:Exercise 1.6Z: Interpretation of the Frequency Response

• Return to book

Impulsantwort und Eingangssignale

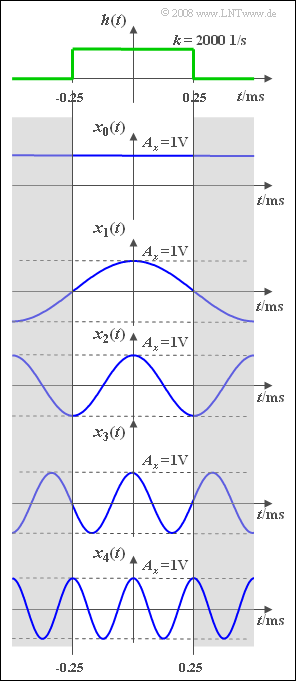
Die Aufgabe soll den Einfluss eines Tiefpasses  $H(f)$  auf cosinusförmige Signale der Form

$$x_i(t) = A_x \cdot {\rm cos}(2\pi f_i t )$$

veranschaulichen. In der Grafik sehen Sie die Signale  $x_i(t)$, wobei der Index  $i$  die Frequenz in  $\rm kHz$  angibt. So beschreibt  $x_2(t)$  ein  $2 \hspace{0.09cm} \rm kHz$–Signal.

Die Signalamplitude beträgt jeweils  $A_x = 1 \hspace{0.05cm} \rm V$. Das Gleichsignal  $x_0(t)$  ist als Grenzfall eines Cosinussignals mit der Frequenz  $f_0 =0$ zu interpretieren.

Die obere Skizze zeigt die rechteckige Impulsantwort  $h(t)$  des Tiefpasses. Dessen Frequenzgang lautet:

$$H(f) = {\rm si}(\pi {f}/{ {\rm \Delta}f}) .$$

Aufgrund der Linearität und der Tatsache, dass  $H(f)$  reell und gerade ist, sind die Ausgangssignale ebenfalls cosinusförmig:

$$y_i(t) = A_i \cdot {\rm cos}(2\pi f_i t ) .$$

• Gesucht werden die Signalamplituden  $A_i$  am Ausgang für verschiedene Frequenzen  $f_i$, wobei die Lösung ausschließlich im Zeitbereich gefunden werden soll.

• Dieser etwas umständliche Lösungsweg soll dazu dienen, den grundsätzlichen Zusammenhang zwischen Zeit– und Frequenzbereich deutlich zu machen.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Einige systemtheoretische Tiefpassfunktionen.
• Entgegen der sonst üblichen Definition der Amplitude können die „$A_i$” durchaus negativ sein. Dies entspricht dann der Funktion „Minus-Cosinus”.

Fragebogen

1

Welcher Tiefpass liegt hier vor?

	Idealer Tiefpass,
	Spalttiefpass,
	Gaußtiefpass.

2

Geben Sie die äquivalente Bandbreite von  $H(f)$  an.

$\Delta f \ =\ $ $\ \rm kHz$

3

Berechnen Sie allgemein die Amplitude  $A_i$  in Abhängigkeit von  $x_i(t)$  und  $h(t)$. Welche der folgenden Punkte sind bei der Berechnung zu berücksichtigen?

	Beim Cosinussignal gilt  $A_i = y_i(t = 0)$.
	Es gilt  $y_i(t) = x_i(t) · h(t)$.
	Es gilt  $y_i(t) = x_i(t) ∗ h(t)$.

4

Welche der folgenden Ergebnisse treffen für  $A_0, A_2$  und  $A_4$  zu?   Es gilt weiterhin  $A_i = y_i(t = 0)$.

	$A_0 = 0$.
	$A_0 = 1 \hspace{0.05cm} \rm V $.
	$A_2 = 0$.
	$A_2 = 1 \hspace{0.05cm} \rm V $.
	$A_4 = 0$.
	$A_4 =1 \hspace{0.05cm} \rm V $.

5

Berechnen Sie die Amplituden  $A_1$  und  $A_3$  für ein  $1 \ \rm kHz$– bzw.  $3 \ \rm kHz$–Signal.
Interpretieren Sie die Ergebnisse anhand der Spektralfunktionen.

$A_1 \ = \ $ $\ \rm V$

$A_3 \ = \ $ $\ \rm V$

Musterlösung

Solution

(1)  Richtig ist der Lösungsvorschlag 2:   Es handelt sich um einen Spalttiefpass.

(2)  Die (äquivalente) Zeitdauer der Impulsantwort ist  $Δt = 0.5 \ \rm ms$.   Die äquivalente Bandbreite ist gleich dem Kehrwert:

$$Δf = 1/Δt \ \rm \underline{= \ 2 \ kHz}.$$

(3)  Richtig sind die Lösungsvorschläge 1 und 3:

• Da  $y_i(t)$  cosinusförmig ist, ist die Amplitude  $A_i = y_i(t = 0)$. Das Ausgangssignal wird hier über die Faltung berechnet:

$$A_i = y_i (t=0) = \int\limits_{ - \infty }^{ + \infty } {x_i ( \tau )} \cdot h ( {0 - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$

• Berücksichtigt man die Symmetrie und die zeitliche Begrenzung von  $h(t)$, so kommt man zum Ergebnis:

$$A_i = \frac{A_x}{\Delta t} \cdot \int\limits_{ - \Delta t /2 }^{ + \Delta t /2 } {\rm cos}(2\pi f_i \tau )\hspace{0.1cm}{\rm d}\tau.$$

(4)  Richtig sind die Lösungsvorschläge 2, 3 und 5:

• Beim Gleichsignal  $x_0(t) = A_x$  ist  $f_i = 0$  zu setzen und man erhält  $A_0 = A_x \ \rm \underline{ = \ 1 \hspace{0.05cm} V}$.
• Dagegen verschwindet bei den Cosinusfrequenzen  $f_2 = 2 \ \rm kHz$  und  $f_4 = 4 \ \rm kHz$  jeweils das Integral, da dann genau über eine bzw. zwei Periodendauern zu integrieren ist:   $A_2 \ \rm \underline{ = \hspace{0.05cm} 0}$  und  $A_4 \hspace{0.05cm} \rm \underline{ = \ 0}$.
• Im Frequenzbereich entsprechen die hier behandelten Fälle:

$$H(f=0) = 1, \hspace{0.3cm}H(f=\Delta f) = 0, \hspace{0.3cm}H(f=2\Delta f) = 0.$$

(5)  Das Ergebnis der Teilaufgabe  (3)  lautet unter Berücksichtigung der Symmetrie für  $f_i = f_1$:

$$A_1= \frac{2A_x}{\Delta t} \cdot \int\limits_{ 0 }^{ \Delta t /2 } {\rm cos}(2\pi f_1 \tau )\hspace{0.1cm}{\rm d}\tau = \frac{2A_x}{2\pi f_1 \cdot \Delta t} \cdot {\rm sin}(2\pi f_1 \frac{\Delta t}{2} )= A_x \cdot {\rm si}(\pi f_1 \Delta t ).$$

• Mit  $f_1 · Δt = 0.5$  lautet somit das Ergebnis:

$$A_1 = A_x \cdot {\rm si}(\frac{\pi}{2} ) = \frac{2A_x}{\pi} \hspace{0.15cm}\underline{= 0.637\,{\rm V}}.$$

• Entsprechend erhält man mit  $f_3 · Δt = 1.5$:

$$A_3 = A_x \cdot {\rm si}({3\pi}/{2} ) = -\frac{2A_x}{3\pi} = -{A_1}/{3}\hspace{0.15cm}\underline{= -0.212\,{\rm V}}.$$

• Genau zu den gleichen Ergebnissen – aber deutlich schneller – kommt man durch die Anwendung der Gleichung:

$$A_i = A_x · H(f = f_i).$$

• Bereits aus den Grafiken auf der Angabenseite erkennt man, dass das Integral über  $x_1(t)$  im markierten Bereich positiv und das Integral über  $x_3(t)$  negativ ist.
• Es ist allerdings anzumerken, dass man im Allgemeinen als Amplitude meist den Betrag bezeichnet (siehe Hinweis auf der Angabenseite).