Difference between revisions of "Aufgaben:Exercise 3.4: Characteristic Function"
From LNTwww
m (Text replacement - "[[Stochastische_Signaltheorie/" to "[[Theory_of_Stochastic_Signals/") |
|||
| Line 20: | Line 20: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[ | + | *Die Aufgabe gehört zum Kapitel [[Theory_of_Stochastic_Signals/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. |
| − | *Insbesondere wird auf die Seite [[ | + | *Insbesondere wird auf die Seite [[Theory_of_Stochastic_Signals/Erwartungswerte_und_Momente#Charakteristische_Funktion|Charakteristische Funktion]] Bezug genommen. |
*Die charakteristische Funktion einer zwischen $\pm a$ gleichverteilten Zufallsgröße $z$ lautet: | *Die charakteristische Funktion einer zwischen $\pm a$ gleichverteilten Zufallsgröße $z$ lautet: | ||
Revision as of 10:51, 9 July 2020
Gegeben seien hier die drei Zufallsgrößen $x$, $y$ und $z$ , meist durch ihre jeweiligen Wahrscheinlichkeitsdichtefunktionen:
- Über die Zufallsgröße $x$ ist nichts weiter bekannt: Diese kann sowohl eine diskrete als auch eine kontinuierliche Zufallsgröße sein und eine beliebige WDF $f_x(x)$ besitzen. Der Mittelwert ist allgemein gleich $m_x$.
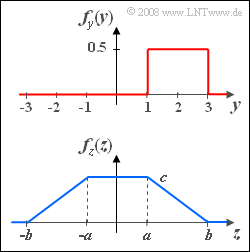
- Die kontinuierliche Zufallsgröße $y$ kann nur Werte im Bereich zwischen $1$ bis $3$ mit gleicher Wahrscheinlichkeit annehmen. Der Mittelwert ist $$m_y = 2.$$
- Die Zufallsgröße $z$ besitzt die folgende charakteristische Funktion:
- $$C_z ({\it \Omega} ) = {\mathop{\rm si}\nolimits}( {3{\it \Omega}} ) \cdot {\mathop{\rm si}\nolimits} ( {2{\it \Omega} } ).$$
- Daneben wird noch der qualitative Verlauf der WDF $f_z(z)$ entsprechend der blauen Skizze als bekannt vorausgesetzt. Zu bestimmen sind die WDF-Parameter $a$, $b$ und $c$ dieser WDF.
Hinweise:
- Die Aufgabe gehört zum Kapitel Erwartungswerte und Momente.
- Insbesondere wird auf die Seite Charakteristische Funktion Bezug genommen.
- Die charakteristische Funktion einer zwischen $\pm a$ gleichverteilten Zufallsgröße $z$ lautet:
- $$C_z ( {\it \Omega} ) = {\mathop{\rm si}\nolimits} ( {a {\it \Omega} } )\quad {\rm{mit}}\quad {\mathop{\rm si}\nolimits}( x ) = \sin ( x )/x.$$
Fragebogen
Musterlösung
(1) Richtig sind die Lösungsvorschläge 2, 3 und 4:
- $C_x ( {\it \Omega} )$ ist nicht die Fouriertransformierte zu $f_x(x)$, sondern die Fourierrücktransformierte:
- $$C_x( {\it \Omega } ) = \int_{ - \infty }^{ + \infty } {f_x }( x )\cdot {\rm{e}}^{\hspace{0.03cm}{\rm{j}}\hspace{0.03cm}{\it \Omega x}} \hspace{0.1cm}{\rm{d}}x .$$
- Auch bei dieser ist der Realteil stets gerade und der Imaginärteil ungerade. Für ${\it \Omega} = 0$ gilt:
- $$C_x( {\it \Omega} = 0 ) = \int_{ - \infty }^{ + \infty } {f_x }( x ) \hspace{0.1cm}{\rm{d}}x = 1.$$
- Die letzte Alternative trifft nicht immer zu: Eine zweipunktverteilte Zufallsgröße $x \in \{-1, +3\}$ mit den Wahrscheinlichkeiten $0.75$ und $0.25$ ist zwar mittelwertfrei $(m_x = 0)$, besitzt aber trotzdem eine komplexe charakteristische Funktion.
(2) Entsprechend der allgemeinen Definition gilt:
- $$C_y( {\it \Omega } ) = \int_{ - \infty }^{ + \infty } {f_y }( y )\cdot {\rm{e}}^{{\rm{j}}{\it \Omega y}} \hspace{0.1cm}{\rm{d}}y = 0.5\int_1^3 {{\rm{e}}^{{\rm{j}}\Omega y} \hspace{0.1cm}{\rm{d}}y.} $$
- Nach Lösen dieses Integrals ergibt sich:
- $$C_y ( {\it \Omega } ) = \frac{{{\rm{e}}^{{\rm{j}}3{\it \Omega } } - {\rm{e}}^{{\rm{j}}{\it \Omega } } }}{{2{\rm{j}}{\it \Omega } }} = \frac{{{\rm{e}}^{{\rm{j}}{\it \Omega } } - {\rm{e}}^{{\rm{ - j}}{\it \Omega }} }}{{2{\rm{j}}{\it \Omega } }} \cdot {\rm{e}}^{{\rm{j2}}{\it \Omega } } .$$
- Mit dem Satz von Euler kann hierfür auch geschrieben werden:
- $$C_y ( {\it \Omega } ) = \frac{{\sin ( {\it \Omega } )}}{{\it \Omega } } \cdot {\rm{e}}^{{\rm{j2}}{\it \Omega } } .$$
- Für ${\it \Omega} = \pi/2$ erhält man somit einen rein reellen Zahlenwert:
- $${\rm Re}[C_y ({\it \Omega} = {\rm{\pi }}/2 )] = \frac{{\sin( {{\rm{\pi }}/2})}}{{{\rm{\pi }}/2}} \cdot {\rm{e}}^{{\rm{j\pi }}} = - \frac{2}{{\rm{\pi }}} \hspace{0.15cm}\underline{\approx -0.637}, \hspace{0.5cm} {\rm Im}[C_y ({\it \Omega} = {\rm{\pi }}/2 )] \hspace{0.15cm}\underline{= 0} .$$
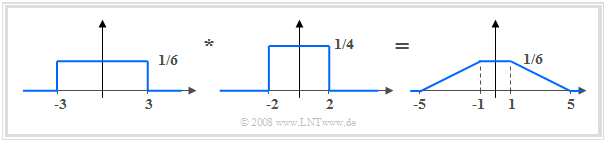
(3) Aus der angegebenen Korrespondenz kann abgelesen werden, dass ${\rm si}(3 {\it \Omega} )$ auf eine zwischen $\pm 3$ gleichverteilte Zufallsgröße zurückgeht und ${\rm si}(2 {\it \Omega} )$ die Transformierte einer Gleichverteilung zwischen $\pm 2$ angibt.
- In der charakteristischen Funktion sind diese beiden Anteile multiplikativ verknüpft. Damit ist die resultierende WDF $f_z(z)$ die Faltung dieser beiden Rechteckfunktionen:
- Die drei WDF-Parameter lauten somit:
- $$\hspace{0.15cm}\underline{a = 1},\quad \hspace{0.15cm}\underline{b = 5}, \quad c = 1/6 \hspace{0.15cm}\underline{= 0.167}.$$