Aufgaben:Exercise 5.2: Determination of the Frequency Response

• Return to book

Zur Bestimmung des Frequenzgangs  $H(f)$

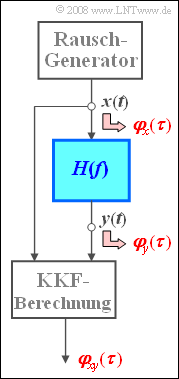
Wir betrachten die abgebildete Messanordnung zur Bestimmung des blau hervorgehobenen Frequenzgangs  $H(f)$.

• Das Eingangssignal  $x(t)$  ist weißes Gaußsches Rauschen mit der Rauschleistungsdichte  $N_0 = 10^{-10} \hspace{0.05cm} \rm W/Hz$.
• Somit gilt für die Autokorrelationsfunktion (AKF):

$$\varphi _x ( \tau ) = {N_0 }/{2} \cdot \delta ( \tau ).$$

• Die gemessene Kreuzkorrelationsfunktion (KKF) zwischen den Signalen  $x(t)$  und  $y(t)$  kann wie folgt angenähert werden
  $($nur gültig für positive Zeiten  $t)$:

$$\varphi _{xy} \left( \tau \right) = K \cdot {\rm{e}}^{ - \tau /T_0 },\hspace{0.5cm}\text{mit } \ K = 0.628 \cdot 10^{-12} \hspace{0.05cm} {\rm W}, \ T_0 = 1 \hspace{0.05cm} \rm ms.$$

• Gemessen wird außerdem die AKF  $\varphi_y(\tau)$  des Ausgangssignals  $y(t)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Stochastische Systemtheorie.
• Bezug genommen wird auch auf das Kapitel  Leistungsdichtespektrum.

• Beachten Sie bitte auch die folgende Fouriertransformation  $($in  $\omega)$:

$$H( \omega ) = \frac{1}{{1 + {\rm{j}}\cdot \omega /\omega _0 }}\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\,\hspace{0.15cm}h(t) = \omega _0 \cdot {\rm{e}}^{ - \omega _0 t} \hspace{0.3cm}(t \ge 0).$$

Für negative  $t$–Werte ist dagegen stets  $h(t) =0$.

Fragebogen

1

Welche der folgenden Aussagen treffen zu?  Man kann den Frequenzgang  $H(f)$  nach Betrag und Phase vollständig bestimmen, wenn

	die Funktionen  $\varphi_x(\tau)$  und  $\varphi_y(\tau)$  bekannt sind,
	die Funktionen  $\varphi_x(\tau)$  und  $\varphi_{xy}(\tau)$  bekannt sind,
	die Funktionen  $\varphi_{xy}(\tau)$  und  $\varphi_y(\tau)$  bekannt sind.

2

Berechnen Sie die Impulsantwort  $h(t)$.  Welcher Wert ergibt sich für  $t=T_0$?

$h(t = T_0) \ = \ $ $\ \cdot 10^{-3} \ \rm 1/s$

3

Wie lautet der Frequenzgang  $H(f)$?  Welcher Wert ergibt sich für $f= 0$?

$H(f = 0) \ = \ $

4

Berechnen Sie das Leistungsdichtespektrum des Ausgangssignals  $y(t)$.  Welcher Wert ergibt sich bei der Frequenz  $f = 1/(2\pi T_0)$?

${\it \Phi}_y(f = 1/(2\pi T_0)) \ = \ $ $\ \cdot 10^{-12}\ \rm W/Hz$

Musterlösung

Solution

(1)  Die Aussagen 2 und 3 sind zutreffend.

• Es gelten folgende Gleichungen:

$$\varphi _{xy} ( \tau ) = h( \tau ) * \varphi _x ( \tau )\quad \Rightarrow \quad H( f ) = \frac{{{\it \Phi} _{xy} ( f )}}{{{\it \Phi} _x ( f )}},$$

$$\varphi _y ( \tau) = \varphi _{xy} ( \tau) * h(- \tau)\quad \Rightarrow \quad H^{\star}( f ) = \frac{{{\it \Phi} _y ( f )}}{{{\it \Phi} _{xy} ( f )}}.$$

• Dagegen ist die erste Aussage falsch:   Bei der AKF-Berechnung gehen die Phasenbeziehungen verloren.
• Die zugehörigen Spektralfunktionen zu  $\varphi_x(\tau)$  und  $\varphi_x(\tau)$  – nämlich  ${\it \Phi}_x(f)$  und  ${\it \Phi}_y(f)$  – sind rein reell, so dass nur der Betrag  $|H(f)|$  angegeben werden kann.

(2)  Bei diracförmiger Eingangs-AKF  $\varphi_x(\tau)$  ist die Impulsantwort  $h(t)$  formgleich mit der KKF:

$$h(t) = \frac{{K \cdot {\rm{e}}^{ - t/T_0 } }}{N_0 /2} = 1.256 \cdot 10^{ - 2} \frac{1}{{\rm{s}}} \cdot {\rm{e}}^{ - t/T_0 } \hspace{0.3cm}\Rightarrow \hspace{0.3cm}h(t = T_0)\hspace{0.15cm}\underline{ = 4.62 \cdot 10^{-3}\ \rm 1/s}.$$

(3)  Die angegebene Fourierkorrespondenz lautet mit  $T_0 = 1/\omega_0$  und der Konstanten  $C= N_0/2 \cdot T_0/K$:

$$h(t) = \frac{C}{T_0 } \cdot {\rm{e}}^{ - t/T_0 }\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} H( \omega ) = \frac{C}{{1 + {\rm{j}}\omega T_0 }}.$$

• Die Konstante ergibt sich zu  $C = 0.08$.
• Mit  $H(f) = 2 \pi \cdot H(\omega)$  folgt daraus:

$$H(f) = \frac{0.5}{1 + {\rm{j2\pi }}fT_0 } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} H(f= 0) \hspace{0.15cm}\underline{=0.5}.$$

(4)  Für das Ausgangs-LDS gilt im Allgemeinen bzw. speziell hier:

$${\it \Phi}_y (f) = {\it \Phi} _x (f) \cdot \left| {H(f)} \right|^2 = \frac{N_0 }{2} \cdot \frac{0.5^2 }{{\left( {1 + {\rm{j2\pi }}fT_0 } \right)\left( {1 - {\rm{j2\pi }}fT_0 } \right)}} = {N_0 }/{8} \cdot \frac{1}{1 + \left( {{\rm{2\pi }}fT_0 } \right)^2 }.$$

• Bei der angegebenen Frequenz  $f = 1/(2\pi T_0)$  ist  ${\it \Phi}_y (f)$  gegenüber seinem Maximum bei  $f=0$  um die Hälfte abgefallen:

$${\it \Phi}_y (f = 1/(2 \pi T_0)) ={N_0 }/{16}\hspace{0.15cm} \underline{ = 6.25 \cdot 10^{ - 12} \;{\rm{W/Hz}}}.$$