Difference between revisions of "Applets:Das Gram-Schmidt-Verfahren"
| Line 146: | Line 146: | ||
Das Programm bietet insgesamt $4 \cdot 6 = 24$ Möglichkeiten zur Einstellung der jeweiligen Menge $\{s_i(t)\}$ möglicher Sendesignale. Diese $24$ Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt: | Das Programm bietet insgesamt $4 \cdot 6 = 24$ Möglichkeiten zur Einstellung der jeweiligen Menge $\{s_i(t)\}$ möglicher Sendesignale. Diese $24$ Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt: | ||
| − | '''(1)''' Rubrik <u>„Basisband”</u>: | + | '''(1)''' Rubrik <u>„Basisband”</u> ⇒ gültig für die Einstellungen $\rm (A)$ ... $\rm (F)$: |
| − | [[File: | + | [[File:Gram_1_neu_neu.png|right|frame|Signalform bei „Basisband”]] |
| − | * | + | *Jedes Mustersignal $s_i(t)$ besteht aus drei Rechteckfunktionen unterschiedlicher Höhen und jeweiliger Dauer $T$. |
| − | *Die einzelnen Rechteckhöhen sind Vielfache von $\pm 0.25$ und die gesamte Signaldauer | + | *Die einzelnen Rechteckhöhen sind Vielfache von $\pm 0.25$ und die gesamte Signaldauer ergibt $3T$. |
| − | *Solche Signale treten zum Beispiel bei der binären oder mehrstufigen [[Digitalsignalübertragung/Redundanzfreie_Codierung#Quatern.C3.A4rsignal_mit_rc_.3D_0_und_Tern.C3.A4rsignal_mit_rc_.E2.89.88_0|Basisbandübertragung]] auf. | + | *Mit dem seitlichen Slider kann man das Signal $s_i(t)$ um Vielfache von $\pm 0.25$ nach oben und unten verschieben. |
| − | + | *Solche Signale treten zum Beispiel bei der binären oder mehrstufigen [[Digitalsignalübertragung/Redundanzfreie_Codierung#Quatern.C3.A4rsignal_mit_rc_.3D_0_und_Tern.C3.A4rsignal_mit_rc_.E2.89.88_0|Basisbandübertragung]] auf. | |
| − | [[File: | + | *Im $\text{Beispiel 2}$ des angegebenen Links erkennt man die zum Beispiel grafischen Darstellungen |
| + | :* eines binären Signals $q(t)$, | ||
| + | :* eines ternären Signals $q(t)$, | ||
| + | :* eines quaternären Signals $q(t)$. | ||
| + | <br clear=all> | ||
| + | '''(1)''' Rubrik <u>„''M''–ASK / BPSK”</u> ⇒ gültig für die Einstellungen $\rm (G)$ ... $\rm (L)$: | ||
| + | [[File:Gram_2_neuneu.png|right|frame|Zum Gram-Schmidt-Verfahren|class=fit]] | ||
<br clear=all> | <br clear=all> | ||
==Versuchsdurchführung== | ==Versuchsdurchführung== | ||
Revision as of 16:05, 22 January 2020
Contents
Programmbeschreibung
Das Applet verdeutlicht die Augendiagramme für
- verschiedene Codierungen (binär–redundanzfrei, quaternär–redundanzfrei, pseudo–ternär: AMI und Duobinär) sowie
- verschiedene Empfangskonzepte (Matched–Filter–Empfänger, CRO–Nyquistsystem, gaußförmiges Empfangsfilter).
Das letzte Empfängerkonzept führt zu Impulsinterferenzen, das heißt: Benachbarte Symbole beeinträchtigen sich bei der Symbolentscheidung gegenseitig.
Solche Impulsinterferenzen und deren Einfluss auf die Fehlerwahrscheinlichkeit lassen sich durch das Augendiagramm sehr einfach erfassen und quantifizieren. Aber auch für die beiden anderen (impulsinterferenzfreien) Systeme lassen sich anhand der Grafiken wichtige Erkenntnisse gewinnen.
Ausgegeben wird zudem die ungünstigste („worst case”) Fehlerwahrscheinlichkeit $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$, die bei den binären Nyquistsystemen identisch mit der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$ ist und für die beiden anderen Systemvarianten eine geeignete obere Schranke darstellt: $p_{\rm U} \ge p_{\rm M}$.
In der $p_{\rm U}$–Gleichung bedeuten:
- ${\rm Q}(x)$ ist die Komplementäre Gaußsche Fehlerfunktion. Die normierte Augenöffnung kann Werte zwischen $0 \le ö_{\rm norm} \le 1$ annehmen.
- Der Maximalwert $(ö_{\rm norm} = 1)$ gilt für die binären Nyquistsysteme und $ö_{\rm norm}=0$ steht für ein „geschlossenes Auge”.
- Der normierte Detektionsrauscheffektivwert $\sigma_{\rm norm}$ hängt vom einstellbaren Parameter $10 \cdot \lg \ E_{\rm B}/N_0$ ab, aber auch von der Codierung und vom Empfängerkonzept.
Theoretischer Hintergrund
Signaldarstellung mit orthonormalen Basisfunktionen
Wir gehen von einer Menge $\{s_i(t)\}$ möglicher Sendesignale aus, die den möglichen Nachrichten $m_i$ eineindeutig zugeordnet sind. Mit $i = 1$, ... , $M$ gelte:
- $$m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: \hspace{0.3cm} m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.$$
Für das Folgende setzen wir weiter voraus, dass die $M$ Signale $s_i(t)$ energiebegrenzt sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind.
$\text{Satz:}$ Eine jede Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale lässt sich in $N \le M$ orthonormale Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ entwickeln. Es gilt:
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$
Jeweils zwei Basisfunktionen $\varphi_j(t)$ und $\varphi_k(t)$ müssen orthonormal zueinander sein, das heißt, dass gelten muss $(\delta_{jk}$ nennt man das Kronecker–Symbol$)$:
- $$<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.1cm}j = k \\ {\rm falls}\hspace{0.1cm} j \ne k \\ \end{array} \hspace{0.05cm}.$$
Der Parameter $N$ gibt dabei an, wieviele Basisfunktionen $\varphi_j(t)$ benötigt werden, um die $M$ möglichen Sendesignale darzustellen. Mit anderen Worten: $N$ ist die Dimension des Vektorraums, der von den $M$ Signalen aufgespannt wird. Dabei gilt:
- Ist $N = M$, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien $E_i = <\hspace{-0.1cm}s_i(t), \hspace{0.05cm}s_i(t) \hspace{-0.1cm}>$ können durchaus ungleich Eins sein.
- Der Fall $N < M$ ergibt sich, wenn mindestens ein Signal $s_i(t)$ als Linearkombination von Basisfunktionen $\varphi_j(t)$ dargestellt werden kann, die sich aus anderen Signalen $s_j(t) \ne s_i(t)$ ergeben haben.
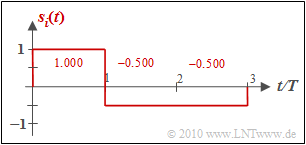
$\text{Beispiel 1:}$ Wir betrachten $M = 3$ energiebegrenzte Signale gemäß der Grafik.
Man erkennt sofort:
- Die Signale $s_1(t)$ und $s_2(t)$ sind zueinander orthogonal.
- Die Energien sind $E_1 = A^2 \cdot T = E$ und $E_2 = (A/2)^2 \cdot T = E/4$.
- Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sind jeweils formgleich mit $s_1(t)$ bzw. $s_2(t)$.
- Beide Signale besitzen jeweils die Energie „Eins”:
- $$\varphi_1(t)=\frac{s_1(t)}{\sqrt{E_1} } = \frac{s_1(t)}{\sqrt{A^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_1(t)}{A}$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},$$
- $$\varphi_2(t) =\frac{s_2(t)}{\sqrt{E_2} } = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = {\sqrt{E} }/{2}\hspace{0.05cm}.$$
- Das Signal $s_3(t)$ kann durch die vorher bestimmten Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ ausgedrückt werden:
- $$s_3(t) =s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},$$
- $$\hspace{0.5cm}\Rightarrow \hspace{0.1cm} s_{31} = {A}/{2} \cdot \sqrt {T}= {\sqrt{E} }/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.$$
Trotz $M=3$ gilt also im vorliegenen Fall nur $N=2$.
Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ als Achsen dargestellt, wobei $E = A^2 \cdot T$ gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist.
Die vektoriellen Repräsentanten der Signale $s_1(t)$, $s_2(t)$ und $s_3(t)$ in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen:
- $$\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.5cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.5cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.$$
Das Verfahren nach Gram-Schmidt
Im letzten $\text{Beispiel}$ war die Bestimmung der beiden orthonormalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sehr einfach, da diese formgleich mit $s_1(t)$ bzw. $s_2(t)$ waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_N(t)$ für beliebig vorgebbare Signale $s_1(t)$, ... , $s_M(t)$, und zwar wie folgt:
- Die erste Basisfunktion $\varphi_1(t)$ ist stets formgleich mit $s_1(t)$. Es gilt:
- $$\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 \hspace{0.05cm}.$$
$\text{Hinweise zur Nomenklatur:}$
(1) Ausgehend von zwei reellen und energiebegrenzten Zeitfunktionen $x(t)$ und $y(t)$ erhält man für das innere Produkt allgemein:
- $$<\hspace{-0.1cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.1cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t \hspace{0.05cm}.$$
(2) Daraus ergibt sich die Euklidische Norm der Zeitfunktion $s_1(t)$:
- $$\vert \vert s_1(t) \vert \vert = \sqrt{<\hspace{-0.1cm}s_1(t), \hspace{0.15cm}s_1(t) \hspace{-0.1cm}>} $$
Es wird nun angenommen, dass aus den Signalen $s_1(t)$, ... , $s_{k-1}(t)$ bereits die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ berechnet wurden $(n \le k)$.
- Dann berechnen wir mittels der nächsten Funktion $s_k(t)$ die Hilfsfunktion
- $$\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm}, n-1\hspace{0.05cm}.$$
- Hat diese Hilfsfunktion die Norm $||\theta_k(t)|| = 0$, so liefert $s_k(t)$ keine neue Basisfunktion. Vielmehr lässt sich dann $s_k(t)$ durch die $n-1$ bereits vorher gefundenen Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ ausdrücken:
- $$s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.$$
- Eine neue Basisfunktion (nämlich die $n$–te) ergibt sich nur für den Fall $||\theta_k(t)|| \ne 0$:
- $$\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.$$
Diese Prozedur wird solange fortgesetzt, bis alle $M$ Signale berücksichtigt wurden.
- Danach hat man alle $N \le M$ orthonormalen Basisfunktionen $\varphi_j(t)$ gefunden.
- Der Sonderfall $N = M$ ergibt sich nur dann, wenn alle $M$ Signale linear voneinander unabhängig sind.
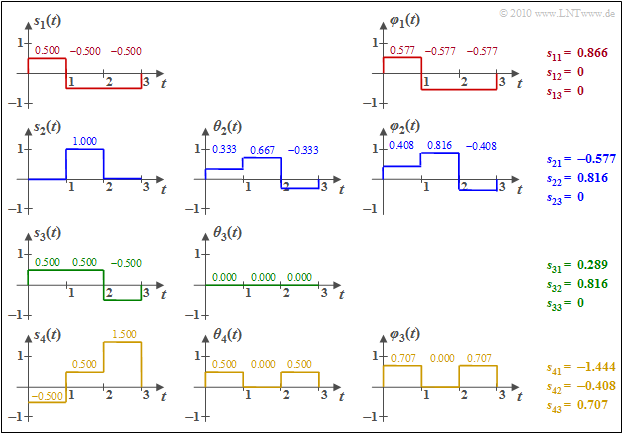
$\text{Beispiel 2:}$ Wir betrachten die $M = 4$ energiebegrenzten Signale $s_1(t)$, ... , $s_4(t)$ entsprechend der Grafik. Zur Vereinfachung der Berechnungen sind hier sowohl die Amplituden als auch die Zeit normiert.
Man erkennt aus diesen Skizzen:
- Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$. Wegen $E_1 = \vert \vert s_1(t) \vert \vert ^2 = 3 \cdot 0.5^2 = 0.75$ ergibt sich $s_{11} = \vert \vert s_1(t) \vert \vert = 0.866$. $\varphi_1(t)$ selbst besitzt abschnittsweise die Werte $\pm 0.5/0.866 = \pm0.577$.
- Zur Berechnung der Hilfsfunktion $\theta_2(t)$ berechnen wir
- $$s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577$$
- $$ \Rightarrow \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, \hspace{0.15cm} 0.667, \hspace{0.15cm} -0.333) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\vert \vert \theta_2(t) \vert \vert^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667$$
- $$ \Rightarrow \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.3cm} \varphi_2(t) = \theta_2(t)/s_{22} = (0.408, \hspace{0.15cm} 0.816, \hspace{0.15cm} -0.408)\hspace{0.05cm}. $$
- Die inneren Produkte zwischen $s_1(t)$ mit $\varphi_1(t)$ bzw. $\varphi_2(t)$ liefern folgende Ergebnisse:
- $$s_{31} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289$$
- $$s_{32} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816$$
- $$\Rightarrow \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.$$
Das bedeutet: Die grüne Funktion $s_3(t)$ liefert keine neue Basisfunktion $\varphi_3(t)$, im Gegensatz zur Funktion $s_4(t)$. Die numerischen Ergebnisse hierfür können der Grafik entnommen werden.
Die verschiedenen Rubriken bei der Auswahl der Programmparameter
Das Programm bietet insgesamt $4 \cdot 6 = 24$ Möglichkeiten zur Einstellung der jeweiligen Menge $\{s_i(t)\}$ möglicher Sendesignale. Diese $24$ Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt:
(1) Rubrik „Basisband” ⇒ gültig für die Einstellungen $\rm (A)$ ... $\rm (F)$:
- Jedes Mustersignal $s_i(t)$ besteht aus drei Rechteckfunktionen unterschiedlicher Höhen und jeweiliger Dauer $T$.
- Die einzelnen Rechteckhöhen sind Vielfache von $\pm 0.25$ und die gesamte Signaldauer ergibt $3T$.
- Mit dem seitlichen Slider kann man das Signal $s_i(t)$ um Vielfache von $\pm 0.25$ nach oben und unten verschieben.
- Solche Signale treten zum Beispiel bei der binären oder mehrstufigen Basisbandübertragung auf.
- Im $\text{Beispiel 2}$ des angegebenen Links erkennt man die zum Beispiel grafischen Darstellungen
- eines binären Signals $q(t)$,
- eines ternären Signals $q(t)$,
- eines quaternären Signals $q(t)$.
(1) Rubrik „M–ASK / BPSK” ⇒ gültig für die Einstellungen $\rm (G)$ ... $\rm (L)$:
Versuchsdurchführung
Noch anpassen
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
Bis hierher
(1) Es gilt die Einstellung $\rm A$. Interpretieren Sie die ausgegebenen Grafiken. Wählen Sie hierfür „Einzelschritt”.
- Einstellung $\rm A$ beschreibt das $\text{Beispiel 2}$ im Theorieteil. Die Basisfunktion $\varphi_1(t)$ ist identisch mit dem Signal $s_1(t)$, aber mit Signalenergie $E=1$.
- Es gibt hier nur $N=3$ Basisfunktionen, da die Hilfsfunktion $\theta_3(t)$ identisch Null ist.
- Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ können im 3D–Vektorraum abgelesen werden; Beispiel: $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
(2) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm B$. Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”.
- Auch hier gibt es $N=3$ Basisfunktionen. Bei Änderung auf $s_4 = (-1, \hspace{0.15cm} -1, \hspace{0.25cm} 0)$ nur mehr $N=2$.
(3) Bei der Einstellung $\rm C$ ist die Reihenfolge der Signale gegenüber $\rm B$ vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?
- Auch hier gibt es $N=3$ Basisfunktionen, aber nun andere: Nämlich $\varphi_1(t) = s_1(t)$, $\varphi_2(t) = s_2(t)$, $\varphi_3(t) = s_3(t)$.
(4) Die $M=4$ Signale der Einstellung $\rm D$ lassen sich durch nur $N=2$ Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.
- Carolin bitte lösen. Ich bin zu blöd. $s_3$ als Linearkombination von $s_1$ und $s_2$ schreiben. Ebenso $s_4$.
(5) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm E$ im Vergleich zur Einstellung $\rm D$.
- Bei der Einstellung $\rm E$ ist die Reihenfolge der Signale gegenüber der Einstellung $\rm D$ vertauscht. Ähnlich wie zwischen $\rm B$ und $\rm C$.
- Auch diese $M=4$ Signale lassen sich somit durch nur $N=2$ Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe (4).
(6) Ab hier dann neu machen.
- Für $T_{\rm E}/T < 1$ gilt weiterhin $ö_{\rm norm}= 1$. Aber $\sigma_{\rm norm}$ wird größer, zum Beispiel $\sigma_{\rm norm} = 0.316$ für $T_{\rm E}/T =0.5$ ⇒ das Filter ist zu breitbandig!
- Für $T_{\rm E}/T > 1$ ergibt sich im Vergleich zu (5) ein kleineres $\sigma_{\rm norm}$. Aber Das Auge ist nicht mehr geöffnet. $T_{\rm E}/T =1.25$: $ö_{\rm norm}= g_0 - 2 \cdot g_1 = 0.6$.
(7) Wählen Sie nun die Einstellungen $M=2 \text{, CRO–Nyquist, }r_f = 0.2$ sowie „Auge – Gesamt”. Interpretieren Sie das Augendiagramm, auch für andere $r_f$–Werte.
- Im Gegensatz zu (6) ist hier der Grundimpuls für $|t|>T$ nicht Null, aber $g_d(t)$ hat äquidistane Nulldurchgänge: $g_0 = 1, \ g_1 = g_2 = 0$ ⇒ Nyquistsystem.
- Alle $32$ Augenlinien gehen bei $t=0$ durch nur zwei Punkte. Die vertikale Augenöffnung ist für alle $r_f$ maximal ⇒ $ö_{\rm norm}= 1$.
- Dagegen nimmt die horizontale Augenöffnung mit $r_f$ zu und ist $r_f = 1$ maximal gleich $T$ ⇒ Phasenjitter hat in diesem Fall nur geringen Einfluss.
(8) Gleiche Einstellung wie in (7). Variieren Sie nun $r_f$ im Hinblick auf minimale Fehlerwahrscheinlichkeit. Interpretieren Sie die Ergebnisse.
- $ö_{\rm norm}= 1$ gilt stets. Dagegen zeigt $\sigma_{\rm norm}$ eine leichte Abhängigkeit von $r_f$. DasMinimum $\sigma_{\rm norm}=0.236$ ergibt sich für $r_f = 0.9$ ⇒ $p_{\rm U} \approx 1.1 \cdot 10^{-5}.$
- Gegenüber dem bestmöglichen Fall gemäß (7) „Matched–Filter–Empfänger” ist $p_{\rm U}$ dreimal so groß, obwohl $\sigma_{\rm norm}$ nur um ca. $5\%$ größer ist.
- Der größere $\sigma_{\rm norm}$–Wert geht auf die Überhöhung des Rausch–LDS zurück, um den Abfall durch den Sender–Frequenzgang $H_{\rm S}(f)$ auszugleichen.
(9) Wählen Sie die Einstellungen $M=4 \text{, nach Spalt–TP, }T_{\rm E}/T = 1$, $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ und $12 \ {\rm dB}$. Interpretieren Sie die Ergebnisse.
- Es gibt nun drei Augenöffnungen. Gegenüber (5) ist also $ö_{\rm norm}$ um den Faktor $3$ kleiner, $\sigma_{\rm norm}$ dagegen nur um etwa den Faktor $\sqrt{5/9)} \approx 0.75$.
- Für $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ ergibt sich nun die Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2.27\%$ und für $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$ nur mehr $0.59\%$.
(10) Für die restlichen Aufgaben gelte stets $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Betrachten Sie das Augendiagramm für $M=4 \text{, CRO–Nyquist, }r_f = 0.5$.
- In $d_{\rm S}(t)$ müssen alle „Fünf–Symbol–Kombinationen” enthalten sein ⇒ mindestens $4^5 = 1024$ Teilstücke ⇒ maximal $1024$ unterscheidbare Linien.
- Alle $1024$ Augenlinien gehen bei $t=0$ durch nur vier Punkte: $ö_{\rm norm}= 0.333$. $\sigma_{\rm norm} = 0.143$ ist etwas größer als in (9) ⇒ ebenso $p_{\rm U} \approx 1\%$.
(11) Wählen Sie die Einstellungen $M=4 \text{, nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ und variieren Sie $f_{\rm G}/R_{\rm B}$. Interpretieren Sie die Ergebnisse.
- $f_{\rm G}/R_{\rm B}=0.48$ führt zur minimalen Fehlerwahrscheinlichkeit $p_{\rm U} \approx 0.21\%$. Kompromiss zwischen $ö_{\rm norm}= 0.312$ und $\sigma_{\rm norm}= 0.109$.
- Bei zu kleiner Grenzfrequenz dominieren die Impulsinterferenzen. Beispiel: $f_{\rm G}/R_{\rm B}= 0.3$: $ö_{\rm norm}= 0.157; $ $\sigma_{\rm norm}= 0.086$ ⇒ $p_{\rm U} \approx 3.5\%$.
- Bei zu großer Grenzfrequenz dominiert das Rauschen. Beispiel: $f_{\rm G}/R_{\rm B}= 1.0$: $ö_{\rm norm}= 0.333; $ $\sigma_{\rm norm}= 0.157$ ⇒ $p_{\rm U} \approx 1.7\%$.
- Aus dem Vergleich mit (9) erkennt man: Bei Quaternärcodierung ist es günstiger, Impulsinterferenzen zuzulassen.
(12) Welche Unterschiede zeigt das Auge für $M=3 \text{ (AMI-Code), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ gegenüber dem vergleichbaren Binärsystem? Interpretation.
- Der Detektionsgrundimpuls $g_d(t)$ ist in beiden Fällen gleich. Die Abtastwerte sind jeweils $g_0 = 0.771, \ g_1 = 0.114$.
- Beim AMI–Code gibt es zwei Augenöffnungen mit je $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1) = 0.214$. Beim Binärcode: $ö_{\rm norm}= g_0 -2 \cdot g_1 = 0.543$.
- Die AMI–Folge besteht zu 50% aus Nullen. Die Symbole $+1$ und $-1$ wechseln sich ab ⇒ es gibt keine lange $+1$–Folge und keine lange $-1$–Folge.
- Darin liegt der einzige Vorteil des AMI–Codes: Dieser kann auch bei einem gleichsignalfreien Kanal ⇒ $H_{\rm K}(f= 0)=0$ angewendet werden.
(13) Gleiche Einstellung wie in (12), zudem $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Analysieren Sie die Fehlerwahrscheinlichkeit des AMI–Codes.
- Trotz kleinerem $\sigma_{\rm norm} = 0.103$ hat der AMI–Code eine höhere Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2\%$ als der Binärcode: $\sigma_{\rm norm} = 0.146, \ p_{\rm U} \approx \cdot 10^{-4}.$
- Für $f_{\rm G}/R_{\rm B}<0.34$ ergibt sich ein geschlossenes Auge $(ö_{\rm norm}= 0)$ ⇒ $p_{\rm U} =50\%$. Beim Binärcode: Für $f_{\rm G}/R_{\rm B}>0.34$ ist das Auge geöffnet.
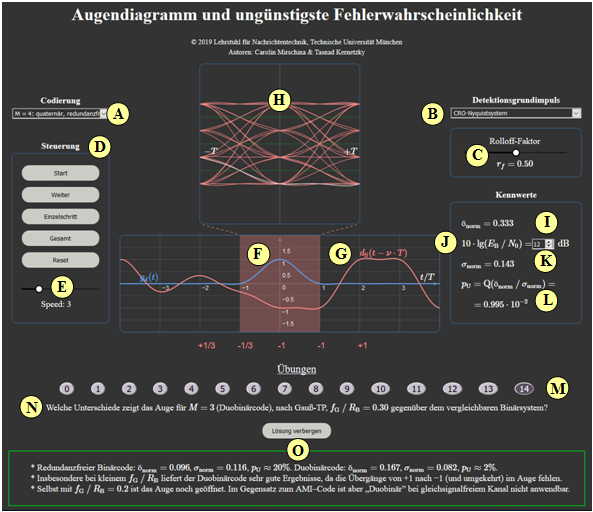
(14) Welche Unterschiede zeigt das Auge für $M=3 \text{ (Duobinärcode), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.30$ gegenüber dem vergleichbaren Binärsystem?
- Redundanzfreier Binärcode: $ö_{\rm norm}= 0.096, \ \sigma_{\rm norm} = 0.116 \ p_{\rm U} \approx 20\% $ Duobinärcode: $ö_{\rm norm}= 0.167, \ \sigma_{\rm norm} = 0.082 \ p_{\rm U} \approx 2\% $.
- Insbesondere bei kleinem $f_{\rm G}/R_{\rm B}$ liefert der Duobinärcode gute Ergebnisse, da die Übergänge von $+1$ nach $-1$ (und umgekehrt) im Auge fehlen.
- Selbst mit $f_{\rm G}/R_{\rm B}=0.2$ ist das Auge noch geöffnet. Im Gegensatz zum AMI–Code ist aber „Duobinär” bei gleichsignalfreiem Kanal nicht anwendbar.
Zur Handhabung des Applets
(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)
(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}
(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)
(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)
(E) Geschwindigkeit der Augendiagrammdarstellung
(F) Darstellung: Detektionsgrundimpuls $g_d(t)$
(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$
(H) Darstellung: Augendiagramm im Bereich $\pm T$
( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)
(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)
(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)
(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)
(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(N) Bereich für die Versuchsdurchführung: Aufgabenstellung
(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2008 von Thomas Großer im Rahmen einer Werkstudententätigkeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.