Aufgaben:Exercise 1.1Z: Simple Path Loss Model

• Return to book

Bandbreitenorganisation bei DSL

Funkübertragung bei Sichtverbindung lässt sich durch das so genannte Pfadverlustmodell beschreiben, das durch folgende Gleichungen gegeben ist:

$$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$

$$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$

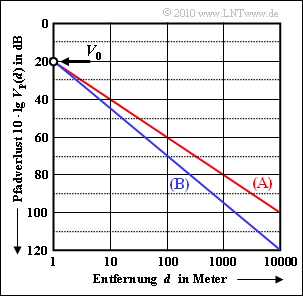
Die Grafik zeigt den Pfadverlust  $V_{\rm P}(d)$  in  $\rm dB$. Auch die Abszisse  $d$  ist logarithmisch dargestellt.

In obiger Gleichung sind verwendet:

• die Distanz  $d$  von Sender und Empfänger,
• die Bezugsentfernung  $d_0 = 1 \ \rm m$,
• der Pfadverlustexponent  $\gamma$,
• die Wellenlänge  $\lambda$  der elektromagnetischen Welle.

Gezeigt sind zwei Szenarien  $\rm (A)$  und  $\rm (B)$  mit gleichem Pfadverlust bei der Distanz  $d_0 = 1 \ \rm m$:

$$V_{\rm 0} = V_{\rm P}(d = d_0) = 20\,{\rm dB} \hspace{0.05cm}.$$

Eines dieser beiden Szenarien beschreibt die so genannte Freiraumdämpfung, charakterisiert durch den Pfadverlustexponenten  $\gamma = 2$. Die Gleichung für die Freiraumdämpfung gilt allerdings nur im Fernfeld, also wenn der Abstand  $d$  zwischen Sender und Empfänger größer ist als die „Fraunhofer–Distanz”

$$d_{\rm F} = {2 D^2}/{\lambda} \hspace{0.05cm}.$$

Hierbei ist  $D$  die größte physikalische Abmessung der Sendeantenne. Bei einer  $\lambda/2$–Antenne erhält man hierfür das einfache Ergebnis:

$$d_{\rm F} = \frac{2 \cdot (\lambda/2)^2}{\lambda} = {\lambda}/{2}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Distanzabhängige Dämpfung und Abschattung.
• Die Lichtgeschwindigkeit beträgt  $c = 3 \cdot 10^8 \ {\rm m/s}$.

Fragebogen

1

Welche Pfadverlustexponenten gelten für die Szenarien  $\rm (A)$  und  $\rm (B)$?

$\gamma_{\rm A}\ = \ $

$\gamma_{\rm B} \ = \ $

2

Welches Szenario beschreibt die Freiraumdämpfung?

	Szenario  $\rm (A)$,
	Szenario  $\rm (B)$.

3

Welche Signalfrequenzen liegen den Szenarien  $\rm (A)$  und  $\rm (B)$  zugrunde?

$f_{\rm A} \ = \ $ $\ \rm MHz$

$f_{\rm B} \ = \ $ $\ \rm MHz$

4

Gilt das Freiraum–Szenario für alle Distanzen zwischen  $1 \ \rm m$  und  $10 \ \rm km$?

	Ja,
	Nein.

Musterlösung

Solution

(1)  Die (einfachste) Pfadverlustgleichung lautet:

$$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm}.$$

• Beim Szenario (A) beträgt der Abfall pro Dekade (zum Beispiel zwischen $d_0 = 1 \ \rm m$ und $d = 10 \ \rm m$) genau $20 \ \rm dB$ und beim Szenario (B) $25 \ \rm dB$.
• Daraus folgt:

$$\gamma_{\rm A} \hspace{0.15cm} \underline{= 2}\hspace{0.05cm},\hspace{0.2cm}\gamma_{\rm B} \hspace{0.15cm} \underline{= 2.5}\hspace{0.05cm}.$$

(2)  Richtig ist Lösungsvorschlag 1, da die Freiraumdämpfung durch den Pfadverlustexponenten $\gamma = 2$ gekennzeichnet ist.

(3)  Der Pfadverlust bei $d_0 = 1 \ \rm m$ ist in beiden Fällen $V_0 = 20 \ \rm dB$. Beim Szenario (A) gilt weiter:

$$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}}\right ]^2 = 20\,{\rm dB} \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}} = 10 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \lambda_{\rm A} = 4 \pi \cdot 0.1\,{\rm m} = 1.257\,{\rm m} \hspace{0.05cm}.$$

• Die Frequenz $f_{\rm A}$ hängt mit der Wellenlänge $\lambda_{\rm A}$ über die Lichtgeschwindigkeit $c$ zusammen:

$$f_{\rm A} = \frac{c}{\lambda_{\rm A}} = \frac{3 \cdot 10^8\,{\rm m/s}}{1.257\,{\rm m}} = 2.39 \cdot 10^8\,{\rm Hz} \hspace{0.15cm} \underline{\approx 240 \,\,{\rm MHz}} \hspace{0.05cm}.$$

• Dagegen gilt für das Szenario (B):

$$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ]^{2.5} = 20\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 25 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ] = 20\,{\rm dB}$$

$$\Rightarrow \hspace{0.3cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}} = 10^{0.8} \approx 6.31 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\lambda_{\rm B}} = \frac{10}{6.31} \cdot {\lambda_{\rm A}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {f_{\rm B}} = \frac{6.31}{10} \cdot {f_{\rm A}} = 0.631 \cdot 240 \,{\rm MHz}\hspace{0.15cm} \underline{\approx 151.4 \,\,{\rm MHz}} \hspace{0.05cm}.$$

(4)  Richtig ist der erste Lösungsvorschlag:

• Beim Freiraum–Szenario (A) beträgt die Fraunhofer–Distanz  $d_{\rm F} = \lambda_{\rm A}/2 \approx 63 \ \rm cm$. Es gilt also stets  $d > d_{\rm F}$.
• Auch beim Szenario (B) ist wegen  $\lambda_{\rm B} \approx 2 \ \rm m$  bzw.  $d_{\rm F} \approx 1 \ \rm m$  der gesamte dargestellte Verlauf richtig.