Difference between revisions of "Aufgaben:Exercise 1.7: PDF of Rice Fading"
m (Javier verschob die Seite Exercises:Exercise 1.7: PDF of Rice Fading nach Exercise 1.7: PDF of Rice Fading) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID2133__Mob_A_1_7.png|right|frame| Rice-Fading für verschiedene Werte von $|z_0|^2$]] | [[File:P_ID2133__Mob_A_1_7.png|right|frame| Rice-Fading für verschiedene Werte von $|z_0|^2$]] | ||
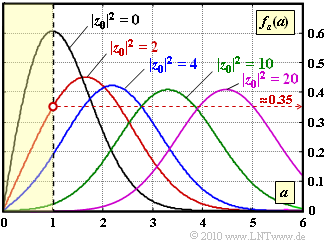
| − | + | As you can see in the diagram, we consider the same scenario as in [[Aufgaben:Exercise_1.6:_ACF_and_PSD_of_Rice_Fading| Exercise 1.6]]: | |
| − | * <i>Rice | + | * <i>Rice fading</i> with variance $\sigma^2 = 1$ the Gaussian processes and the parameter $|z_0|$ for the direct path. |
| − | * | + | * Regarding direct path, we are interested in the parameter values $|z_0|^2 = 0, \ 2, \ 4, \ 10, \ 20$ (see graphic). |
| − | * | + | * The WDF of the amount $a(t) = |z(t)|$ is |
| − | :$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}. | + | :$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}.$ |
| − | * | + | * For example, the modified zero-order Bessel function returns the following values: |
| − | + | $${\rm I }_0 (2) = 2.28\hspace{0.05cm},\hspace{0.2cm}{\rm I }_0 (4) = 11.30\hspace{0.05cm},\hspace{0.2cm}{\rm I }_0 (3) = 67.23 | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The quadratic expectation value ⇒ power of the multiplicative factor $|z(t)|$, is equal |
| − | + | $${\rm E}\left [ a^2 \right ] = {\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * With $z_0 = 0$ the <i>Rice fading</i> becomes the more critical <i>Rayleigh fading</i>. In this case, the probability that $a$ lies in the yellow-shaded area between $0$ and $1$ applies: |
| − | + | $$$ {\rm Pr}(a \le 1) = 1 - {\rm e}^{-0.5/\sigma^2} \approx 0.4 | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In | + | In this task the probability ${\rm Pr}(a ≤ 1)$ for $|z_0| ≠ 0$ is to be approximated. There are two ways to do this, namely: |
| − | * | + | * the <i>triangular approximation</i>: |
| − | + | $${\rm Pr}(a \le 1) = {1}/{2} \cdot f_a(a=1) | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * the <i> Gaussian approximation</i>: Actual $|z_0| \gg \sigma$, then the Rice distribution can be approximated by a Gaussian distribution with mean $|z_0|$ and scatter $\sigma$ . |
| Line 29: | Line 29: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * The task belongs to chapter [[Mobile_Communication/Non-Frequency Selective_Fading_with_Direct Component|Non-Frequency Selective Fading with Direct Component]]. |
| − | * | + | * For the numerical solutions to the last subtasks, we recommend the interaction moduleApplets [[Applets:Complementary_Gaussian_Error Functions_(new_Applet)|Complementary Gaussian Error Functions]]. |
| − | === | + | ===Questionnaire== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate some WDF–values for $|z_0| = 0$ and $\sigma = 2$: |
|type="{}"} | |type="{}"} | ||
$f_a(a = 1) \ = \ ${ 0.187 3% } | $f_a(a = 1) \ = \ ${ 0.187 3% } | ||
| Line 44: | Line 44: | ||
$f_a(a = 3) \ = \ ${ 0.303 3% } | $f_a(a = 3) \ = \ ${ 0.303 3% } | ||
| − | { | + | {It be $|z_0| = 2$ ⇒ $|z_0|^2 = 4$ ('''blue curve''). How big is ${\rm Pr}(a ≤ 1)$? Use the '''triangular approximation''. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(a ≤ 1)\ = \ ${ 9.4 3% } $\ \%$ | + | ${\rm Pr}(a ≤ 1)\ = \ ${ 9.4 3% } $\ \ \%$ |
| − | { | + | {It be $|z_0|^2 = 2$ (''red curve''). How big is ${\rm Pr}(a ≤ 1)$? Use the '''triangular approximation''. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(a ≤ 1) \ = \ ${ 17.5 3% } $\ \ | + | ${\rm Pr}(a ≤ 1) \ = \ ${ 17.5 3% } $\ \ \ |
| − | { | + | {It be $|z_0|^2 = 10$ (''green curve''). How big is ${\rm Pr}(a ≤ 1)$? Use the '''Gauss approximation''. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(a ≤ 1) \ = \ ${ 1.5 3% } $\ \ | + | ${\rm Pr}(a ≤ 1) \ = \ ${ 1.5 3% } $\ \ \ |
| − | { | + | {It be $|z_0|^2 = 20$ (''purple curve''). How big is ${\rm Pr}(a ≤ 1)$? Use the '''Gaussian approximation''. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(a ≤ 1) \ = \ ${ 0.02 3% } $\ \ | + | ${\rm Pr}(a ≤ 1) \ = \ ${ 0.02 3% } $\ \ $ |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
| − | {{ML-Kopf}} | + | {{{ML-Kopf}} |
| − | '''(1)''' | + | '''(1)''' With $|z_0| = 2$ and $\sigma = 2$ the Rice–WDF can be represented as follows |
| − | + | $$f_a(a) = a \cdot {\rm exp} [ -\frac{a^2 + 4}{2}] \cdot {\rm I}_0 (2a)\hspace{0.05cm}.$ | |
| − | * | + | *This gives the values searched for: |
:$$f_a(a = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \cdot {\rm e}^{-2.5} \cdot {\rm I}_0 (2) = 0.082 \cdot 2.28 \hspace{0.15cm} \underline{ = 0.187}\hspace{0.05cm},$$ | :$$f_a(a = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \cdot {\rm e}^{-2.5} \cdot {\rm I}_0 (2) = 0.082 \cdot 2.28 \hspace{0.15cm} \underline{ = 0.187}\hspace{0.05cm},$$ | ||
:$$f_a(a = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm e}^{-4} \cdot {\rm I}_0 (4) = 2 \cdot 0.0183 \cdot 11.3 \hspace{0.15cm} \underline{ = 0.414}\hspace{0.05cm},$$ | :$$f_a(a = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm e}^{-4} \cdot {\rm I}_0 (4) = 2 \cdot 0.0183 \cdot 11.3 \hspace{0.15cm} \underline{ = 0.414}\hspace{0.05cm},$$ | ||
:$$f_a(a = 3) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \cdot {\rm e}^{-6.5} \cdot {\rm I}_0 (6) = 3 \cdot 0.0015 \cdot 67.23 \hspace{0.15cm} \underline{ = 0.303}\hspace{0.05cm}.$$ | :$$f_a(a = 3) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \cdot {\rm e}^{-6.5} \cdot {\rm I}_0 (6) = 3 \cdot 0.0015 \cdot 67.23 \hspace{0.15cm} \underline{ = 0.303}\hspace{0.05cm}.$$ | ||
| − | * | + | *The results fit well with the blue curve on the specifications page. |
| − | '''(2)''' | + | '''(2)''' With the result of the subtask '''(1)''' ⇒ $f_a(a = 1) = 0.187$ is obtained with the triangle approximation: |
| − | + | $${\rm Pr}(a \le 1) = {1}/{2} \cdot 0.187 \cdot 1\hspace{0.15cm} \underline{ \approx 9.4\,\%} \hspace{0.05cm}.$$ | |
| − | * | + | *This result will be a bit too large, because the blue curve is below the connecting line from $(0, 0)$ to $(1, 0.187)$ ⇒ convex curve. |
| + | '''(3)''' For the red curve the WDF–value $f_a(a = 1) \approx 0.35$ can be read from the [[Tasks:1.7_WDF_des_Rice%E2%80%93Fadings|Graphic]] on the data page. From this follows: | ||
| + | $${\rm Pr}(a \le 1) = \frac{1}{2} \cdot 0.35 \hspace{0.15cm} \underline{ \approx 17.5\,\%} \hspace{0.05cm}.$ | ||
| + | *This probability value will be a little too small because the red curve is concave in the range between $0$ and $1$. | ||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' The Gaussian approximation states that one can approximate the Rice distribution by a Gaussian distribution with mean $|z_0| = \sqrt{10} = 3.16$ and dispersion $\sigma = 1$ if the quotient $|z_0|/\sigma$ is sufficiently large. Then applies: | ||
| + | $${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -2.16) = {\rm Q}(2.16) \hspace{0.15cm} \underline{ \approx 1.5\,\%} \hspace{0.05cm}.$ | ||
| + | *Here $g$ denotes a Gaussian distributed random variable with the mean value $0$ and the dispersion $\sigma = 1$. | ||
| + | *The numerical value was determined with the specified interactive [[Applets:QFunction|Applet]]. | ||
| − | |||
| − | |||
| − | * | + | <i>Note:</i> The Gaussian approximation is certainly associated with a certain error here: |
| − | + | *From the graph you can see that the average value of the green curve is not $a = $3.16$, but rather $3.31$. | |
| + | *Then the power of the Gaussian approximation $(3.31^2 + 1^2 = 12)$ is exactly the same as that of the Rice distribution: | ||
| + | :$$|z_0|^2 + 2 \sigma^2= 10 + 2 =12\hspace{0.05cm}.$$ | ||
| − | + | '''(5)''' Using the same calculation method, replace the Rice–WDF with a Gauss–WDF with mean value $\sqrt{20} \approx $4.47 and spread $\sigma = $1 and you get | |
| − | + | $${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -3.37) = {\rm Q}(3.37) { \approx 0.04\,\%} \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| − | + | *If one assumes the equal power Gaussian distribution (see the note to the last subtask), the mean value is $m_g = \sqrt{21}\approx 4.58$, and the probability would then be | |
| − | + | $${\rm Pr}(a \le 1) \approx {\rm Q}(3.58) \hspace{0.15cm} \underline{ \approx 0.02\,\%} \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 11:48, 15 April 2020
As you can see in the diagram, we consider the same scenario as in Exercise 1.6:
- Rice fading with variance $\sigma^2 = 1$ the Gaussian processes and the parameter $|z_0|$ for the direct path.
- Regarding direct path, we are interested in the parameter values $|z_0|^2 = 0, \ 2, \ 4, \ 10, \ 20$ (see graphic).
- The WDF of the amount $a(t) = |z(t)|$ is
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}.$ * For example, the modified zero-order Bessel function returns the following values: $${\rm I }_0 (2) = 2.28\hspace{0.05cm},\hspace{0.2cm}{\rm I }_0 (4) = 11.30\hspace{0.05cm},\hspace{0.2cm}{\rm I }_0 (3) = 67.23
\hspace{0.05cm}.$$
* The quadratic expectation value ⇒ power of the multiplicative factor $|z(t)|$, is equal
$${\rm E}\left [ a^2 \right ] = {\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2
\hspace{0.05cm}.$$
* With $z_0 = 0$ the <i>Rice fading</i> becomes the more critical <i>Rayleigh fading</i>. In this case, the probability that $a$ lies in the yellow-shaded area between $0$ and $1$ applies:
$$$ {\rm Pr}(a \le 1) = 1 - {\rm e}^{-0.5/\sigma^2} \approx 0.4
\hspace{0.05cm}.'"`UNIQ-MathJax24-QINU`"'{\rm Pr}(a \le 1) = {1}/{2} \cdot f_a(a=1)
\hspace{0.05cm}.'"`UNIQ-MathJax25-QINU`"'f_a(a) = a \cdot {\rm exp} [ -\frac{a^2 + 4}{2}] \cdot {\rm I}_0 (2a)\hspace{0.05cm}.$
- This gives the values searched for:
- $$f_a(a = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \cdot {\rm e}^{-2.5} \cdot {\rm I}_0 (2) = 0.082 \cdot 2.28 \hspace{0.15cm} \underline{ = 0.187}\hspace{0.05cm},$$
- $$f_a(a = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm e}^{-4} \cdot {\rm I}_0 (4) = 2 \cdot 0.0183 \cdot 11.3 \hspace{0.15cm} \underline{ = 0.414}\hspace{0.05cm},$$
- $$f_a(a = 3) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \cdot {\rm e}^{-6.5} \cdot {\rm I}_0 (6) = 3 \cdot 0.0015 \cdot 67.23 \hspace{0.15cm} \underline{ = 0.303}\hspace{0.05cm}.$$
- The results fit well with the blue curve on the specifications page.
(2) With the result of the subtask (1) ⇒ $f_a(a = 1) = 0.187$ is obtained with the triangle approximation: $${\rm Pr}(a \le 1) = {1}/{2} \cdot 0.187 \cdot 1\hspace{0.15cm} \underline{ \approx 9.4\,\%} \hspace{0.05cm}.$$
- This result will be a bit too large, because the blue curve is below the connecting line from $(0, 0)$ to $(1, 0.187)$ ⇒ convex curve.
(3) For the red curve the WDF–value $f_a(a = 1) \approx 0.35$ can be read from the Graphic on the data page. From this follows: $${\rm Pr}(a \le 1) = \frac{1}{2} \cdot 0.35 \hspace{0.15cm} \underline{ \approx 17.5\,\%} \hspace{0.05cm}.$ *This probability value will be a little too small because the red curve is concave in the range between $0$ and $1$. '''(4)''' The Gaussian approximation states that one can approximate the Rice distribution by a Gaussian distribution with mean $|z_0| = \sqrt{10} = 3.16$ and dispersion $\sigma = 1$ if the quotient $|z_0|/\sigma$ is sufficiently large. Then applies: $${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -2.16) = {\rm Q}(2.16) \hspace{0.15cm} \underline{ \approx 1.5\,\%} \hspace{0.05cm}.$ *Here $g$ denotes a Gaussian distributed random variable with the mean value $0$ and the dispersion $\sigma = 1$. *The numerical value was determined with the specified interactive [[Applets:QFunction|Applet]]. <i>Note:</i> The Gaussian approximation is certainly associated with a certain error here: *From the graph you can see that the average value of the green curve is not $a = $3.16$, but rather $3.31$.
- Then the power of the Gaussian approximation $(3.31^2 + 1^2 = 12)$ is exactly the same as that of the Rice distribution:
- $$|z_0|^2 + 2 \sigma^2= 10 + 2 =12\hspace{0.05cm}.$$
(5) Using the same calculation method, replace the Rice–WDF with a Gauss–WDF with mean value $\sqrt{20} \approx $4.47 and spread $\sigma = $1 and you get
$${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -3.37) = {\rm Q}(3.37) { \approx 0.04\,\%} \hspace{0.05cm}.$$
- If one assumes the equal power Gaussian distribution (see the note to the last subtask), the mean value is $m_g = \sqrt{21}\approx 4.58$, and the probability would then be
$${\rm Pr}(a \le 1) \approx {\rm Q}(3.58) \hspace{0.15cm} \underline{ \approx 0.02\,\%} \hspace{0.05cm}.$$