Difference between revisions of "Aufgaben:Exercise 3.4: Trapezoidal Spectrum and Pulse"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=*Buch*/*Kapitel* }} ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"} - Falsch + Richtig {Input-Box Frage |…“) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=*Buch*/*Kapitel* | {{quiz-Header|Buchseite=*Buch*/*Kapitel* | ||
}} | }} | ||
| + | |||
| + | [[File:P_ID508__Sig_A_3_4.png|250px|right|Trapezspektrum und -impuls (Aufgabe A3.4)]] | ||
| + | |||
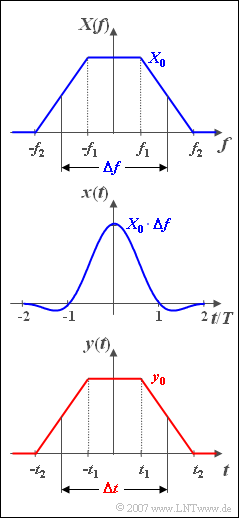
| + | Wir betrachten hier eine trapezförmige Spektralfunktion $X(f)$ gemäß der oberen Grafik, die durch die drei Parameter $X_0$, $f_1$ und $f_2$ vollständig beschrieben wird. Für die Eckfrequenzen gelte $f_2 > 0$ und $0 \geq f_1 \geq f_2$. | ||
| + | Anstelle der Eckfrequenzen $f_1$ und $f_2$ können auch die beiden folgenden Beschreibungsgrößen verwendet werden: | ||
| + | *die äquivalente Bandbreite: | ||
| + | $$\Delta f = f_1 + f_2,$$ | ||
| + | *der so genannte Rolloff-Faktor (im Frequenzbereich): | ||
| + | $$r_f = \frac{{f_2 - f_1 }}{{f_2 + f_1 }}.$$ | ||
| + | |||
| + | |||
| + | Mit diesen Größen lautet die dazugehörige Zeitfunktion (siehe Grafik in der Mitte): | ||
| + | |||
| + | $$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( {{\rm \pi} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( {{\rm \pi} \cdot r_f \cdot \Delta f\cdot t} ).$$ | ||
| + | |||
| + | Hierbei ist $\text{si}(x) = \text{sin}(x)/x$ die so genannte Spaltfunktion. | ||
| + | In diesem Beispiel sollen die Zahlenwerte $X_0 = 10^{–3}$ V/Hz, $f_1 = 1$ kHz und $f_2 = 3$ kHz verwendet werden. Die Zeit $T = 1/\Delta f$ dient lediglich zu Normierungszwecken. | ||
| + | |||
| + | Ab Aufgabe 3) wird ein trapezförmiges Signal $y(t)$ betrachtet, das formgleich mit dem Spektrum $X(f)$ ist. Als Beschreibungsgrößen können hier verwendet werden: | ||
| + | die Impulsamplitude $y_0 = y(t = 0)$, | ||
| + | die äquivalente Impulsdauer (definiert über das flächengleiche Rechteck): | ||
| + | |||
| + | $$\Delta t = t_1 + t_2,$$ | ||
| + | |||
| + | der Rolloff-Faktor (im Zeitbereich): | ||
| + | |||
| + | $$r_t = \frac{{t_2 - t_1 }}{{t_2 + t_1 }}.$$ | ||
| + | |||
| + | Es gelte $y_0 = 4$ V, $\Delta t = 1$ ms und $r_t = 0.5$. | ||
| + | |||
| + | |||
| + | Hinweis: Diese Aufgabe soll unter Verwendung von Vertauschungssatz und Ähnlichkeitssatz gelöst werden. Sie können Ihre Ergebnisse anhand zweier Interaktionsmodule überprüfen: | ||
| + | *Zeitfunktion und zugehörige Spektralfunktion | ||
| + | *Frequenzgang und zugehörige Impulsantwort | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Wie groß sind bei den gegebenen Parametern die äquivalente Bandbreite und der Rolloff-Faktor des Spektrums $X(f)$? | ||
| + | |type="{}"} | ||
| + | $\Delta f =$ { 4 } kHz | ||
| + | $r_f = { 0.5 } | ||
| − | { | + | {Wie groß sind die Signalwerte von $x(t)$ bei $t = 0$, $t = T/2$ und $t = T$? |
|type="{}"} | |type="{}"} | ||
| − | + | $x(t=0) =$ { 4 } V | |
| + | $x(t=T/2) =$ { 2.293 3% } V | ||
| + | $x(t=T) =$ { 0 } V | ||
| + | {Wie lautet das Spektrum $Y(f)$ des Trapezimpulses mit $y_0 = 4$ V, $\Delta t = 1$ ms, $r_t = 0.5$. Wie groß sind die Spektralwerte bei $f$ = 0, 500 Hz und 1 kHz? | ||
| + | |type="{}"} | ||
| + | $Y(f = 0) =$ { 4 } mV/kHz | ||
| + | $Y(f = 0.5 \text{kHz}) =$ { 2.293 3% } mV/Hz | ||
| + | $Y(f = 1 \text{kHz}) =$ { 0 } mV/Hz | ||
| + | {Welche Spektralwerte ergeben sich mit $y_0 = 8$ V, $\Delta t = 0.5$ ms und $r_t = 0.5$? | ||
| + | |type="{}"} | ||
| + | $Y(f=0) =$ { 4 } mV/Hz | ||
| + | $Y(f=1\text{kHz}) =$ { 2.293 3% } mV/Hz | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
| + | |||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Die äquivalente Bandbreite ist per Definition gleich der Breite des flächengleichen Rechtecks: |
| + | |||
| + | Für den Rolloff-Faktor gilt: | ||
| + | |||
| + | '''2.''' Der Maximalwert des Impulses $x(t)$ tritt zum Zeitpunkt $t = 0$ auf: $x_0 = X_0 \cdot \Delta f = 4$ V. | ||
| + | Zum Zeitpunkt $t = T = 1/\Delta f$ gilt aufgrund von $\text{si}(\pi) = 0$: | ||
| + | |||
| + | Auch bei allen Vielfachen von $T$ weist $x(t)$ Nulldurchgänge auf. Zum Zeitpunkt $t = T/2$ gilt: | ||
| + | |||
| + | '''3.''' Die zum trapezförmigen Spektrum $X(f)$ zugehörige Zeitfunktion lautet (siehe Angabe): | ||
| + | |||
| + | Da sowohl $X(f)$ als auch $x(t)$ reell sind und $y(t)$ formgleich mit $X(f)$ ist, erhält man unter Berücksichtigung aller Äquivalenzen für die Spektralfunktion des Trapezimpulses: | ||
| + | |||
| + | Insbesondere gilt: | ||
| + | |||
| + | |||
| + | |||
| + | '''4.''' Der Spektralwert bei der Frequenz $f = 0$ wird nicht verändert: $Y_0 = y_0 \cdot \Delta t = 4 \cdot 10^{–3}$ V/Hz. Da nun die Zeitfunktion nur halb so breit ist, verbreitert sich das Spektrum um den Faktor 2: | ||
| + | |||
| + | In der Teilaufgabe 3) ist dieser Spektralwert bei der Frequenz $f = 0.5$ kHz aufgetreten. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | ||
Revision as of 23:06, 17 April 2016
Wir betrachten hier eine trapezförmige Spektralfunktion $X(f)$ gemäß der oberen Grafik, die durch die drei Parameter $X_0$, $f_1$ und $f_2$ vollständig beschrieben wird. Für die Eckfrequenzen gelte $f_2 > 0$ und $0 \geq f_1 \geq f_2$. Anstelle der Eckfrequenzen $f_1$ und $f_2$ können auch die beiden folgenden Beschreibungsgrößen verwendet werden:
- die äquivalente Bandbreite:
$$\Delta f = f_1 + f_2,$$
- der so genannte Rolloff-Faktor (im Frequenzbereich):
$$r_f = \frac[[:Template:F 2 - f 1]][[:Template:F 2 + f 1]].$$
Mit diesen Größen lautet die dazugehörige Zeitfunktion (siehe Grafik in der Mitte):
$$x( t ) = X_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} ( {{\rm \pi} \cdot \Delta f \cdot t} ) \cdot {\mathop{\rm si}\nolimits} ( {{\rm \pi} \cdot r_f \cdot \Delta f\cdot t} ).$$
Hierbei ist $\text{si}(x) = \text{sin}(x)/x$ die so genannte Spaltfunktion. In diesem Beispiel sollen die Zahlenwerte $X_0 = 10^{–3}$ V/Hz, $f_1 = 1$ kHz und $f_2 = 3$ kHz verwendet werden. Die Zeit $T = 1/\Delta f$ dient lediglich zu Normierungszwecken.
Ab Aufgabe 3) wird ein trapezförmiges Signal $y(t)$ betrachtet, das formgleich mit dem Spektrum $X(f)$ ist. Als Beschreibungsgrößen können hier verwendet werden: die Impulsamplitude $y_0 = y(t = 0)$, die äquivalente Impulsdauer (definiert über das flächengleiche Rechteck):
$$\Delta t = t_1 + t_2,$$
der Rolloff-Faktor (im Zeitbereich):
$$r_t = \frac[[:Template:T 2 - t 1]][[:Template:T 2 + t 1]].$$
Es gelte $y_0 = 4$ V, $\Delta t = 1$ ms und $r_t = 0.5$.
Hinweis: Diese Aufgabe soll unter Verwendung von Vertauschungssatz und Ähnlichkeitssatz gelöst werden. Sie können Ihre Ergebnisse anhand zweier Interaktionsmodule überprüfen:
- Zeitfunktion und zugehörige Spektralfunktion
- Frequenzgang und zugehörige Impulsantwort
Fragebogen
Musterlösung
Für den Rolloff-Faktor gilt:
2. Der Maximalwert des Impulses $x(t)$ tritt zum Zeitpunkt $t = 0$ auf: $x_0 = X_0 \cdot \Delta f = 4$ V. Zum Zeitpunkt $t = T = 1/\Delta f$ gilt aufgrund von $\text{si}(\pi) = 0$:
Auch bei allen Vielfachen von $T$ weist $x(t)$ Nulldurchgänge auf. Zum Zeitpunkt $t = T/2$ gilt:
3. Die zum trapezförmigen Spektrum $X(f)$ zugehörige Zeitfunktion lautet (siehe Angabe):
Da sowohl $X(f)$ als auch $x(t)$ reell sind und $y(t)$ formgleich mit $X(f)$ ist, erhält man unter Berücksichtigung aller Äquivalenzen für die Spektralfunktion des Trapezimpulses:
Insbesondere gilt:
4. Der Spektralwert bei der Frequenz $f = 0$ wird nicht verändert: $Y_0 = y_0 \cdot \Delta t = 4 \cdot 10^{–3}$ V/Hz. Da nun die Zeitfunktion nur halb so breit ist, verbreitert sich das Spektrum um den Faktor 2:
In der Teilaufgabe 3) ist dieser Spektralwert bei der Frequenz $f = 0.5$ kHz aufgetreten.